 |
Join Techniques: Nested loop, Sort Merge, Hash based join |
| << Special Indexing Techniques: Inverted, Bit map, Cluster, Join indexes |
| Data mining (DM): Knowledge Discovery in Databases KDD >> |

Lecture-
28
Join
Techniques
Background
Used to
retrieve data from multiple
tables.
Joins
used frequently, hence lot of
work on improving or optimizing
them.
Simplest
join that works in most
cases is nested-loop join
but results in quadratic
time
complexity.
Tables
identified by FROM clause
and condition by WHERE clause.
Will
cover different types of
joins.
Join
commands are statements that
retrieve data from multiple
tables. A join is identified
by
multiple
tables in the FROM clause,
and the relationship between
the tables to be joined
is
established
through the existence of a
join condition in the WHERE clause.
Because joins are so
frequently
used in relational queries and
because joins are so expensive,
lot of effort has gone
into
developing
efficient join algorithms and
techniques. The simplest
i.e. nested-loop join
is
applicable in
all cases, but results in
quadratic performance. Several fast
join algorithms have
been developed
and extensively used; these
can be categorized as sort
-merge, hash-based,
and
index-based
algorithms. In this lecture we will be
covering the following
join
algorithms/techniques:
�
Nested loop
join
�
Sort
Merge Join
�
Hash
based join
�
Etc.
About
Nested-Loop Join
Typically
used in OLTP
environment.
Limited
application for DSS and
VLDB
In DSS
environment we deal with
VLDB and large sets of
data.
Traditionally
Nested -Loop join has
been and is used in OLTP
environments, but for many
reasons,
such a join mechanism is not
suitable for VLDB and
DSS environments. Nested
loop
joins
are useful when small
subsets of data are joined
and if the join condition is
an efficient way
of accessing
the inner table. Despite
these restrictions/limitations, we will begin
our discussion
with
the traditional join
technique i.e. nested loop
join, so that you can
appreciate the benefits of
the
join techniques typically used in a
VLDB and DSS
environment.
226

Nested-Loop
Join: Code
FOR i = 1 to n DO
BEGIN
/*
N rows in
T1
*/
IF ith
row of T1 qualifies THEN
BEGIN
For j = 1 to m
DO BEGIN
/*
M rows in
T2
*/
IF the
ith row of T1 matches to jth
row of T2 on join key THEN
BEGIN
IF the
jth row of T2 qualifies THEN
BEGIN
produce output
row
END
END
END
END
END
Nested loop
join wo rks like a nested
loop used in a high level
programming language, where each
value of
the index of the outer loop is
taken as a limit (or
starting point or whatever
applicable)
for
the index of the inner loop,
and corresponding actions are
performed on the
statement(s)
following
the inner loop. So basically, if
the outer loop executes R
times and for each
such
execution
the inner loop executes S
times, then the total cost
or time complexity of the nested
loop is
O(RS).
Nested-loop joins
provide efficient access when
tables are indexed on join
columns. Furthermore,
in many
small transactions, such as
those affecting only a small
set of rows, index nested
loops
joins are
far superior to both sort -merge joins
and hash joins. A nested
loop join involves
the
following
steps:
1. The optimizer
determines the major table
(i.e. Table_A) and
designates it as the
outer
table.
Table_A
is
accessed once. If the outer
table has no useful indexes, a
full table scan
is performed. If an index
can reduce I/O costs,
the index is used to locate
the rows.
2. The other
table is designated as the
inner table or Table_B. Table_B
is
accessed once for
each
qualifying row (or touple) in
Table_A.
3. For
every row in the outer
table, DBMS accesses all
the rows in the inner
table. The outer
loop is
for every row in outer
table and the inner
loop is for every row in
the inner table.
If 10 rows from
Table_A
match
the conditions in the query,
Table_B
is
accessed 10 times. If
Table_B
has a
useful index on the join
column, it might require 5 I/Os to
read the data block
for
each
scan, plus one I/O
for each data block. Hence
the total cost of accessing
Table_B
would
be
60 logical
I/Os.
227
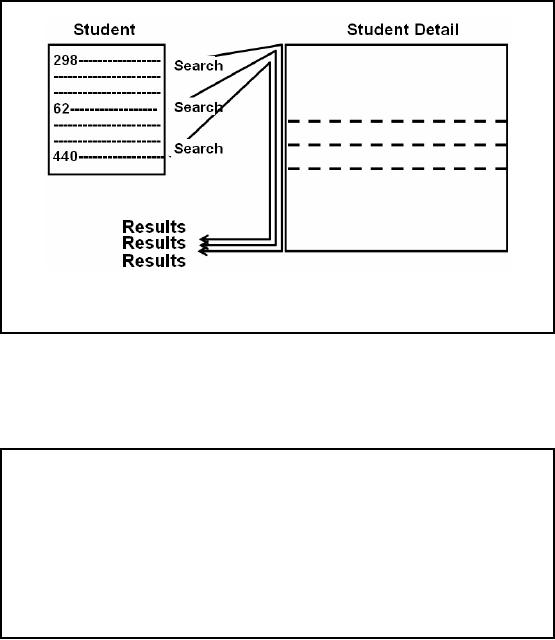
Nested-Loop
Join: Working Example
For each
qualifying row of Personal
table,
Academic
table is examined for
matching rows.
Figure-28.1:
The process of Nested-Loop
Join without
indexing
The
process of creating the result
set for a nested-loop join
is achieved by nesting the tables,
and
scanning
the inner table repeatedly
for each qualifying row of
the outer table. This
process is
shown in Figure-28.1:
The question being asked is
"What is
the average GPS of
undergraduate
male
students?".
Nested-Loop
Join: Order of
Tables
If the outer
loop executes R times and
the inner loop executes S
times, then the time
complexity
will be
O(RS).
The
time complexity should be independent of
the order of tables i.e. O(RS) is
same as O(SR).
However, in
the context of I/Os the
order of tables does
matter.
Along
with this the relationship
between the number of
qualifyin g rows/blocks between
the two
tables
matters.
It is true that
the actual number of matching rows
returned as a result of the join
would be
independent of
the order of tables i.e.
inner or outer; actually it is
going to be even independent of
the
type of join used. Now
assume that depending on the
filter criterion, different number of
rows
is returned from
the two tables to be joined.
Let the rows returned from
Table_A be RA
and
rows
returned
from Table_B be RB, and
let R A < RB. If
Table_B would have been
the outer table, then
for
each row returned, the
inner table i.e. Table_A
would have been scanned
(assuming no
indexing)
RB times. However, if
Table_A would have been the
outer table, then for
each row
returned,
the inner table i.e.
Table_B would have been
scanned (assuming no indexing)
RA times
228

i.e.
less number of times scanned. Meaning,
even if the inner table
have fewer number of
qualifying rows,
it is going to be scanned the number of
times the qualifying rows of
the outer
table.
Hence the choice of tables
does matter.
Nested-Loop
Join: Cost Formula
Join cost =
Cost of accessing Table_A
+
# of qualifying
rows in Table_A
�
Blocks of
Table_B
to be
scanned for each qualifying
row
OR
Join cost =
Blocks accessed for Table_A
+
Blocks
accessed for Table_A
�
Blocks
accessed for Table_B
For a
high level programming
language, the time complexity of a nested
-loop join remains
unchanged if
the order of the loops
are changed i.e. the
inner and outer loops are
interchanged.
However,
this is NOT true for
Nested-Loop-Joins in the context of
DSS when we look at the
I/O.
For a
nested-loop join with two
tables, the formula for
estimating the join cost
is:
Join cost =
Cost of accessing Table_A
+
# of qualifying
rows in Table_A
�
Blocks of
Table_B
to be
scanned for each qualifying
row.
OR
Join cost =
Blocks accessed for Table_A
+
Blocks
accessed for Table_A
�
Blocks
accessed for Table_B
For a
Nested-Loop join inner and outer
tables are determined as
follows:
The outer
table is usually the one
that has:
The
smallest number of qualifying rows,
and/or
�
The
largest numbers of I/Os required to
locate the rows.
�
The inner
table usually has:
The
largest number of qualifying rows,
and/or
�
The
smallest number of reads required to
locate rows.
229

Nested-Loop
Join: Cost of reorder
Table_A = 500
blocks and
Table_B = 700
blocks.
Qualifying
blocks for Table_A
QB(A) = 50
Qualifying
blocks for Table_B
QB(B) =
100
Join
cost A&B = 500 + 50� 700 =
35,500 I/Os
Join
cost B&A = 700 + 100� 500 = 50,700
I/Os
i.e. an increase
in I/O of about 43%.
For
example, if qualifying blocks
for Table_A
QB(A) = 50
and qualifying blocks for
Table_B
QB(B) = 100
and size of Table_A is 500
blocks and size of Table_B
is 700 blocks then Join
cost
A&B = 500 +
50�
700 =
35,500 I/Os and using the
other order i.e. Table_B
outer
table and
Table_A
as
inner table, the join
cost B&A = 700 + 100� 500 =
50,700 I/Os i.e. an increase
in I/O
of about
43%.
Nested-Loop
Join: Variants
1. Naive
nested-loop join
2. Index
nested-loop join
3. Temporary index
nested-loop join
Working of Query
optimizer
There
are many variants of the
traditional nested-loop join.
The simplest case is when an
entire
table is
scanned; this is called a
naive nested -loop join. If
there is an index, and that
index is
exploited, then
it is called an index nested-loop join.
If the index is built as part of
the query plan
and
subsequently dropped, it is called as a temporary index
nested -loop join. All
these variants
are
considered by the query optimizer before
selecting the most
appropriate join
algorithm/technique.
Sort-Merge
Join
Joined tables to
be sorted as per WHERE clause of
the join predicate.
Query optimizer
scans for (cluster) index,
if exists performs join.
In the
absence of index, tables are
sorted on the columns as per
WHERE clause.
If multiple
equalities in WHERE clause,
some merge columns
used.
230
The Sort
-Merge join requires that
both tables to be joined are
sorted on those columns that
are
identified by
the equality in the WHERE clause of
the join predicate.
Subsequently the tables
are
merged
based on the join columns.
The query optimizer typically scans an index on
the columns
which
are part of the join, if
one exists on the proper set
of columns, fine, else the
tables are
sorted on
the columns to be joined ,
resulting in what is called a cluster
index. However, in
rare
cases,
there may be multiple
equalities in the WHERE clause, in
such a case, the merge
columns
are
taken from only some of
the given equality
clauses.
Because
each table is sorted, the
Sort -Merge Join operator
gets a row from each
table and
compares it
one at a time with the rows
of the other table. For
example, for equi-join
operations,
the rows
are returned if they
match/equal on the join
predicate. If they are not
equal or don't
match,
whic hever row has
the lower value is
discarded, and next row is
obtained from that
table.
This
process is repeated until
all the rows have been
exhausted.
The Sort
-Merge join process just
described works as follows:
� Sort
Table_A
and
Table_B
on
the join column in ascending
order, then scan them to do
a
``merge''
(on join column), and output
result tuples/rows.
Proceed
with scanning of Table_A
until current
A_tuple ≤ current B_tuple,
then
�
proceed
scanning of Table_B
until
current B_tuple ≤ current A_tuple;
do this
until current
A_tuple = current B_tuple.
�
At this point,
all A_tuples with same value
in Ai (current A_group) and
all
B_tuples
with same value in Bj (current
B_group) match; output
<a, b> for all
pairs of
such tuples/records.
�
Update pointers,
resume scanning Table_A
and
Table_B
.
� Table_A
is
scanned once; each B group
is scanned once per matching
Table_A
tuple.
(Multiple
scans of a B group are
likely to find needed pages
in buffer.)
� Cost: M
log M + N log N +
(M+N)
� The
cost of scanning is M+N,
could be M*N (very
unlikely!)
231

Figure-28.2:
The process of
merging
Fig-28.2
shows the process of merging
two sorted tables with
IDs shown. Conceptually
the
merging is
similar to the merging you must
have studies in Merge_Sort in your
Algorithm course.
Sort-Merge
Join: Note
Very
fast.
Sorting can be
expensive.
Presorted
data can be obtained from
existing B-tree.
Sort-Merge join
itself is very fast, but it
can be an expensive choice if
sort operations are
required
frequently
i.e. the contents of the t
able's change often resulting in deterioration of
the sort order.
However, it
may so happen that even if
the data volume is large the
desired data can be
obtained
presorted
from existing B-tree. For
such a case sort -merge
join is often the fastest
availabl e join
algorithm.
Hash-Based
Join: Working
Suitable
for the VLDB
environment.
The
choice which table first
gets hashed plays a pivotal
role in the overall performance of
the join
operation, this
decided by the optimizer.
The joined
rows are identified by collisions i.e.
collisions are "good" in case of
hash join.
232
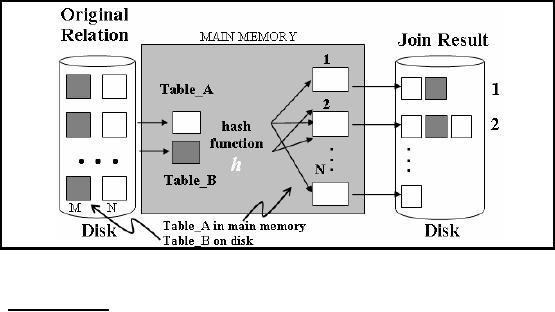
Hash joins
are suitable for the
VLDB environment as they are
useful for joining large data
sets or
tables.
The choice about which
table first gets hashed
plays a pivotal role in the
overall
performance of
the join operation, and
left to the optimizer. The optimizer
decides by using the
smaller of the
two tables (say) Table_A
or
data sources to build a hash
table in the main memory
on the
join key used in the
WHERE
clause. It
then scans the larger table
(say) Table_B
and
probes
the
hashed table to find the
joined rows. The joined rows
are identified by collisions i.e.
collisions
are
"good" in case of hash
join.
The optimizer
uses a hash join to join
two tables if they are
joined using an equij oin
and if either
of the
following conditions are
true:
A large amount
of data needs to be joined.
�
A large portion
of the table needs to be
joined.
�
This
method is best used when
the smaller table fits in
the available main memory.
The cost is
then
limited to a single read pass
over the data for
the two tables. Else
the "smaller" table has
to
be partitioned
which results in unnecessary
delays and degradation of performance due
to
undesirable
I/Os.
Figure-28.3:
Working of Hash-based join
Cost of
Hash -Join
� In partitioning
phase, read + write both
operations requires 2(M+N)
I/Os.
� In matching
phase, read both requires
M+N I/Os.
233

Hash-Based
Join: Large "small"
Table
Smaller of
the two tables may
grow too big to fit
into the main memory.
Optimizer performs
partitioning, but is not simple.
Multi-step
approach followed, each step
has a build phase and probe
phase.
Both tables
entirely consumed and partitioned via
hashing.
Hashing
guarantees any two joining
records will fall in same
pair of partitions.
Task
reduced to multiple, but smaller,
instances of the same
tasks.
It may so
happen that the smaller of
the two tables grows too big
to fit into the main
memory,
then
the optimizer breaks it up by
partitioning, such that a partition
can fit in the main
memory.
However, it is
not that simple because the
qualifying rows of both the tables
have to fall in the
corresponding
partition pairs that are
hashed (build) and probed.
Thus in such a case the hash
join
proceeds in
several steps. Each step has
a build phase and probe
phase. Initially, the two
tables
are entirely
consumed and partitioned (using a hash
function on the hash keys)
into multiple
partitions.
The number of such partitions is
sometimes called the
partitioning fan -out. Using
the
hash
function on the hash keys
(based on the predicates in
the WHERE clause)
guarantees that any
two
joining records must be in
the same pair of partitions.
Therefore, the task of
joining two large
tables
gets reduced to multiple, but
smaller, instances of the
same tasks. The hash
join is then
applied to each
pair of partitions.
Hash-Based
Join: Partition Skew
Partition
skew can
become a problem.
Hashing works under
the assumption of uniformity of
data distribution, may not be always
true.
Consequently
hash-based join degrades
into nested-loop
join.
Solution: Make
available other hash functions to be
chosen by the optimizer; that
better distribute
the
input.
Partition
skew can
become a problem in hash-join. In
the first step of hash
join, records are
hashed
into the main memory into
their corresponding bucket.
This being done based on the
hash
function
used. However, an attribute being hashed
may not be uniformly distributed within
the
relation,
and some buckets may
then contain more records than
other buckets. When
this
difference
becomes large, the corresponding bucket
may no longer fit in the
main memory. As a
consequence,
hash -based join degrades
into performance of a nested-loop join.
The only possible
solution is to
make available other hash functions to be
chosen by the optimizer; that
better
distribute the
input.
234

Hash-Based
Join: Intrinsic
Skew
Intrinsic
skew can
become a problem for hash, as
well as sort -merge
join.
The
skew is in data, NOT due to
hash function.
Example:
Many non-CS majors
registering for CS-101
instead of CS students in
summer.
Intrinsic
skew occurs when
attributes are not distributed uniformly;
it is also called attribute
value
skew.
For example a basic Computer
Science (CS) course being
offered in summer, and taken
by
many non
-CS majors who want to know
about computers. The course
taken by few
CS-majors
who
missed it or got an incomplete (i.e. I)
grade during the regular
semester due to one reason
or
another.
Ironically, intrinsic skew effects
the performance of both hash
and sort -merge
joins.
Sort-merge join
works best when the join
attributes are the primary
key of both tables.
This
property
guarantees absence of duplicates, so
that a record in the left
-hand-side of the relation
will
join with at most one record
in the right -hand-side of
the relation, thus avoiding
the intrinsic
skew.
235
Table of Contents:
- Need of Data Warehousing
- Why a DWH, Warehousing
- The Basic Concept of Data Warehousing
- Classical SDLC and DWH SDLC, CLDS, Online Transaction Processing
- Types of Data Warehouses: Financial, Telecommunication, Insurance, Human Resource
- Normalization: Anomalies, 1NF, 2NF, INSERT, UPDATE, DELETE
- De-Normalization: Balance between Normalization and De-Normalization
- DeNormalization Techniques: Splitting Tables, Horizontal splitting, Vertical Splitting, Pre-Joining Tables, Adding Redundant Columns, Derived Attributes
- Issues of De-Normalization: Storage, Performance, Maintenance, Ease-of-use
- Online Analytical Processing OLAP: DWH and OLAP, OLTP
- OLAP Implementations: MOLAP, ROLAP, HOLAP, DOLAP
- ROLAP: Relational Database, ROLAP cube, Issues
- Dimensional Modeling DM: ER modeling, The Paradox, ER vs. DM,
- Process of Dimensional Modeling: Four Step: Choose Business Process, Grain, Facts, Dimensions
- Issues of Dimensional Modeling: Additive vs Non-Additive facts, Classification of Aggregation Functions
- Extract Transform Load ETL: ETL Cycle, Processing, Data Extraction, Data Transformation
- Issues of ETL: Diversity in source systems and platforms
- Issues of ETL: legacy data, Web scrapping, data quality, ETL vs ELT
- ETL Detail: Data Cleansing: data scrubbing, Dirty Data, Lexical Errors, Irregularities, Integrity Constraint Violation, Duplication
- Data Duplication Elimination and BSN Method: Record linkage, Merge, purge, Entity reconciliation, List washing and data cleansing
- Introduction to Data Quality Management: Intrinsic, Realistic, Orr’s Laws of Data Quality, TQM
- DQM: Quantifying Data Quality: Free-of-error, Completeness, Consistency, Ratios
- Total DQM: TDQM in a DWH, Data Quality Management Process
- Need for Speed: Parallelism: Scalability, Terminology, Parallelization OLTP Vs DSS
- Need for Speed: Hardware Techniques: Data Parallelism Concept
- Conventional Indexing Techniques: Concept, Goals, Dense Index, Sparse Index
- Special Indexing Techniques: Inverted, Bit map, Cluster, Join indexes
- Join Techniques: Nested loop, Sort Merge, Hash based join
- Data mining (DM): Knowledge Discovery in Databases KDD
- Data Mining: CLASSIFICATION, ESTIMATION, PREDICTION, CLUSTERING,
- Data Structures, types of Data Mining, Min-Max Distance, One-way, K-Means Clustering
- DWH Lifecycle: Data-Driven, Goal-Driven, User-Driven Methodologies
- DWH Implementation: Goal Driven Approach
- DWH Implementation: Goal Driven Approach
- DWH Life Cycle: Pitfalls, Mistakes, Tips
- Course Project
- Contents of Project Reports
- Case Study: Agri-Data Warehouse
- Web Warehousing: Drawbacks of traditional web sear ches, web search, Web traffic record: Log files
- Web Warehousing: Issues, Time-contiguous Log Entries, Transient Cookies, SSL, session ID Ping-pong, Persistent Cookies
- Data Transfer Service (DTS)
- Lab Data Set: Multi -Campus University
- Extracting Data Using Wizard
- Data Profiling