QUALITY IMPROVEMENT TOOLS:Data Tables, Identify the problem, Random method

<< CUSTOMER FOCUSED PROJECT MANAGEMENT:Threshold Attributes

PROJECT EFFECTIVENESS THROUGH ENHANCED PRODUCTIVITY:Messages of Productivity, Productivity Improvement >>

Project Management MGMT627

LESSON 38

QUALITY IMPROVEMENT TOOLS

BROAD CONTENTS

Seven Basic Tools of Statistical Process Control

38.1

Seven Basic Tools of Statistical Process Control (SPC):

They are as follows:

1. Data Tables

2. Cause-and Effect Analysis

3. Histograms

4. Pareto Analysis

5. Scatter Diagrams

6. Trend Analysis

7. Process Control Charts

Quality Improvement Tools:

Over the years, statistical methods have become prevalent throughout business, industry, and

science. With the availability of advanced, automated systems that collect, tabulate, and analyze

data; the practical application of these quantitative methods continues to grow. Statistics today

plays a major role in all phases of modern business.

More important than the quantitative methods themselves is their impact on the basic

philosophy of business. The statistical point of view takes decision making out of the subjective

autocratic decision-making arena by providing the basis for objective decisions based on

quantifiable facts.

This change provides some very specific benefits:

Improved process information

Better communication

Discussion based on facts

Consensus for action

Information for process changes

Statistical Process Control (SPC) takes advantage of the natural characteristics of any process.

All business activities can be described as specific processes with known tolerances and

measurable variances. The measurement of these variances and the resulting information

provide the basis for continuous process improvement. The tools presented here provide both a

graphical and measured representation of process data. The systematic application of these tools

empowers business people to control products and processes to become world-class

competitors.

The basic tools of statistical process control are data figures, Pareto analysis, cause-and-effect

analysis, trend analysis, histograms, scatter diagrams, and process control charts. These basic

tools provide for the efficient collection of data, identification of patterns in the data, and

measurement of variability.

281

Project Management MGMT627

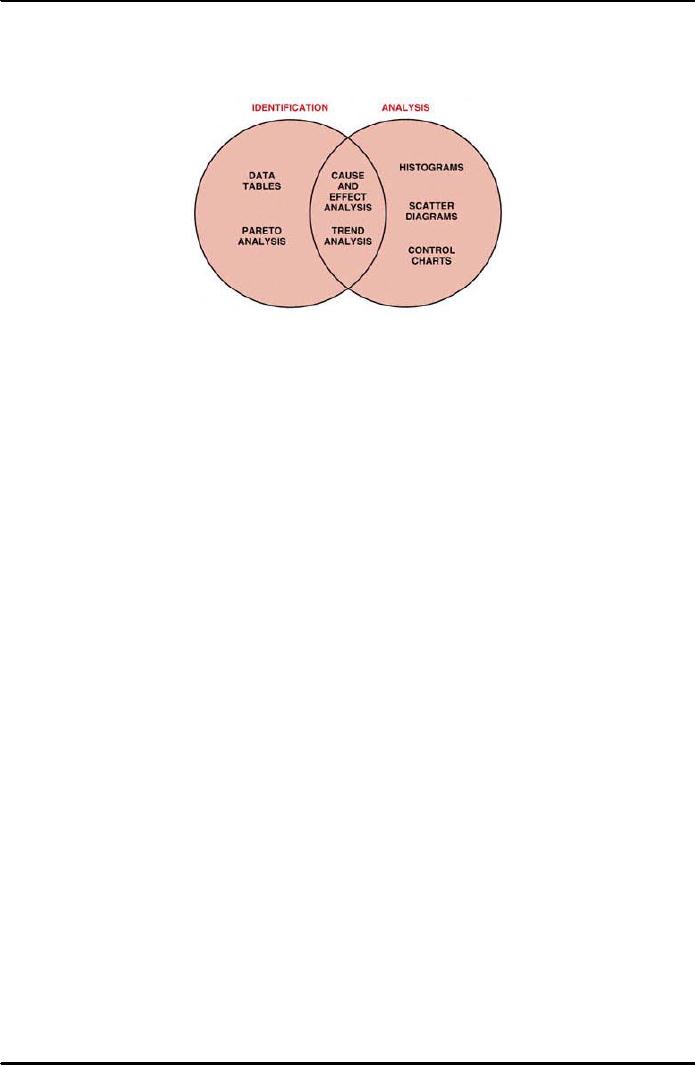
The following Figure 38.1 shows the relationships among these seven tools and their use for the

identification and analysis of improvement opportunities. We will review these tools and

discuss their implementation and applications.

Figure 38.1: Seven Quality Improvement Tools

38.1.1 Data Tables:

Data tables or data arrays provide a systematic method for collecting and displaying

data. In most cases, data tables are forms designed for the purpose of collecting specific

data. These tables are used most frequently where data is available from automated

media. They provide a consistent, effective, and economical approach to gathering data,

organizing them for analysis, and displaying them for preliminary review. Data tables

sometimes take the form of manual check sheets where automated data are not

necessary or available. Data figures and check sheets should be designed to minimize

the need for complicated entries. Simple-to-understand, straightforward tables are a key

to successful data gathering.

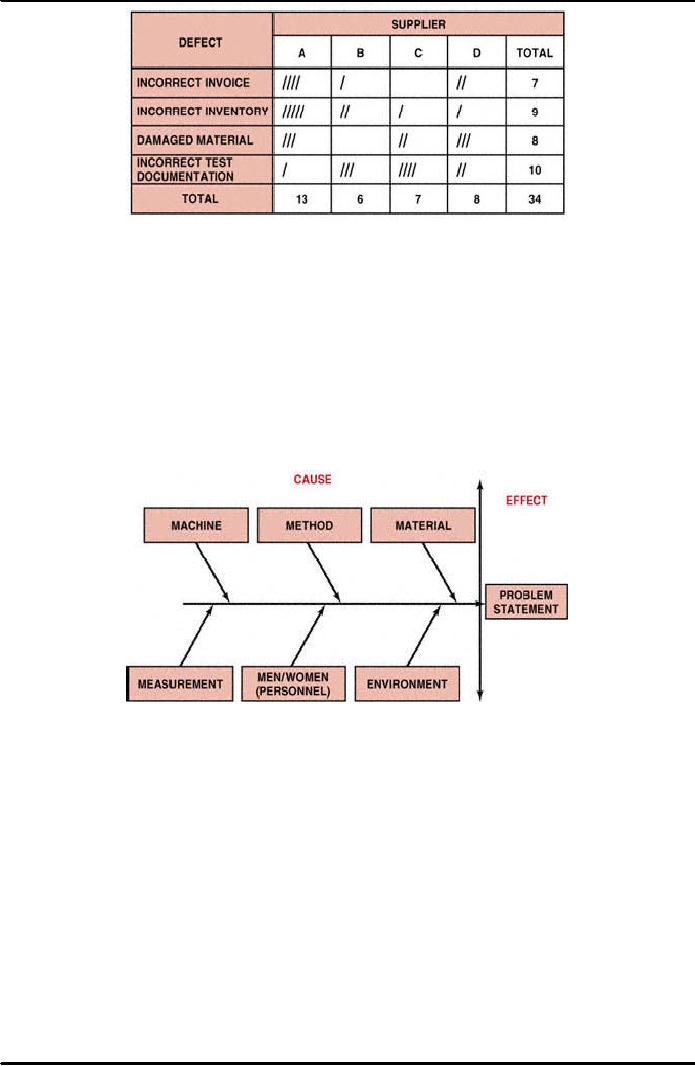
Figure 38.2 is an example of an attribute (pass/fail) data figure for the correctness of

invoices. From this simple check sheet several data points become apparent. The total

number of defects is 34. The highest number of defects is from supplier A, and the most

frequent defect is incorrect test documentation. We can subject this data to further

analysis by using Pareto analysis, control charts, and other statistical tools.

In this check sheet, the categories represent defects found during the material receipt

and inspection function. The following defect categories provide an explanation of the

check sheet:

Incorrect invoices: The invoice does not match the purchase order.

Incorrect inventory: The inventory of the material does not match the invoice.

Damaged material: The material received was damaged and rejected.

Incorrect test documentation: The required supplier test certificate was not received

and the material was rejected.

282

Project Management MGMT627

Figure 38.2: Check Sheet for "Material Receipt and Inspection"

38.1.2 Cause-and -Effect Analysis (C and EA) "Fishbone":

After identifying a problem, it is necessary to determine its cause. The cause-and-effect

relationship is at times obscure. A considerable amount of analysis often is required to

determine the specific cause or causes of the problem.

Cause-and-effect analysis uses diagramming techniques to identify the relationship

between an effect and its causes. Cause-and-effect diagrams are also known as

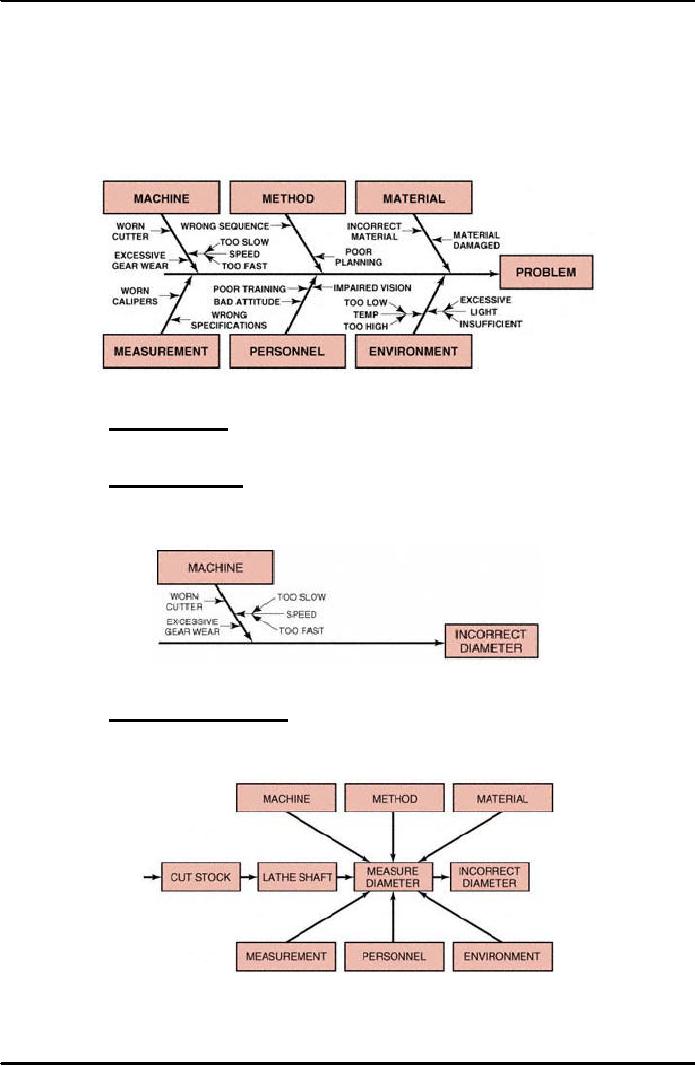
fishbone diagrams. Figure 38.3 demonstrates the basic fishbone diagram. Six steps are

used to perform a cause-and-effect analysis.

Figure 38.3: Cause-and-Effect Diagram

Step 1 Identify the problem:

This step often involves the use of other statistical process control tools, such as Pareto

analysis, histograms, and control charts, as well as brainstorming. The result is a clear,

concise problem statement.

Step 2 Select interdisciplinary brainstorming team:

Select an interdisciplinary team, based on the technical, analytical, and management

knowledge required determining the causes of the problem.

Step 3 Draw problem box and prime arrow:

The problem contains the problem statement being evaluated for cause and effect. The

prime arrow functions as the foundation for their major categories.

Step 4 Specify major categories:

Identify the major categories contributing to the problem stated in the problem box. The

six basic categories for the primary causes of the problems are most frequently

283

Project Management MGMT627

personnel, method, materials, machinery, measurements, and environment, as shown in

Figure 38.3. Other categories may be specified, based on the needs of the analysis.

Step 5 Identify defect causes:

When you have identified the major causes contributing to the problem, you can

determine the causes related to each of the major categories. There are three approaches

to this analysis: the random method, the systematic method, and the process analysis

method.

Figure 38.4: Random Method

Random method: List all six major causes contributing to the problem at the same time.

Identify the possible causes related to each of the categories, as shown in Figure 38.4.

Systematic method: Focus your analysis on one major category at a time, in descending

order of importance. Move to the next most important category only after completing

the most important one. This process is diagrammed in Figure 38.5.

Figure 38.5: Systematic Method

Process analysis method: Identify each sequential step in the process and perform

cause-and-effect analysis for each step, one at a time. Figure 38.6 represents this

approach.

Figure 38.6: Process Analysis Methods

284

Project Management MGMT627

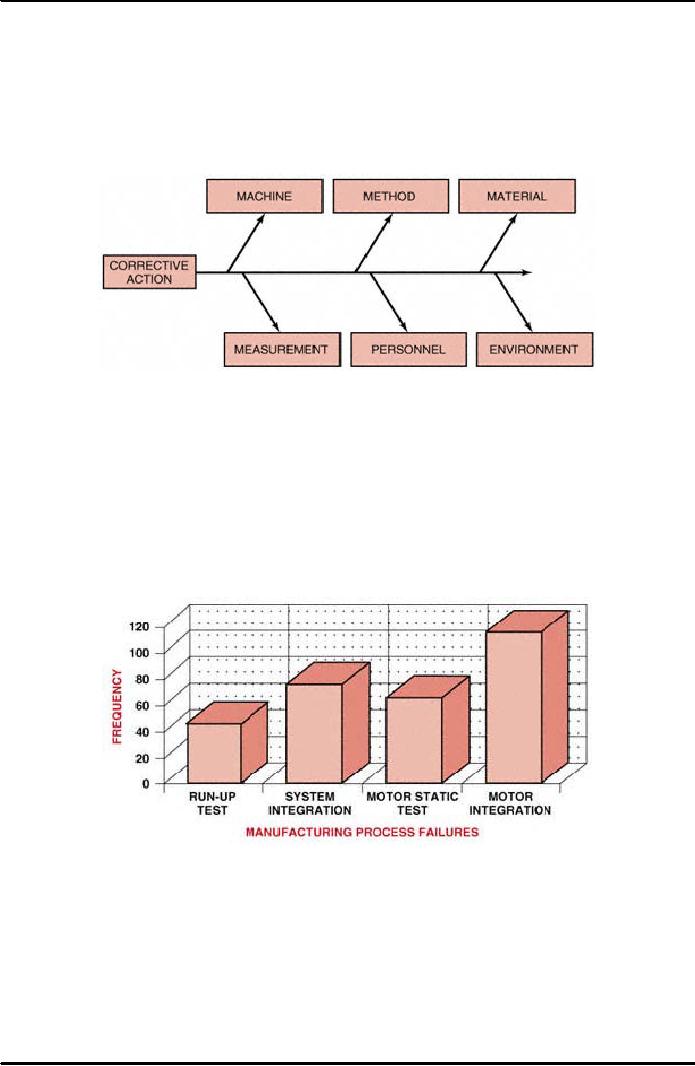
Step 6 Identify corrective action:

Based on (1) the cause-and-effect analysis of the problem and (2) the determination of

causes contributing to each major category, identify corrective action.

The corrective action analysis is performed in the same manner as the cause-and-effect

analysis. The cause-and-effect diagram is simply reversed so that the problem box

becomes the corrective action box. Figure 38.7 displays the method for identifying

corrective action.

Figure 38.7: Identify Corrective Action

38.1.3 Histogram-(HG):

A histogram is a graphical representation of data as a frequency distribution. This tool

is valuable in evaluating both attribute (pass/fail) and variable (measurement) data.

Histograms offer a quick look at the data at a single point in time; they do not display

variance or trends over time. A histogram displays how the cumulative data looks

today. It is useful in understanding the relative frequencies (percentages) or frequency

(numbers) of the data and how that data are distributed. Figure 38.8 illustrates a

histogram of the frequency of defects in a manufacturing process.

Figure 38.8: Histogram for Variables

38.1.4 Pareto Analysis (PA):

A Pareto diagram is a special type of histogram that helps us to identify and prioritize

problem areas. The construction of a Pareto diagram may involve data collected from

data figures, maintenance data, repair data, parts scrap rates, or other sources. By

identifying types of nonconformity from any of these data sources, the Pareto diagram

directs attention to the most frequently occurring element.

285

Project Management MGMT627

There are three uses and types of Pareto analysis:

1. The basic Pareto analysis identifies the vital few contributors that account for most

quality problems in any system.

2. The comparative Pareto analysis focuses on any number of program options or

actions.

3. The weighted Pareto analysis gives a measure of significance to factors that may

not appear significant at first-- such additional factors as cost, time, and criticality.

The basic Pareto analysis chart provides an evaluation of the most frequent occurrences

for any given data set. By applying the Pareto analysis steps to the material receipt and

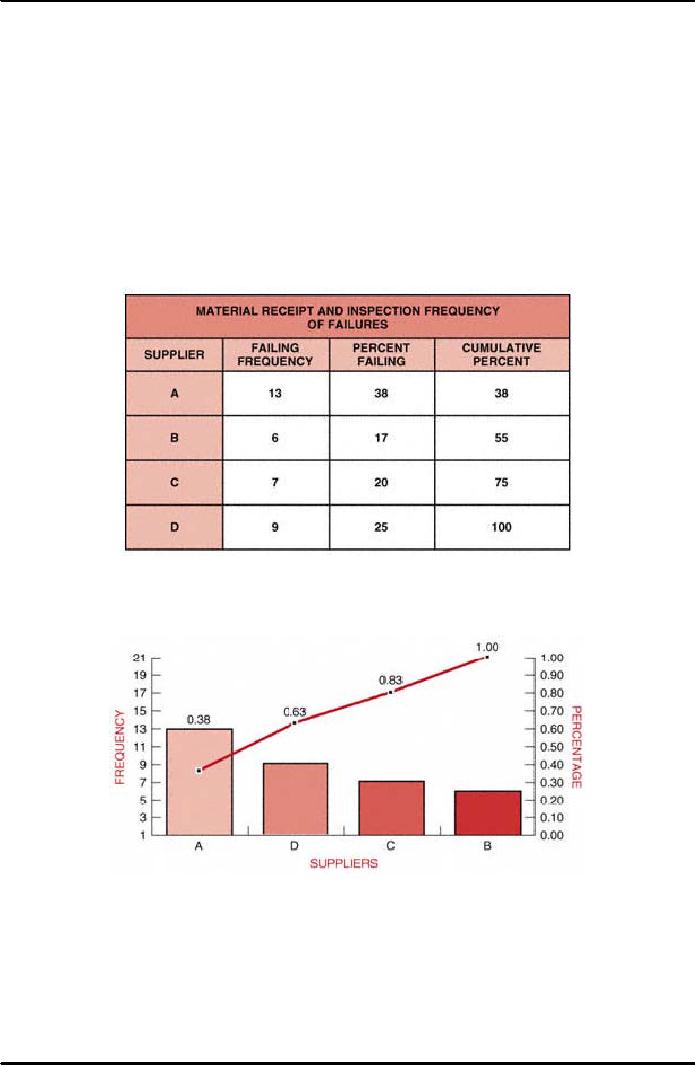
inspection process described in Figure 38.9, we can produce the basic Pareto analysis

demonstrated in Figure 38.10. This basic Pareto analysis quantifies and graphs the

frequency of occurrence for material receipt and inspection and further identifies the

most significant, based on frequency.

Figure 38.9: Material Receipt and Inspection Frequency of Failures

Figure 38.10: Basic Pareto Analysis

A review of this basic Pareto analysis for frequency of occurrences indicates that

supplier A is experiencing the most rejections with 37 percent of all the failures.

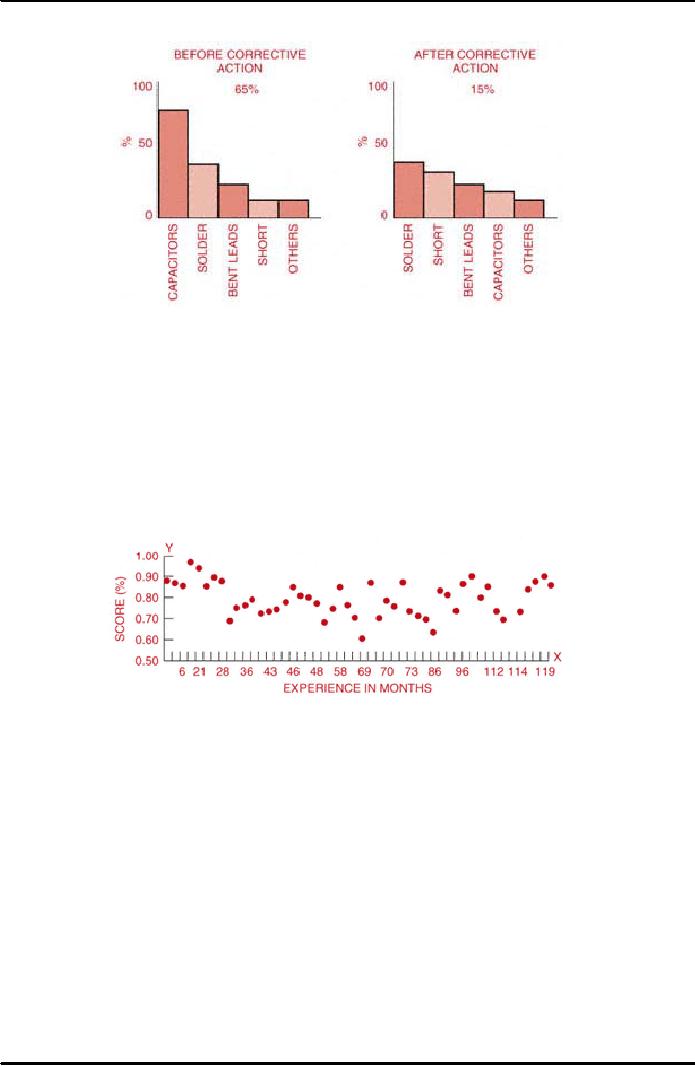
Pareto analysis diagrams are also used to determine the effect of corrective action, or to

analyze the difference between two or more processes and methods. Figure 38.11

286

Project Management MGMT627

displays the use of this Pareto method to assess the difference in defects after corrective

action.

Figure 38.11: Comparative Pareto Analysis

38.1.5 Scatter Diagrams:

Another pictorial representation of process control data is the scatter plot or scatter

diagram. A scatter diagram organizes data using two variables: an independent variable

and a dependent variable. These data are then recorded on a simple graph with X and Y

coordinates showing the relationship between the variables. Figure 38.12 displays the

relationship between two of the data elements from solder qualification test scores. The

independent variable, experience in months, is listed on the X-axis. The dependent

variable is the score, which is recorded on the Y-axis.

Figure 38.12: Solder Certification Test Score

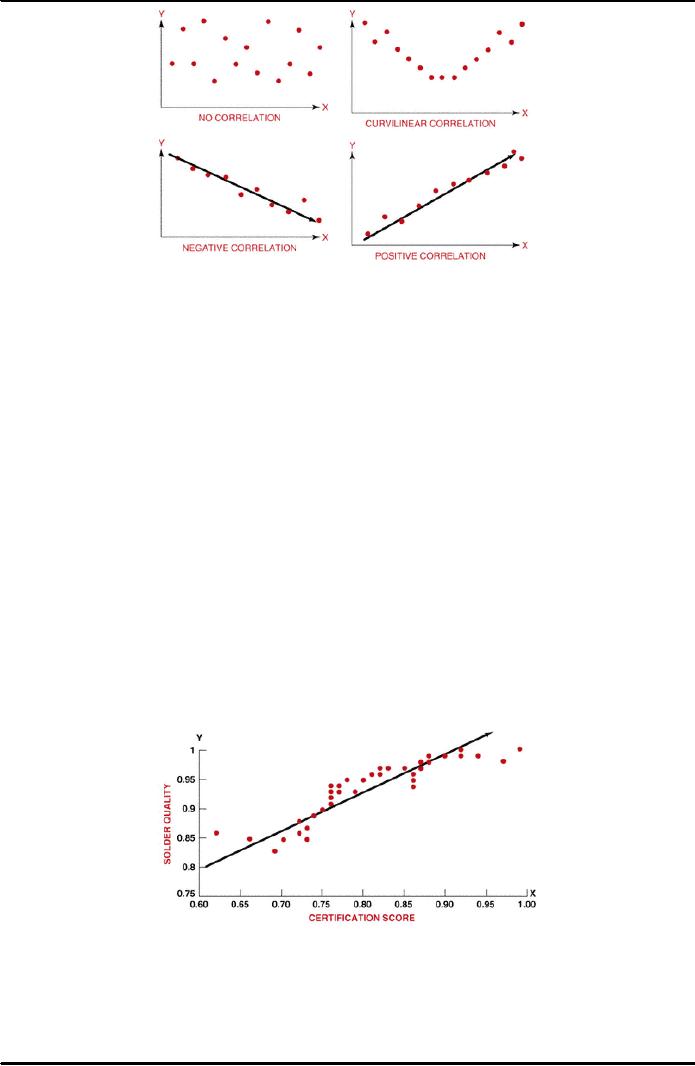
These relationships fall into several categories, as shown in Figure 38.13 below. In the

first scatter plot there is no correlation-- the data points are widely scattered with no

apparent pattern.

287

Project Management MGMT627

Figure 38.13: Scatter Plot Correlation

The second scatter plot shows a curvilinear correlation demonstrated by the U shape

of the graph. The third scatter plot has a negative correlation, as indicated by the

downward slope. The final scatter plot has a positive correlation with an upward

slope.

From Figure 38.12 we can see that the scatter plot for solder certification testing is

somewhat curvilinear. The least and the most experienced employees scored highest,

whereas those with an intermediate level of experience did relatively poorly. The next

tool, trend analysis, will help clarify and quantify these relationships.

38.1.6 Trend Analysis (T/A):

Trend analysis is a statistical method for determining the equation that best fits the

data in a scatter plot. Trend analysis quantifies the relationships of the data,

determines the equation, and measures the fit of the equation to the data. This

method is also known as curve fitting or least squares.

Trend analysis can determine optimal operating conditions by providing an equation

that describes the relationship between the dependent (output) and independent

(input) variables. An example is the data set concerning experience and scores on the

solder certification test (see Figure 38.14).

Figure 38.14: Scatter Plot Solder Quality and Certification Score

The equation of the regression line, or trend line, provides a clear and understandable

measure of the change caused in the output variable by every incremental change of the

input or independent variable. Using this principle, we can predict the effect of changes

in the process.

288

Project Management MGMT627

One of the most important contributions that can be made by trend analysis is

forecasting. Forecasting enables us to predict what is likely to occur in the future. Based

on the regression line we can forecast what will happen as the independent variable

attain values beyond the existing data.

38.1.7 Process Control Charts (C/C):

The use of control charts focuses on the prevention of defects, rather than their

detection and rejection. In business, government, and industry, economy and

efficiency are always best served by prevention. It costs much more to produce an

unsatisfactory product or service than it does to produce a satisfactory one. There are

many costs associated with producing unsatisfactory goods and services. These costs

are in labor, materials, facilities, and the loss of customers. The cost of producing a

proper product can be reduced significantly by the application of statistical process

control charts.

Control Charts and the Normal Distribution:

The construction, use, and interpretation of control charts is based on the normal

statistical distribution as indicated in Figure 38.15. The centerline of the control

chart represents the average or mean of the data ( ). The upper and lower control

limits (UCL and LCL), respectively, represent this mean plus and minus three

standard deviations of the data either the lowercase s or the Greek letter  (sigma)

represents the standard deviation for control charts.

The normal distribution and its relationship to control charts are represented on the

right of the figure. The normal distribution can be described entirely by its mean

and standard deviation. The normal distribution is a bell-shaped curve (sometimes

called the Gaussian distribution) that is symmetrical about the mean, slopes

downward on both sides to infinity, and theoretically has an infinite range. In the

normal distribution 99.73 percent of all measurements lie within and; this is why

the limits on control charts are called three-sigma limits.

Figure 38.15: The Control Chart and Normal Curve

Companies like Motorola have embarked upon a six-sigma limit rather than a three-

sigma limit. The benefit is shown in Table 38.1 below. With a six-sigma limit, only

two defects per billion are allowed. The cost to maintain a six-sigma limit can be

extremely expensive unless the cost can be spread out over, say, 1 billion units

produced

Control chart analysis determines whether the inherent process variability and the

process average are at stable levels, whether one or both are out of statistical control

289

Project Management MGMT627

(not stable), or whether appropriate action needs to be taken. Another purpose of

using control charts is to distinguish between the inherent, random variability of a

process and the variability attributed to an assignable cause. The sources of random

variability are often referred to as common causes. These are the sources that

cannot be changed readily, without significant restructuring of the process. Special

cause variability, by contrast, is subject to correction within the process under

process control.

Common cause variability or variation: This source of random variation is always

present in any process. It is that part of the variability inherent in the process itself.

The cause of this variation can be corrected only by a management decision to

change the basic process.

Special cause variability or variation: This variation can be controlled at the local

or operational level. Special causes are indicated by a point on the control chart that

is beyond the control limit or by a persistent trend approaching the control limit.

Table 38.1: Attributes of the Normal (Standard) Distribution

To use process control measurement data effectively, it is important to understand

the concept of variation. No two product or process characteristics are exactly alike,

because any process contains many sources of variability. The differences between

products may be large, or they may be almost immeasurably small, but they are

always present. Some sources of variation in the process can cause immediate

differences in the product, such as a change in suppliers or the accuracy of an

individual's work. Other sources of variation, such as tool wear, environmental

changes, or increased administrative control, tend to cause changes in the product

or service only over a longer period of time.

To control and improve a process, we must trace the total variation back to its

sources. Again the sources are common cause and special cause variability.

Common causes are the many sources of variation that always exist within a

process that is in a state of statistical control. Special causes (often called assignable

causes) are any factors causing variation that cannot be adequately explained by any

single distribution of the process output, as would be the case if the process were in

statistical control. Unless all the special causes of variation are identified and

corrected, they will continue to affect the process output in unpredictable ways.

The factors that cause the most variability in the process are the main factors found

on cause-and-effect analysis charts: people, machines, methodology, materials,

measurement, and environment. These causes can either result from special causes

or be common causes inherent in the process.

290

Project Management MGMT627

The theory of control charts suggests that if the source of variation is from chance

alone, the process will remain within the three-sigma limits. When the process goes

out of control, special causes exist. These need to be investigated and corrective

action must be taken.

Control Chart Types:

Just as there are two types of data, continuous and discrete, there are two types of

control charts: variable charts for use with continuous data and attribute charts for

use with discrete data. Each type of control chart can be used with specific types of

data. Table 38.2 provides a brief overview of the types of control charts and their

applications.

Variables charts: Control charts for variables are powerful tools that we can use

when measurements from a process are variable. Examples of variable data are the

diameter of a bearing, electrical output, or the torque on a fastener.

Table 38.2: Types of Control Charts and Application

As shown in Table 38.2, and R charts are used to measure control processes

whose characteristics are continuous variables such as weight, length, ohms, time,

or volume. The p and NP charts are used to measure and control processes

displaying attribute characteristics in a sample. We use p charts when the number of

failures is expressed as a fraction, or NP charts when the failures are expressed as a

number. The c and u charts are used to measure the number or portion of defects in

a single item. The c control chart is applied when the sample size or area is fixed,

and the u chart when the sample size or area is not fixed.

Attribute charts: Although control charts are most often thought of in terms of

variables, there are also versions for attributes. Attribute data have only two values

(conforming/nonconforming, pass/fail, go/no-go, present/absent), but they can still

be counted, recorded, and analyzed. Some examples are: the presence of a required

label, the installation of all required fasteners, the presence of solder drips, or the

continuity of an electrical circuit. We also use attribute charts for characteristics

that are measurable, if the results are recorded in a simple yes/no fashion, such as

the conformance of a shaft diameter when measured on a go/no-go gauge, or the

acceptability of threshold margins to a visual or gauge check.

It is possible to use control charts for operations in which attributes are the basis for

inspection, in a manner similar to that for variables but with certain differences. If

291

Project Management MGMT627

we deal with the fraction rejected out of a sample, the type of control chart used is

called a p chart. If we deal with the actual number rejected, the control chart is

called an NP chart. If articles can have more than one nonconformity, and all are

counted for subgroups of fixed size, the control chart is called a c chart. Finally, if

the number of nonconformities per unit is the quantity of interest, the control chart

is called a u chart.

The power of control charts (Shewhart techniques) lies in their ability to determine

if the cause of variation is a special cause that can be affected at the process level,

or a common cause that requires a change at the management level. The

information from the control chart can then be used to direct the efforts of

engineers, technicians, and managers to achieve preventive or corrective action.

The use of statistical control charts is aimed at studying specific ongoing processes

in order to keep them in satisfactory control. By contrast, downstream inspection

aims to identify defects. In other words, control charts focus on prevention of

defects rather than detection and rejection. It seems reasonable, and it has been

confirmed in practice, that economy and efficiency are better served by prevention

rather than detection.

Control Chart Components:

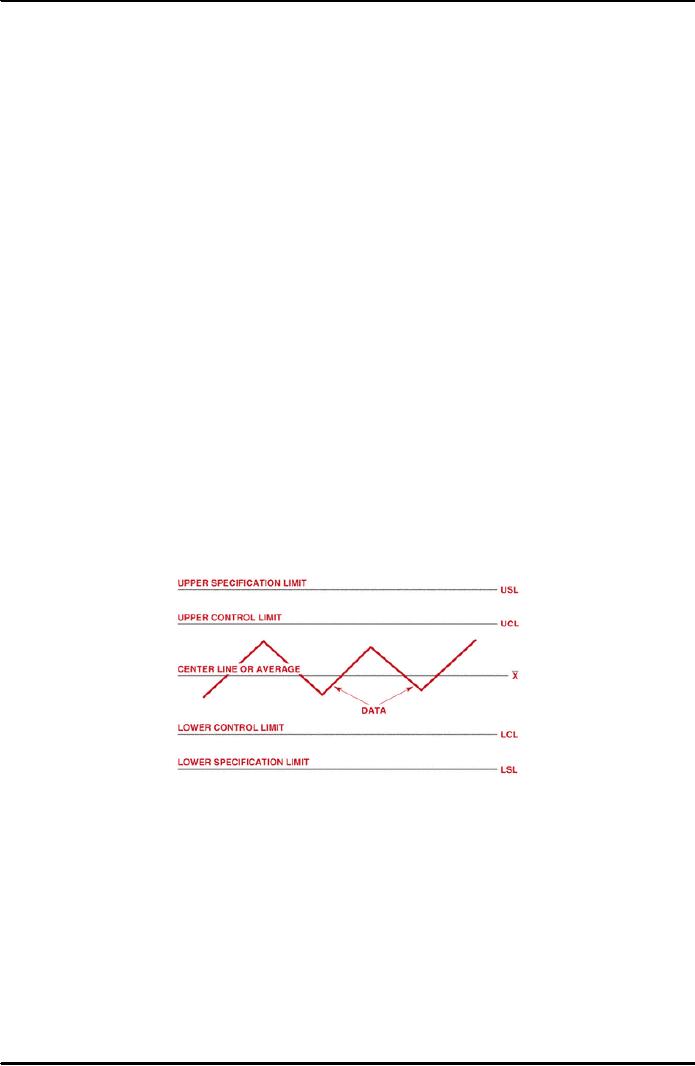
All control charts have certain features in common (Figure 38.16). Each control

chart has a centerline, statistical control limits, and the calculated attribute or

control data. Additionally, some control charts contain specification limits.

The centerline is a solid (unbroken) line that represents the mean or arithmetic

average of the measurements or counts. This line is also referred to as the X bar line

( ). There are two statistical control limits: the upper control limit for values greater

than the mean and the lower control limit for values less than the mean.

Figure 38.16: Control Chart Elements

Specification limits are used when specific parametric requirements exist for a

process, product, or operation. These limits usually apply to the data and are the

pass/fail criteria for the operation. They differ from statistical control limits in that

they are prescribed for a process, rather than resulting from the measurement of the

process.

The data element of control charts varies somewhat among variable and attribute

control charts. We will discuss specific examples as a part of the discussion on

individual control charts.

292

Project Management MGMT627

Control Chart Interpretation:

There are many possibilities for interpreting various kinds of patterns and shifts on

control charts. If properly interpreted, a control chart can tell us much more than

simply whether the process is in or out of control. Experience and training can lead

to much greater skill in extracting clues regarding process behavior, such as that

shown in Figure 38.17. Statistical guidance is invaluable, but an intimate

knowledge of the process being studied is vital in bringing about improvements.

A control chart can tell us when to look for trouble, but it cannot by itself tell us

where to look, or what cause will be found. Actually, in many cases, one of the

greatest benefits from a control chart is that it tells when to leave a process alone.

Sometimes the variability is increased unnecessarily when an operator keeps trying

to make small corrections, rather than letting the natural range of variability

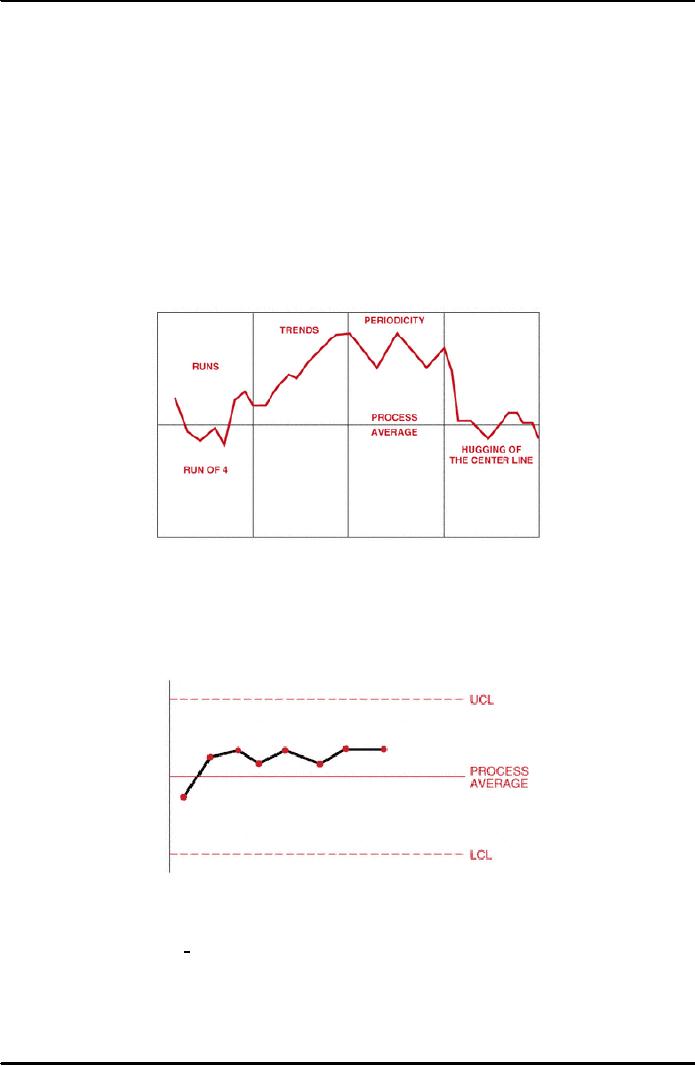
stabilize. The following paragraphs describe some of the ways the underlying

distribution patterns can behave or misbehave.

Figure 38.17: Control Chart Interpretation

Runs: When several successive points line up on one side of the central line, this

pattern is called a run. The number of points in that run is called the length of the

run. As a rule of thumb, if the run has a length of seven points, there is an

abnormality in the process. Figure 38.18 demonstrates an example of a run.

Figure 38.18: Process Run

Trends: If there is a continued rise of all in a series of points, this pattern is called a

trend. In general, if seven consecutive points continue to rise or fall, there is an

abnormality. Often, the points go beyond one of the control limits before reaching

seven. Figure 38.19 demonstrates an example of trends.

293

Project Management MGMT627

Figure 38.19: Control Chart Trends

Periodicity: Points that show the same pattern of change (rise or fall) over

equal intervals denote periodicity. Figure 38.20 demonstrates an example of

periodicity.

Figure 38.20: Control Chart Periodicity

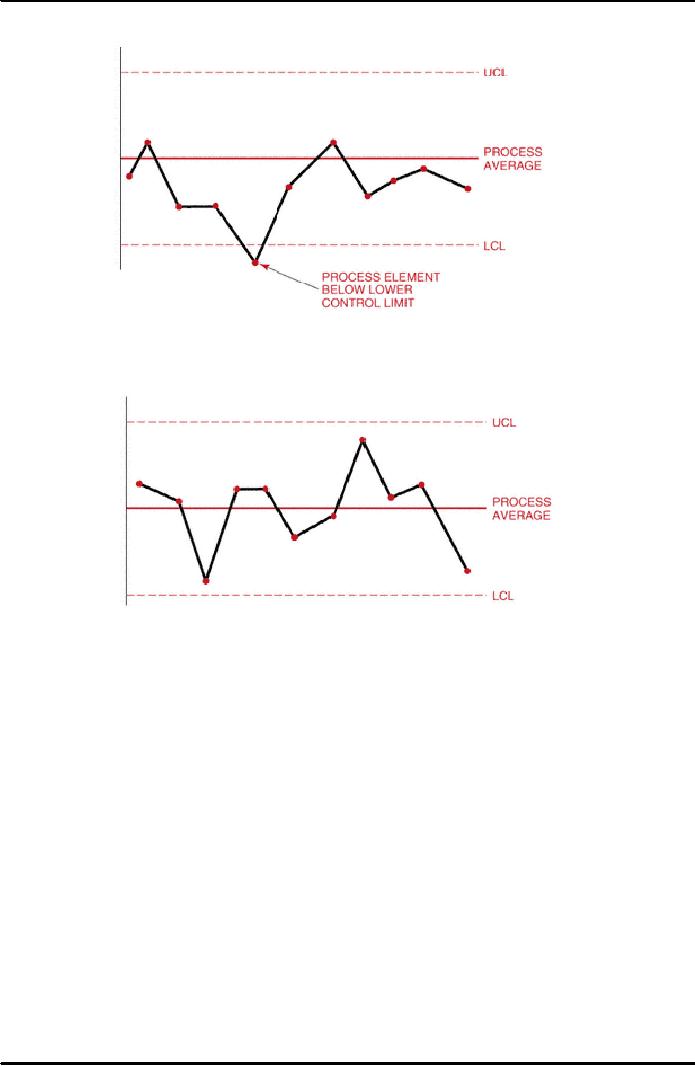
Hugging the centerline or control limit. Points on the control chart that are close to

the central line or to the control limit are said to hug the line. Often, in this

situation, different types of data or data from different factors have been mixed into

the subgroup. In such cases it is necessary to change the sub-grouping, reassemble

the data, and redraw the control chart. To decide whether there is hugging of the

center line, draw two lines on the control chart, one between the centerline and the

UCL and the other between the center line and the LCL. If most of the points are

between these two lines, there is an abnormality. To see whether there is hugging of

one of the control limits; draw line two-thirds of the distance between the center

line and each of the control lines. There is abnormality if 2 out of 3 points, 3 out of

7 points, or 4 out of 10 points lie within the outer one-third zone. The abnormalities

should be evaluated for their cause(s) ad the corrective action taken. Figure 38.21

demonstrates data hugging the LCL.

Figure 38.21: Hugging the Centerline

294

Project Management MGMT627

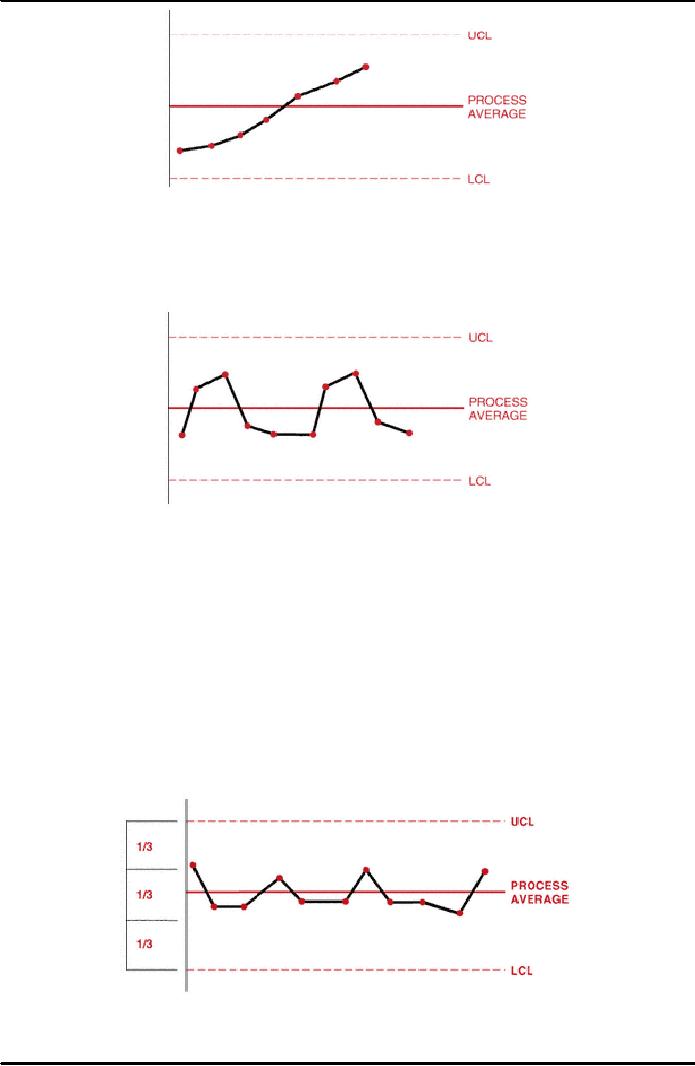
Out of control: An abnormality exists when data points exceed either the

upper or lower control limits. Figure 38.22 illustrates this occurrence.

Figure 38.22: Control Chart Out of Control

In control: No obvious abnormalities appear in the control chart. Figure 38.23

demonstrates this desirable process state.

Figure 38.23: Process in Control

295

Table of Contents: