 |
INVENTORY MANAGEMENT:Economic Production Quantity Assumptions |
| << INVENTORY MANAGEMENT:ABC Classification System, Cycle Counting |
| INVENTORY MANAGEMENT:Independent and Dependent Demand >> |
Production
and Operations Management
MGT613
VU
Lesson
33
INVENTORY
MANAGEMENT
Learning
Objectives
Our
discussion on Inventory Management
would be complete only when we
are able to learn
and
understand
the types of Inventories and objectives of
Inventory Control. This
would ensure that we
are
able
to understand the major reasons for
holding inventories. We would be
able to differentiate between
independent
and dependent demand. We will also
learn the requirements of an effective
inventory
management
system. We will review both
periodic as well as perpetual
Inventory systems. We
will
discuss
in detail the ABC approach with a
suitable example. Our
discussion has focused on
the
objectives
of inventory management, basic EOQ
model, Economic Run Size,
Quantity Discount
Model
with
solved examples.
Example
(In terms of
Percentage)
CNG-LPG
company in Karachi, purchases 5000
compressors a year at Rs.8,000 each.
Ordering costs
are
Rs. 500 and Annual carrying
costs are 20 % of the
purchase price. Compute the Optimal
price and
the
total annual cost of
ordering and carrying the
inventory.
Data
D=Demand
=5,000
S=Ordering=
Rs. 500
H=Holding/Carrying
Cost=0.2 X 8,000=Rs.1600
Example
3 ( In terms of Percentage)
Q0= Sq
Root of ( 2(5,000)(500)/(1600))
=
55.9=56 Compressors
TC=
Carrying costs + Ordering
Costs
=Q0/2 ( H) +
D/Q0 (S)
=
56/2 ( 1600) + 5000/56
(500)
=
28 ( 1600)+ 44,643
=44,800+44,643=Rs.
89,443
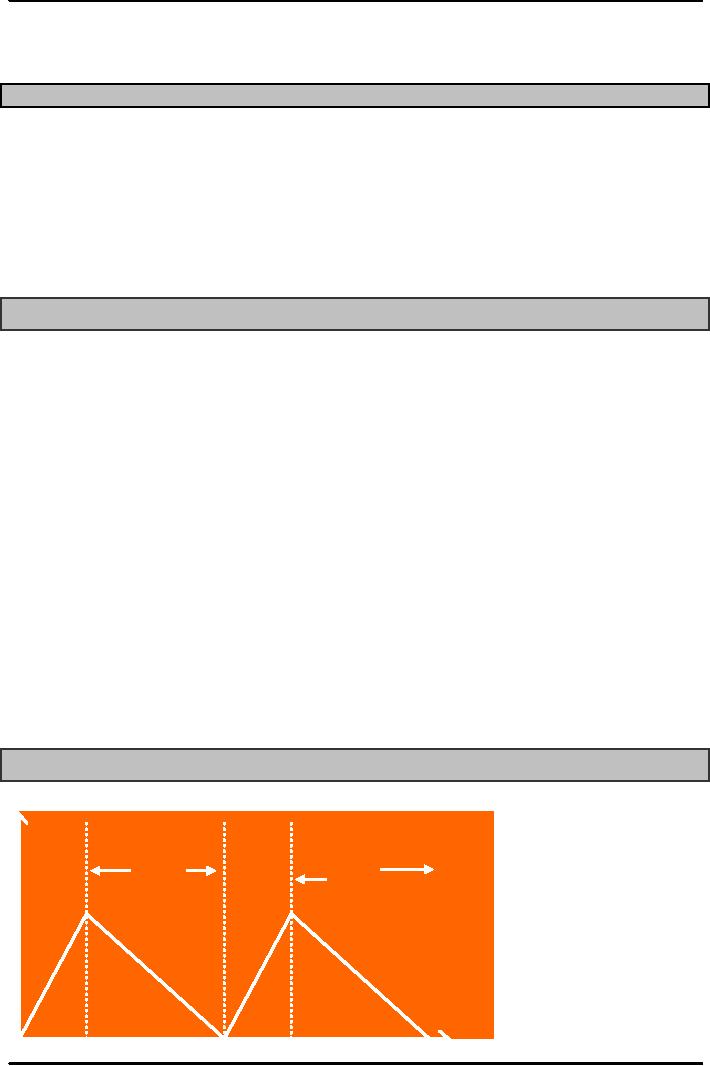
Economic
Production Quantity (EPQ)
Production
Production
Usage
&
Usage Usage
&
Usage
Inventory
Level
152
Production
and Operations Management
MGT613
VU
Economic
Production Quantity (EPQ)
Assumptions
Production
done in batches or lots
Capacity
to produce a part exceeds the part's
usage or demand rate.
Assumptions
of EPQ are similar to EOQ except
orders are received
incrementally during
production.
Economic
Production Quantity
Assumptions
1.
Only
one item is involved
2.
Annual
demand is known
3.
Usage
rate is constant
4.
Usage
occurs continuously
5.
Production
rate is constant
6.
Lead
time does not
vary
7.
No
quantity discounts
Finer
Points of Economic Production Quantity
Model
The
basic EOQ model assumes that
each order is delivered at a
single point in time.
If
the firm is the producer and user,
practical examples indicate that
inventories are
replenished
over
time and not
instantaneously.
If
usage and production ( delivery)
rates are equal, then there
is no buildup of inventory.
Set
up costs in a way our
similar to ordering costs
because they are independent
of lot size.
The
larger the run size, the
fewer the number of runs needed and
hence lower the annual
setup.
The
number of runs is D/Q and the annual
setup cost is equal to the number of
runs per year
times
the cost per run (
D/Q)S.
Total
Cost is
TC
min= Carrying Cost+ Setup
Cost
=
( I max/2)H+ (D/Q0)S
Where
I max= Maximum Inventory
Economic
Run Size
2DS
p
Q0 =
p-u
H
Economic
Production Quantity
Assumptions
Where
p= production rate
U
= usage rate
Economic
Production Quantity
Assumptions
The
Run time ( the production
phase of the cycle) is a function of the
run size and production
rate
Run
time = Q0/p
The
maximum and average
inventory levels are
I
max = Q0/p
(p-u)
I
average= I max/2
153

Production
and Operations Management
MGT613
VU
Example
(Economic Run Size)
Example
for Economic Run
Size
A
firm in Sialkot produces
250,000 each world class
footballs for both domestic and
international
markets
. It can make footballs at a rate of
2000 per day. The footballs
are manufactured uniformly
over
the whole year. Carrying
cost is Rs. 100 per football
and Setup cost for a
production run is Rs.
2500.
The manufacturing unit
operates for 250 days per
year.
Determine
the
1.
Optimal Run Size.
2.
Minimum total annual cost
for carrying and setup
cost.
3.
Cycle time for the Optimal
Run Size.
4.
Run time by using the
formula
2DS
p
Q0 =
p-u
H
Solution
1.
Optimal Run Size.
=
Sq Root (2 X 250,000 X 2500/100 )( Sq
Root (2 000 /2000-1000
))
=
2500( sq.root2X2)=5000
footballs.
2.
Minimum total annual cost
for carrying and setup
cost.
=
Carrying Cost + Set up
Cost
=(
I max/2)H+ ( D/Q0)S
Where
I max= Q0/p
((p-u))=5000/2000(1000)
=2500
footballs
Now
TC= 2500/2 X 100 +
(250,000/5000 )(2500)
=1250
X 100 + 125,000
=125,000+
125,000
=
Rs. 250,000.
3.
Cycle time for the Optimal
Run Size.
Q0/U=5000/1000=
5 days
4.
Run time
Q0/p=5000/2000=
2.5 days
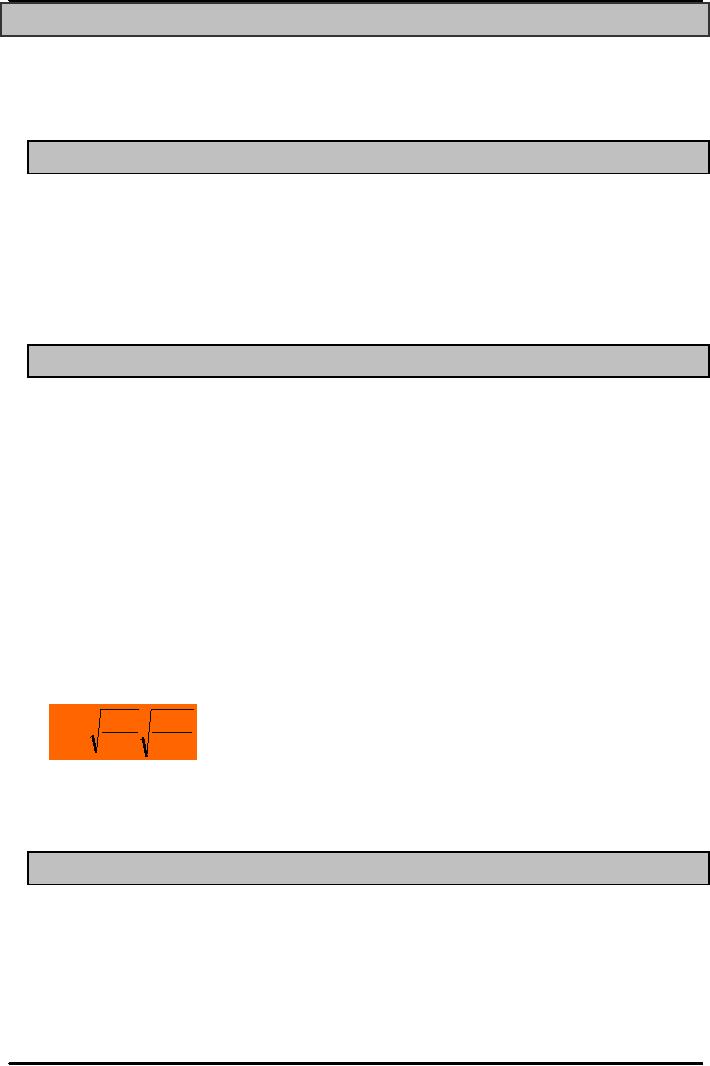
Quantity
Discount : Price reductions for large
orders are called Quantity
Discounts.
Total
Costs with Purchasing
Cost
Annual
Annual
Purchasing
+
carrying
ordering
+
TC
=
cost
cost
cost
Q
DS
PD
H
TC
=
+
+
Q
2
Total
Costs with PD
154
Production
and Operations Management
MGT613
VU
C
O
S
Adding
Purchasing cost
TC
with PD
T
doesn't
change EOQ
TC
without PD
PD
0
Quantity
EOQ
Example
for Optimal Order Quantity
and Total Cost
The
maintenance department of a large cardiology
hospital in Islamabad uses about
1200 cases of
corrosion
removal liquid, used for
maintenance of hospital. Ordering costs
are Rs 100, carrying
cost
are
Rs 20 per case, and the new
price schedule indicates that
orders of less than 50 cases
will cost
Rs
1250 per case, 50 to 79 cases
will cost Rs 1150 per case ,
80 to 99 cases will cost Rs
1050 per
case
and larger costs will be Rs
1000 per case.
Determine
the Optimal Order Quantity and the
Total Cost.
Given
Data
D=1200
case.
S=
Rs. 100 per case
H=Rs.20
per case
Range
Price
1
to 49
Rs
1250
50
to 79
Rs
1150
80
to 99
Rs
1050
100
or more
Rs
1000
Compute
the Common EOQ=Sq Root (2DS/H)
=
Sq Root (2 X 100 X
1200/20)
=Sq
Root (12000)
=109.5=110
cases which would be brought
at 1000 per order
The
total Cost to Purchase 1200
cases per year would
be
TC=
Carrying Cost+ Order Cost+
Purchase Cost
=(Q/2)H+(D/Q0)S+PD
=(110/2)20+(1200/110)100+1200X
1000
=1100+1091+12000,000
=Rs.
1,202,191
155

Production
and Operations Management
MGT613
VU
When
to Reorder with EOQ Ordering
Reorder
Point - When the quantity on hand of an
item drops to this amount, the item is
reordered.
Safety
Stock - Stock that is held
in excess of expected demand due to
variable demand rate
and/or
lead
time.
Service
Level - Probability that
demand will not exceed
supply during lead
time.
Example
for Reorder Point
An
apartment complex in Quetta requires water
for its home
use.
Usage=
2 barrels a day
Lead
time= 5 days
ROP=
Usage X Lead Time
=
2 barrels a day X 7 = 14 barrels
Determinants
of the Reorder Point
1.
The
rate of demand
2.
The
lead time
3.
Stock
out risk (safety
stock)
4.
Demand
and/or lead time
variability
Example
An
owner of a Montessori equipment
firm in Karachi, determined
from historical records
that
demand
for wood required for
Montessori equipment averages 25
tones per anum. His operations
management
expertise allowed him to determine the
demand during lead that
could be described by
a
normal distribution that has
a mean of 25 tons and a standard
deviation of 2.5 tons, with a
stock
out
risk not limited to 6
percent.
a.
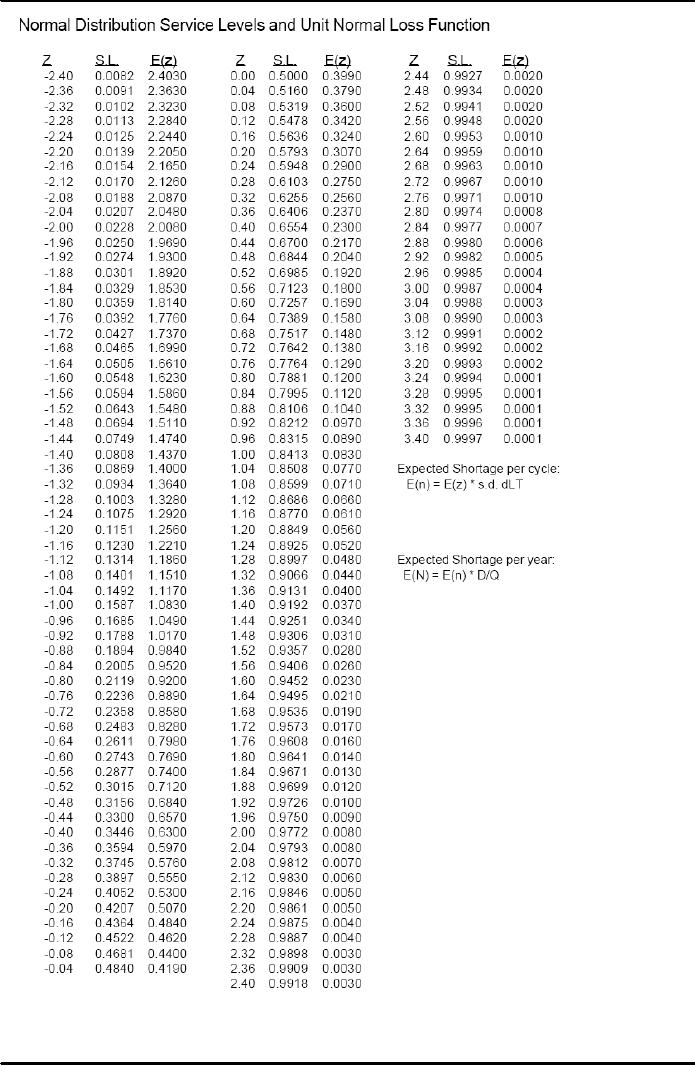
Appropriate value of Z? Please
use the table given on the
next page (9)
b.
Safety stock level?
c.
Reorder Point?
d.
Expected weight of wood short for
any order cycle, if he wants
to maintain a service level of
80%
Use the attached service level
table. Please use the
table given on page (
10)
e.
Annual Service Level, if service level
=80
156
Production
and Operations Management
MGT613
VU
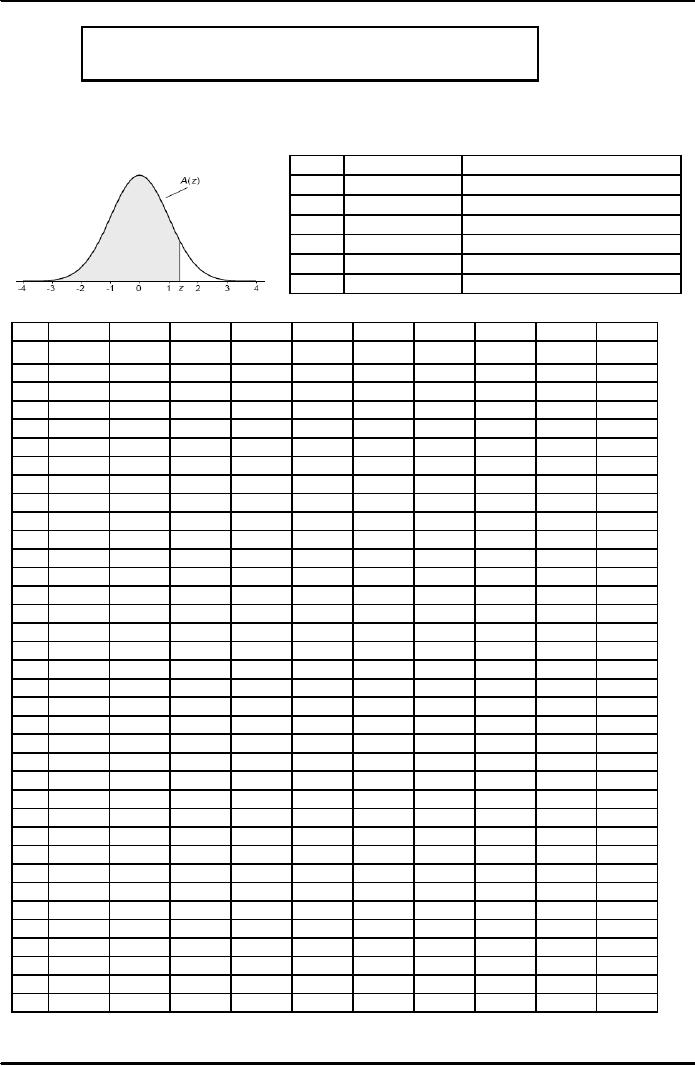
Area
under the standardizes normal curve
from -∞
to
z
A(z)
is the integral of the standardized normal
distribution from ∞-to z
(in other words, the area
under the curve
to
the left of z). It gives the probability
of a normal random variable not
being more than z standard
deviations
above
its mean. Values of z of
particular importance:
z
A(z)
1.645
0.9500
Lower
limit of right 5%
tail
1.960
0.9750
Lower
limit of right 2.5%
tail
2.326
0.9900
Lower
limit of right 1%
tail
2.576
0.9950
Lower
limit of right 0.5%
tail
3.090
0.9990
Lower
limit of right 0.1%
tail
3.291
0.9995
Lower
limit of right 0.05%
tail
Cumulative
Standardized Normal
Distribution
z
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.0
0.5000
0.5040
0.5080
0.5120
0.5160
0.5199
0.5239
0.5279
0.5319
0.5359
0.1
0.5398
0.5438
0.5478
0.5517
0.5557
0.5596
0.5636
0.5675
0.5714
0.5753
0.2
0.5793
0.5832
0.5871
0.5910
0.5948
0.5987
0.6026
0.6064
0.6103
0.6141
0.3
0.6179
0.6217
0.6255
0.6293
0.6331
0.6368
0.6406
0.6443
0.6480
0.6517
0.4
0.6554
0.6591
0.6628
0.6664
0.6700
0.6736
0.6772
0.6808
0.6844
0.6879
0.5
0.6915
0.6950
0.6985
0.7019
0.7054
0.7088
0.7123
0.7157
0.7190
0.7224
0.6
0.7257
0.7291
0.7324
0.7357
0.7389
0.7422
0.7454
0.7486
0.7517
0.7549
0.7
0.7580
0.7611
0.7642
0.7673
0.7704
0.7734
0.7764
0.7794
0.7823
0.7852
0.8
0.7881
0.7910
0.7939
0.7967
0.7995
0.8023
0.8051
0.8078
0.8106
0.8133
0.9
0.8159
0.8186
0.8212
0.8238
0.8264
0.8289
0.8315
0.8340
0.8365
0.8389
1.0
0.8413
0.8438
0.8461
0.8485
0.8508
0.8531
0.8554
0.8577
0.8599
0.8621
1.1
0.8643
0.8665
0.8686
0.8708
0.8729
0.8749
0.8770
0.8790
0.8810
0.8830
1.2
0.8849
0.8869
0.8888
0.8907
0.8925
0.8944
0.8962
0.8980
0.8997
0.9015
1.3
0.9032
0.9049
0.9066
0.9082
0.9099
0.9115
0.9131
0.9147
0.9162
0.9177
1.4
0.9192
0.9207
0.9222
0.9236
0.9251
0.9265
0.9279
0.9292
0.9306
0.9319
1.5
0.9332
0.9345
0.9357
0.9370
0.9382
0.9394
0.9406
0.9418
0.9429
0.9441
1.6
0.9452
0.9463
0.9474
0.9484
0.9495
0.9505
0.9515
0.9525
0.9535
0.9545
1.7
0.9554
0.9564
0.9573
0.9582
0.9591
0.9599
0.9608
0.9616
0.9625
0.9633
1.8
0.9641
0.9649
0.9656
0.9664
0.9671
0.9678
0.9686
0.9693
0.9699
0.9706
1.9
0.9713
0.9719
0.9726
0.9732
0.9738
0.9744
0.9750
0.9756
0.9761
0.9767
2.0
0.9772
0.9778
0.9783
0.9788
0.9793
0.9798
0.9803
0.9808
0.9812
0.9817
2.1
0.9821
0.9826
0.9830
0.9834
0.9838
0.9842
0.9846
0.9850
0.9854
0.9857
2.2
0.9861
0.9864
0.9868
0.9871
0.9875
0.9878
0.9881
0.9884
0.9887
0.9890
2.3
0.9893
0.9896
0.9898
0.9901
0.9904
0.9906
0.9909
0.9911
0.9913
0.9916
2.4
0.9918
0.9920
0.9922
0.9925
0.9927
0.9929
0.9931
0.9932
0.9934
0.9936
2.5
0.9938
0.9940
0.9941
0.9943
0.9945
0.9946
0.9948
0.9949
0.9951
0.9952
2.6
0.9953
0.9955
0.9956
0.9957
0.9959
0.9960
0.9961
0.9962
0.9963
0.9964
2.7
0.9965
0.9966
0.9967
0.9968
0.9969
0.9970
0.9971
0.9972
0.9973
0.9974
2.8
0.9974
0.9975
0.9976
0.9977
0.9977
0.9978
0.9979
0.9979
0.9980
0.9981
2.9
0.9981
0.9982
0.9982
0.9983
0.9984
0.9984
0.9985
0.9985
0.9986
0.9986
3.0
0.9987
0.9987
0.9987
0.9988
0.9988
0.9989
0.9989
0.9989
0.9990
0.9990
3.1
0.9990
0.9991
0.9991
0.9991
0.9992
0.9992
0.9992
0.9992
0.9993
0.9993
3.2
0.9993
0.9993
0.9994
0.9994
0.9994
0.9994
0.9994
0.9995
0.9995
0.9995
3.3
0.9995
0.9995
0.9995
0.9996
0.9996
0.9996
0.9996
0.9996
0.9996
0.9997
3.4
0.9997
0.9997
0.9997
0.9997
0.9997
0.9997
0.9997
0.9997
0.9997
0.9998
3.5
0.9998
0.9998
0.9998
0.9998
0.9998
0.9998
0.9998
0.9998
0.9998
0.9998
157
Production
and Operations Management
MGT613
VU
.
158
Production
and Operations Management
MGT613
VU
SOLUTION
a.
Expected Lead Time Demand= 25 tonnes,
also σdLT= 2.5 tonnes,
Risk= 6%. Using the
given
table
values, 1-0.06=.9400 therefore +
Z=1.1.55
b.
The safety stock = ZσdLT= 1.55 x 2.50
tonnes= 3.875 tonnes
c.
Reorder Point =
Expected
Lead Time Demand + Safety
Stock
=
25
tonnes + 3.875=28.875
tonnes
d.
From the Service Level Table,
Lead time Service Level z=0.8
therefore E(z)=0.7881,using the
formula
E(n)=E(z) X σdLT
Now
Since σ
dLT= 2.5
tonnes
Therefore
E(n)=0.7881(2.50)=39.41 tonnes= 1.97025
tonnes
e.
SL annual= 1-E(z) σdLT/Q
Now
Since Q= 25 tonnes, E(z)=
We
can calculate the Annual Service Level by
substituting values in the formula
above
SL
annual=
1-0.7881(50)/1000=1-39.405/1000=1-0.03941=0.961
Fixed-Order-Interval
Model
1.
Orders
are placed at fixed time
intervals.
2.
Order
quantity for next
interval?
3.
Suppliers
might encourage fixed
intervals.
4.
May
require only periodic checks
of inventory levels.
5.
Risk
of stock out.
Summary
In
this lecture we studied
various important concepts
relating to Inventory Management.
Most
importantly
we learnt how to make use of
statistical tables to calculate lead
points and service
levels.
This
lecture forms the basis for
Supply Chain Management and
Just In Time Production
Systems.
159
Table of Contents:
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:Decision Making
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:Strategy
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:Service Delivery System
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:Productivity
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:The Decision Process
- INTRODUCTION TO PRODUCTION AND OPERATIONS MANAGEMENT:Demand Management
- Roadmap to the Lecture:Fundamental Types of Forecasts, Finer Classification of Forecasts
- Time Series Forecasts:Techniques for Averaging, Simple Moving Average Solution
- The formula for the moving average is:Exponential Smoothing Model, Common Nonlinear Trends
- The formula for the moving average is:Major factors in design strategy
- The formula for the moving average is:Standardization, Mass Customization
- The formula for the moving average is:DESIGN STRATEGIES
- The formula for the moving average is:Measuring Reliability, AVAILABILITY
- The formula for the moving average is:Learning Objectives, Capacity Planning
- The formula for the moving average is:Efficiency and Utilization, Evaluating Alternatives
- The formula for the moving average is:Evaluating Alternatives, Financial Analysis
- PROCESS SELECTION:Types of Operation, Intermittent Processing
- PROCESS SELECTION:Basic Layout Types, Advantages of Product Layout
- PROCESS SELECTION:Cellular Layouts, Facilities Layouts, Importance of Layout Decisions
- DESIGN OF WORK SYSTEMS:Job Design, Specialization, Methods Analysis
- LOCATION PLANNING AND ANALYSIS:MANAGING GLOBAL OPERATIONS, Regional Factors
- MANAGEMENT OF QUALITY:Dimensions of Quality, Examples of Service Quality
- SERVICE QUALITY:Moments of Truth, Perceived Service Quality, Service Gap Analysis
- TOTAL QUALITY MANAGEMENT:Determinants of Quality, Responsibility for Quality
- TQM QUALITY:Six Sigma Team, PROCESS IMPROVEMENT
- QUALITY CONTROL & QUALITY ASSURANCE:INSPECTION, Control Chart
- ACCEPTANCE SAMPLING:CHOOSING A PLAN, CONSUMER’S AND PRODUCER’S RISK
- AGGREGATE PLANNING:Demand and Capacity Options
- AGGREGATE PLANNING:Aggregate Planning Relationships, Master Scheduling
- INVENTORY MANAGEMENT:Objective of Inventory Control, Inventory Counting Systems
- INVENTORY MANAGEMENT:ABC Classification System, Cycle Counting
- INVENTORY MANAGEMENT:Economic Production Quantity Assumptions
- INVENTORY MANAGEMENT:Independent and Dependent Demand
- INVENTORY MANAGEMENT:Capacity Planning, Manufacturing Resource Planning
- JUST IN TIME PRODUCTION SYSTEMS:Organizational and Operational Strategies
- JUST IN TIME PRODUCTION SYSTEMS:Operational Benefits, Kanban Formula
- JUST IN TIME PRODUCTION SYSTEMS:Secondary Goals, Tiered Supplier Network
- SUPPLY CHAIN MANAGEMENT:Logistics, Distribution Requirements Planning
- SUPPLY CHAIN MANAGEMENT:Supply Chain Benefits and Drawbacks
- SCHEDULING:High-Volume Systems, Load Chart, Hungarian Method
- SEQUENCING:Assumptions to Priority Rules, Scheduling Service Operations
- PROJECT MANAGEMENT:Project Life Cycle, Work Breakdown Structure
- PROJECT MANAGEMENT:Computing Algorithm, Project Crashing, Risk Management
- Waiting Lines:Queuing Analysis, System Characteristics, Priority Model