TIME VALUE OF MONEY:Future Value, Present Value

<< FINANCIAL INSTITUTIONS:The structure of the financial industry

APPLICATION OF PRESENT VALUE CONCEPTS:Compound Annual Rates >>

Money & Banking MGT411

Lesson 8

TIME VALUE OF MONEY

Time Value of Money

Future Value Concepts

Present value

Application in financial environment

Time Value of Money

Credit is one of the critical mechanisms we have for allocating resources.

Even the simplest financial transaction, like saving some of your paycheck each month to buy a

car, would be impossible.

Corporations, most of which survive from day to day by borrowing to finance their activities,

would not be able to function.

Yet even so, most people still take a dim view of the fact that lenders charge interest.

The main reason for the enduring unpopularity of interest comes from the failure to appreciate

the fact that lending has an opportunity cost.

Think of it from the point of view of the lender.

Extending a loan means giving up the alternatives. While lenders can eventually recoup the sum

they lend, neither the time that the loan was outstanding nor the opportunities missed during that

time can be gotten back.

So interest isn't really "the breeding of money from money,'' as Aristotle put it; it's more like a

rental fee that borrowers must pay lenders to compensate them for lost opportunities.

It's no surprise that in today's world, interest rates are of enormous importance to virtually

everyone

Individuals, businesses, and governments

They link the present to the future, allowing us to compare payments made on different dates.

Interest rates also tell us the future reward for lending today, as well as the cost of borrowing

now and repaying later.

To make sound financial decisions, we must learn how to calculate and compare different rates

on various financial instruments

Future Value

Future Value is the value on some future date of an investment made today.

To calculate future value we multiply the present value by the interest rate and add that amount

of interest to the present value.

Interest

PV*i

$100 + $100(0.05)

= $105

PV = Present Value

FV = Future Value

i = interest rate (as a percentage)

The higher the interest rate (or the amount invested) the higher the future value.

Future Value in one year

FV = PV*(1+i)

Money & Banking MGT411

Now we need to figure out what happens when the time to repayment varies

When we consider investments with interest payments made for more than one year we need to

consider compound interest, or the fact that interest will be paid on interest

Future Value in two years

$100+$100(0.05) +$100(0.05) + $5(0.05) =$110.25

Present Value of the Initial Investment + Interest on the initial investment in the 1st Year + Interest on

the initial investment in the 2nd Year+ Interest on the Interest from the 1stYear in the 2nd Year

= Future Value in Two Years

General Formula for compound interest Future value of an investment of PV in n years at interest rate

i (measured as a decimal, or 5% = .05)

FVn = PV*(1+i) n

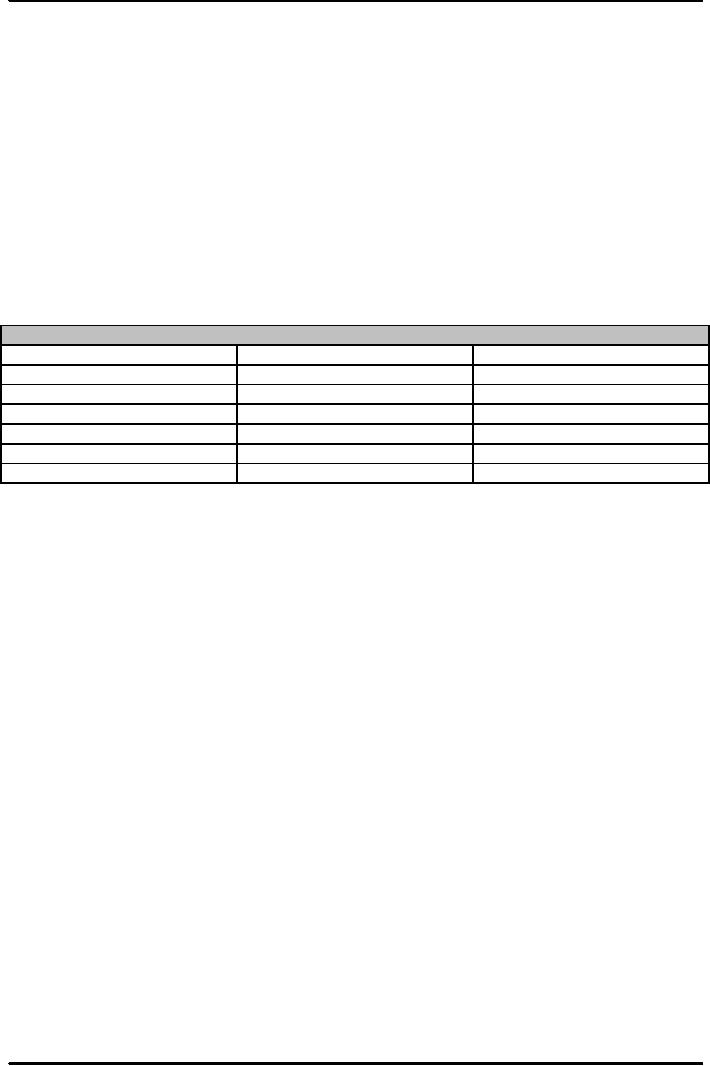
Table: Computing the Future Value of $100 at 5% annual interest rate

Years into future

Computation

Future value

$100(0.5)

$105.00

$100(0.5)

$110.25

$100(0.5)

$115.76

$100(0.5)

$121.55

$100(0.5)

$127.63

$100(0.5)

$162.89

Note:

Both n and i must be measured in same time units--if i is annual, then n must be in years, so future

value of $100 in 18 months at 5% is

FV = 100 *(1+.05)1.5

How useful it is?

If you put $1,000 per year into bank at 4% interest, how much would you have saved after 40

years?

Taking help of future value concept, the accumulated amount through the saving will be

$98,826 more than twice the $40,000 you invested

How does it work?

The first $1,000 is deposited for 40 years so its future value is

$1,000 x (1.04)40 = 4,801.02

The 2nd $1,000 is deposited for 39 years so its future value is

$1,000 x (1.04)39 = 4,616.37

And so on.....up to the $1,000 deposited in the 40th year

Adding up all the future values gives you the amount of $98,826

Present Value

Present Value (PV) is the value today (in the present) of a payment that is promised to be made

in the future. OR

Present Value is the amount that must be invested today in order to realize a specific amount on

a given future date.

To calculate present value we invert the future value calculation;

We divide future value by one plus the interest rate (to find the present value of a payment to be

made one year from now).

Solving the Future Value Equation

Money & Banking MGT411

FV = PV*(1+i)

Present Value of an amount received in one year.

Example:

$100 received in one year, i=5%

PV=$100/ (1+.05) = $95.24

Note:

FV = PV*(1+i) = $95.24*(1.05) = $100

For payments to be made more than one year from now we divide future value by one plus the

interest rate raised to the nth power where n is the number of years

Present Value of $100 received n years in the future:

Example

Present Value of $100 received in 2 ½ years and an interest rate of 8%.

PV = $100 / (1.08)2.5 = $82.50

Note:

FV =$82.50 * (1.08)2.5 = $100

Table of Contents: