MEASURING RISK:Variance, Standard Deviation, Value at Risk, Risk Aversion

<< BOND PRICING & RISK:Valuing the Principal Payment, Risk

EVALUATING RISK:Deciding if a risk is worth taking, Sources of Risk >>

Money & Banking MGT411

Lesson 11

MEASURING RISK

Measuring Risk

Variance and Standard Deviation

Value at Risk (VAR)

Risk Aversion & Risk Premium

Measuring Risk

Most of us have an intuitive sense for risk and its measurement;

The wider the range of outcomes the greater the risk

A financial instrument with no risk at all is a risk-free investment or a risk-free asset;

Its future value is known with certainty and

Its return is the risk-free rate of return

If the risk-free return is 5 percent, a $1000 risk-free investment will pay $1050, its expected

value, with certainty.

If there is a chance that the payoff will be either more or less than $1050, the investment is

risky.

We can measure risk by measuring the spread among an investment's possible outcomes. There

are two measures that can be used:

Variance and Standard Deviation

Measure of spread

Value at Risk (VAR)

Measure of riskiness of worst case

Variance

The variance is defined as the probability weighted average of the squared deviations of the

possible outcomes from their expected value

To calculate the variance of an investment, following steps are involved:

Compute expected value

Subtract expected value from each possible payoff

Square each result

Multiply by its probability

Add up the results

Compute the expected value:

($1400 x ½) + ($700 x ½) = $1050.

Subtract this from each of the possible payoffs:

$1400-$1050= $350

$700-$1050= $350

Square each of the results:

$3502 = 122,500(dollars)2 and

($350)2 = 122,500(dollars)2

Multiply each result times its probability and adds up the results:

½ [122,500(dollars)2] + ½ [122,500(dollars)2]

= 122,500(dollars)2

Money & Banking MGT411

More compactly;

Variance = ½($1400-$1050)2 + ½($700-$1050)2

= 122,500(dollars)2

Standard Deviation

The standard deviation is the square root of the variance, or:

Standard Deviation (case 1) =$350

Standard Deviation (case 2) =$528

The greater the standard deviation, the higher the risk

It more useful because it is measured in the same units as the payoffs (that is, dollars and not

squared dollars)

The standard deviation can then also be converted into a percentage of the initial investment,

providing a baseline against which we can measure the risk of alternative investments

Given a choice between two investments with the same expected payoff, most people would

choose the one with the lower standard deviation because it would have less risk

Value at Risk

Sometimes we are less concerned with the spread of possible outcomes than we are with the

value of the worst outcome.

To assess this sort of risk we use a concept called "value at risk."

Value at risk measures risk at the maximum potential loss

Risk Aversion

Most people don't like risk and will pay to avoid it; most of us are risk averse

A risk-averse investor will always prefer an investment with a certain return to one with the

same expected return, but any amount of uncertainty.

Buying insurance is paying someone to take our risks, so if someone wants us to take on risk we

must be paid to do so

Risk Premium

The riskier an investment the higher the compensation that investors require for holding it

the higher the risk premium

Riskier investments must have higher expected returns

There is a trade-off between risk and expected return;

You can't get a high return without taking considerable risk.

Money & Banking MGT411

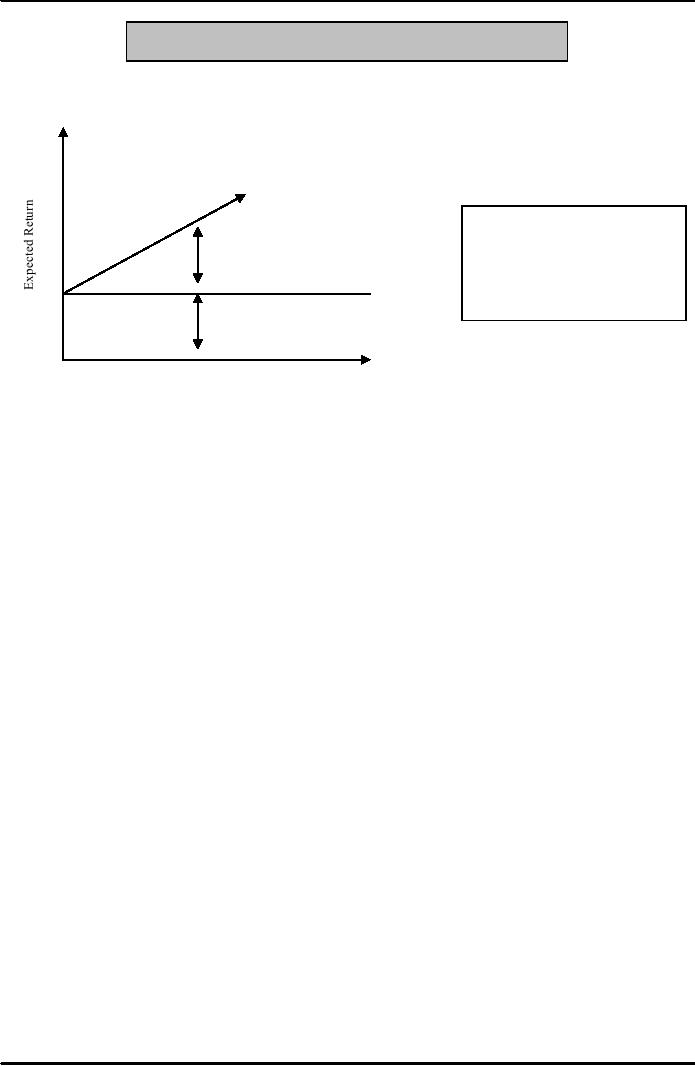
Figure: The Trade-off between Risk and Expected Return

Higher Risk=Higher Expected Return

The higher the risk, the higher

the expected return. The risk

Risk Premium

premium equals the expected

return on the risky investment

minus the risk-free return.

Risk- Free Return

Risk

Table of Contents: