BOND PRICING & RISK:Valuing the Principal Payment, Risk

<< APPLICATION OF PRESENT VALUE CONCEPTS:Compound Annual Rates

MEASURING RISK:Variance, Standard Deviation, Value at Risk, Risk Aversion >>

Money & Banking MGT411

Lesson 10

BOND PRICING & RISK

Bond Pricing

Real Vs Nominal Interest Rates

Risk

Characteristics

Measurement

Bond Pricing

A bond is a promise to make a series of payments on specific future date.

It is a legal contract issued as part of an arrangement to borrow

The most common type is a coupon bond, which makes annual payments called coupon

payments

The percentage rate is called the coupon rate

The bond also specifies a maturity date (n) and has a final payment (F), which is the principal,

face value, or par value of the bond

The price of a bond is the present value of its payments

To value a bond we need to value the repayment of principal and the payments of interest

Valuing the Principal Payment

A straightforward application of present value where n represents the maturity of the bond

Valuing the Coupon Payments:

Requires calculating the present value of the payments and then adding them; remember,

present value is additive

Valuing the Coupon Payments plus Principal

Means combining the above

Payment stops at the maturity date. (n)

A payment is for the face value (F) or principle of the bond

Coupon Bonds make annual payments called, Coupon Payments (C), based upon an interest

rate, the coupon rate (ic), C=ic*F

A bond that has a $100 principle payment in n years. The present

Value (PBP) of this is now:

$ 100

(1 + i )

If the bond has n coupon payments (C), where C= ic * F, the Present Value (PCP) of the coupon

payments is:

P CP =

+ ...... +

(1 + i ) 1

(1 + i ) 2

(1 + i ) 3

(1 + i ) n

Money & Banking MGT411

Present Value of Coupon Bond (PCB) = Present value of Yearly Coupon Payments (PCP) + Present Value

of the Principal Payment (PBP)

C ⎤

⎡ C

PCB = PCP + PBP = ⎢

+ ...... +

⎥

(1 + i) n ⎦ (1 + i) n

⎣ (1 + i) (1 + i)

(1 + i) 3

Note:

The value of the coupon bond rises when the yearly coupon payments rise and when the interest

rate falls

Lower interest rates mean higher bond prices and vice versa.

The value of a bond varies inversely with the interest rate used to discount the promised

payments

Real and Nominal Interest Rates

So far we have been computing the present value using nominal interest rates (i), or interest

rates expressed in current-dollar terms

But inflation affects the purchasing power of a dollar, so we need to consider the real interest

rate (r), which is the inflation-adjusted interest rate.

The Fisher equation tells us that the nominal interest rate is equal to the real interest rate plus

the expected rate of inflation

Fisher Equation:

i=r+ e

r = i - še

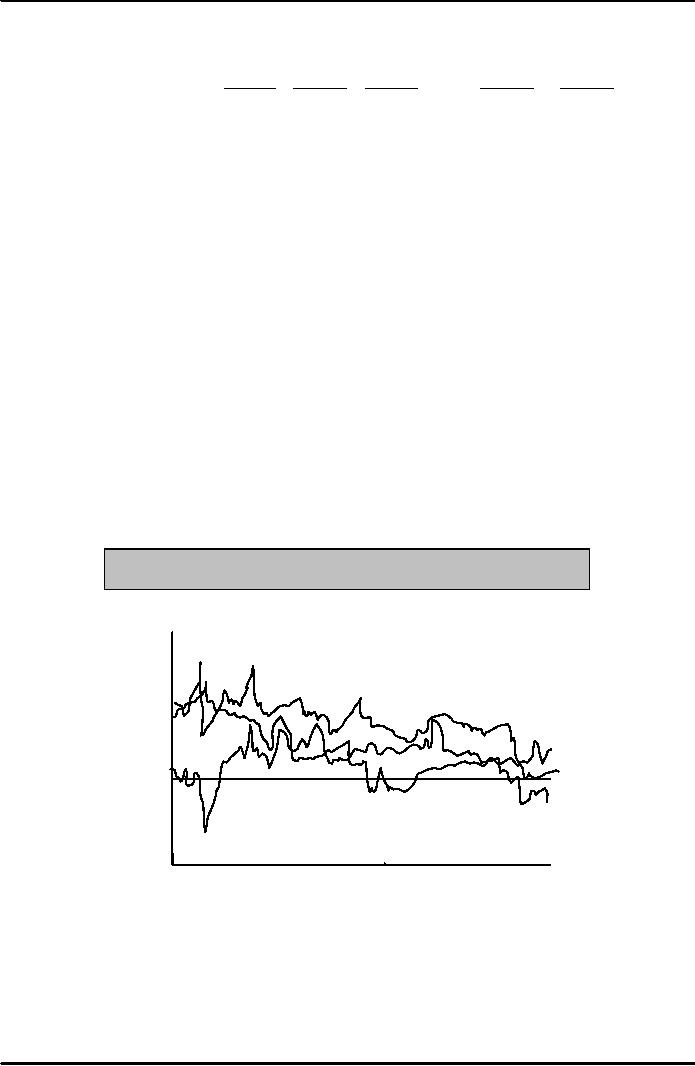
Figure: Nominal Interest rates, Inflation, and real interest rates

-5

-10

1982

1985

1988

1991

1994 1997 2000

1979

2003

Money & Banking MGT411

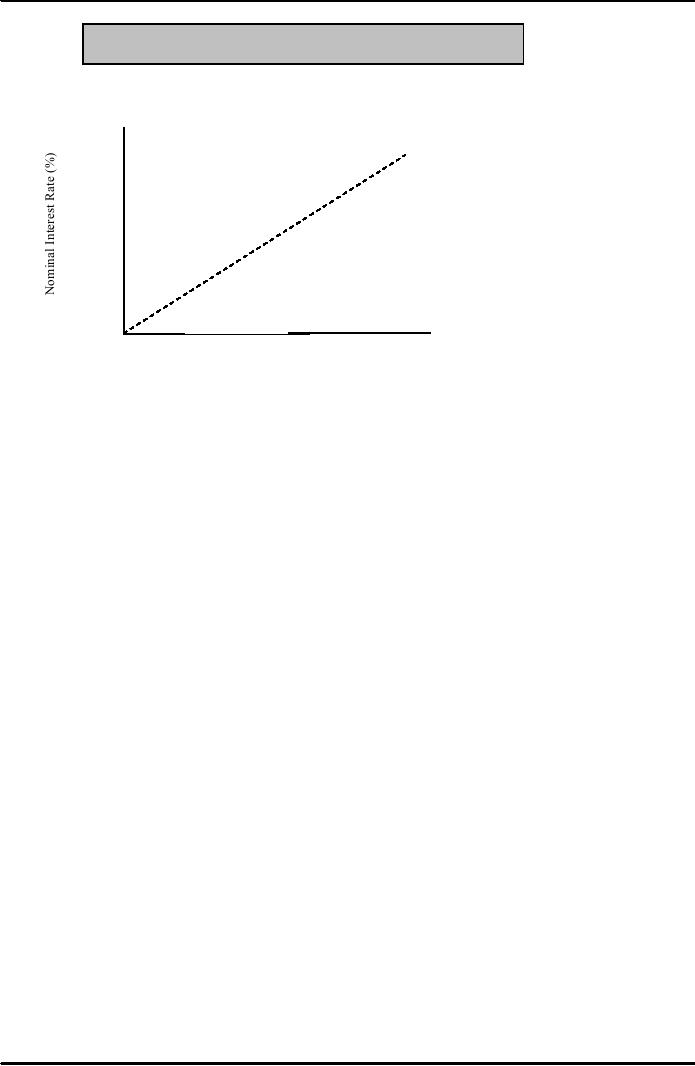
Figure: Inflation and Nominal Interest Rates, April 2004

Turkey

45º line

Brazil

Russia

South Africa

Inflation (%)

Risk

Every day we make decisions that involve financial and economic risk.

How much car insurance should we buy?

Should we refinance the home loan now or a year from now?

Should we save more for retirement, or spend the extra money on a new car?

Interestingly enough, the tools we use today to measure and analyze risk were first developed to

help players analyze games of chance.

For thousands of years, people have played games based on a throw of the dice, but they had

little understanding of how those games actually worked

Since the invention of probability theory, we have come to realize that many everyday events,

including those in economics, finance, and even weather forecasting, are best thought of as

analogous to the flip of a coin or the throw of a die

Still, while experts can make educated guesses about the future path of interest rates, inflation,

or the stock market, their predictions are really only that--guess.

And while meteorologists are fairly good at forecasting the weather a day or two ahead,

economists, financial advisors, and business gurus have dismal records.

So understanding the possibility of various occurrences should allow everyone to make better

choices. While risk cannot be eliminated, it can often be managed effectively.

Finally, while most people view risk as a curse to be avoided whenever possible, risk also

creates opportunities.

The payoff from a winning bet on one hand of cards can often erase the losses on a losing hand.

Thus the importance of probability theory to the development of modern financial markets is

hard to overemphasize.

People require compensation for taking risks. Without the capacity to measure risk, we could

not calculate a fair price for transferring risk from one person to another, nor could we price

stocks and bonds, much less sell insurance.

The market for options didn't exist until economists learned how to compute the price of an

option using probability theory

We need a definition of risk that focuses on the fact that the outcomes of financial and

economic decisions are almost always unknown at the time the decisions are made.

Risk is a measure of uncertainty about the future payoff of an investment, measured over some

time horizon and relative to a benchmark.

Money & Banking MGT411

Characteristics of risk

Risk can be quantified.

Risk arises from uncertainty about the future.

Risk has to do with the future payoff to an investment, which is unknown.

Our definition of risk refers to an investment or group of investments.

Risk must be measured over some time horizon.

Risk must be measured relative to some benchmark, not in isolation.

If you want to know the risk associated with a specific investment strategy, the most appropriate

benchmark would be the risk associated with other investing strategies

Measuring Risk

Measuring Risk requires:

List of all possible outcomes

Chance of each one occurring

The tossing of a coin

What are possible outcomes?

What is the chance of each one occurring?

Is coin fair?

Probability is a measure of likelihood that an even will occur

Its value is between zero and one

The closer probability is to zero, less likely it is that an event will occur.

No chance of occurring if probability is exactly zero

The closer probability is to one, more likely it is that an event will occur.

The event will definitely occur if probability is exactly one

Probabilities can also be expressed as frequencies

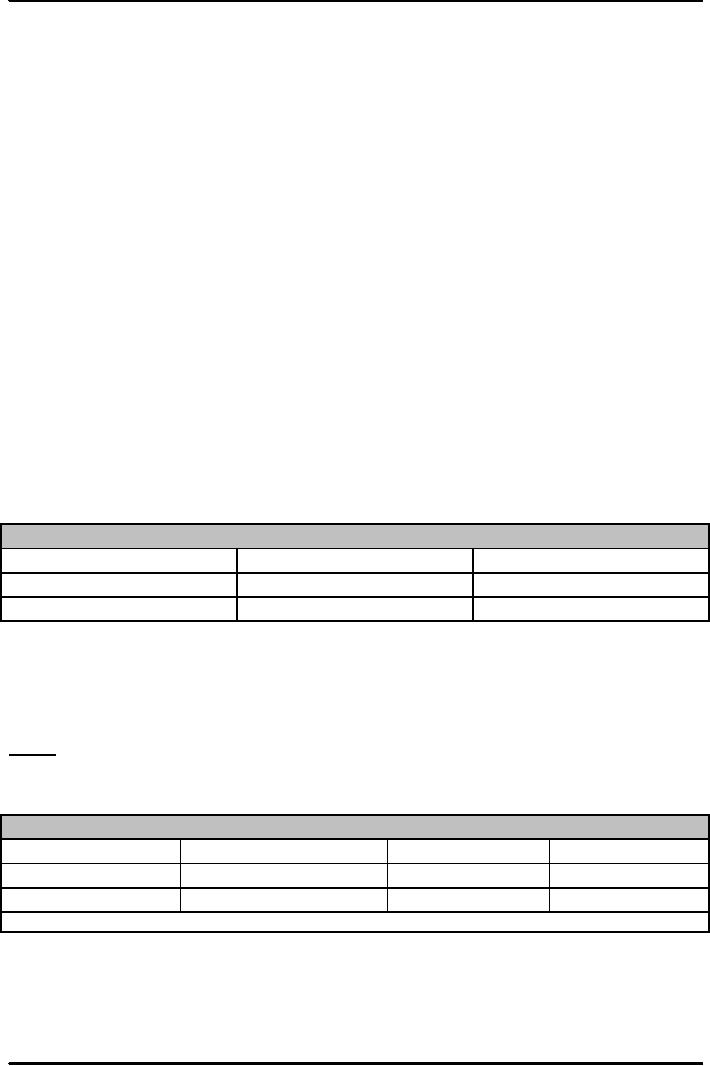
Table: A Simple Example: All Possible Outcomes of a Single Coin Toss

Possibilities

Probability

Outcome

1/2

Heads

1/2

Tails

We must include all possible outcomes when constructing such a table

The sum of the probabilities of all the possible outcomes must be 1, since one of the possible

outcomes must occur (we just don't know which one)

To calculate the expected value of an investment, multiply each possible payoff by its

probability and then sum all the results. This is also known as the mean.

Case 1

An Investment can rise or fall in value. Assume that an asset purchased for $1000 is equally likely to

fall to $700 or rise to $1400

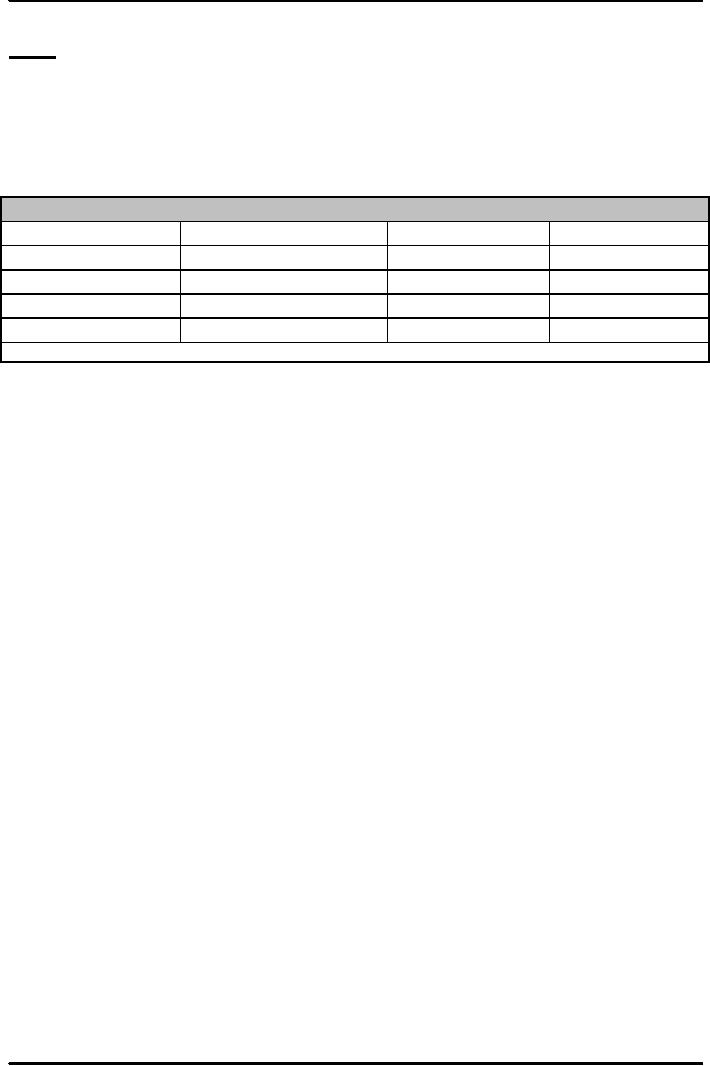
Table: Investing $1,000: Case 1

Possibilities

Probability

Payoff

Payoff ×Probability

1/2

$700

$350

1/2

$1,400

$700

Expected Value = Sum of (Probability times Payoff) = $1,050

Money & Banking MGT411

Expected Value = ½ ($700) + ½ ($1400) = $1050

Case 2

The $1,000 investment might pay off

$100 (prob=.1) or

$2000 (prob=.1) or

$700 (prob=.4) or

$1400 (prob=.4)

Table: Investing $1,000: Case 2

Possibilities

Probability

Payoff

Payoff ×Probability

0.1

$100

$10

0.4

$700

$280

0.4

$1,400

$560

$200

0.1

$2,000

Expected Value = Sum of (Probability times Payoff) = $1,050

Investment payoffs are usually discussed in percentage returns instead of in dollar amounts; this

allows investors to compute the gain or loss on the investment regardless of its size

Though both cases have the same expected return, $50 on a $1000 investment, or 5%, the two

investments have different levels or risk.

A wider payoff range indicates more risk.

Table of Contents: