 |
3
Branching
3.1.
COMPARISON AND
CONDITIONS
Conditional
jump was introduced in the
last chapter to loop for
the
addition
of a fixed number of array
elements. The jump was based on
the
zero
flag. There are many other
conditions possible in a program.
For
example
an operand can be greater
than another operand or it
can be
smaller.
We use comparisons and
boolean expressions extensively in
higher
level
languages. They must be available is
some form in assembly
language,
otherwise
they could not possibly be
made available in a higher
level
language.
In fact they are available
in a very fine and purified
form.
The
basic root instruction for
all comparisons is CMP standing
for
compare.
The operation of CMP is to subtract
the source operand from
the
destination
operand, updating the flags
without changing either the
source
or the
destination. CMP is one of the
key instructions as it introduces
the
capability
of conditional routing in the
processor.
A
closer thought reveals that
with subtraction we can check many
different
conditions.
For example if a larger
number is subtracted from a
smaller
number
then borrow is needed. The
carry flag plays the
role of borrow during
the
subtraction operation. And in this
condition the carry flag
will be set. If
two
equal numbers are subtracted
the answer is zero and
the zero flag will be
set.
Every significant relation
between the destination and
source is evident
from
the sign flag, carry
flag, zero flag, and
the overflow flag. CMP
is
meaningless
without a conditional jump immediately
following it.
Another
important distinction at this
point is the difference
between signed
and
unsigned numbers. In unsigned
numbers only the magnitude
of the
number
is important, whereas in signed
numbers both the magnitude
and
the
sign are important. For
example -2 is greater than -3 but 2 is
smaller
than 3.
The sign has affected our
comparisons.
Inside
the computer signed numbers
are represented in two's
complement
notation.
In essence a number in this
representation is still a number,
just
that
now our interpretation of this number
will be signed. Whether we
use
jump
above and below or we use
jump greater or less will convey
our
intention
to the processor. The jump
above and greater operations
at first
sight
seem to be doing the same
operation, and similarly
below and less
operations
seem to be similar. However
for signed numbers JG and JL
will
work
properly and for unsigned JA
and JB will work properly and
not the
other
way around.
It is
important to note that at
the time of comparison, the
intent of the
programmer
to treat the numbers as
signed or unsigned is not
clear. The
subtraction
in CMP is a normal subtraction. It is
only after the
comparison,
during
the conditional jump operation,
that the intent is conveyed.
At that
time
with a specific combination of flags
checked the intent is
satisfied.
For
example a number 2 is represented in a
word as 0002 while
the
number
-2 is represented as FFFE. In a byte
they would be represented as
02
and
FE. Now both have the
same magnitude however the
different sign has
caused
very different representation in
two's complement form. Now if
the
intent
is to use FFFE or decimal
65534 then the same
data would be placed
in the
word as in case of -2. In
fact if -2 and 65534 are
compared the
processor
will set the zero flag
signaling that they are
exactly equal. As
regards
an unsigned comparison the
number 65534 is much greater
than 2.
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
So if a JA is
taken after comparing -2 in
the destination with 2 in the
source
the
jump will be taken. If however JG is used
after the same comparison
the
jump will
not be taken as it will consider
the sign and with the
sign -2 is
smaller
than 2. The key idea is
that -2 and 65534 were
both stored in
memory
in the same form. It was
the interpretation that
treated it as a signed
or as an
unsigned number.
The
unsigned comparisons see the
numbers as 0 being the
smallest and
65535
being the largest with the
order that 0 < 1 < 2 ... <
65535. The signed
comparisons
see the number -32768 which
has the same
memory
representation
as 32768 as the smallest
number and 32767 as the
largest
with
the order -32768 < -32767
< ... < -1 < 0 < 1 < 2 < ... < 32767.
All the
negative
numbers have the same
representation as an unsigned number
in
the
range 32768 ... 65535
however the signed
interpretation of the
signed
comparisons
makes them be treated as negative
numbers smaller than
zero.
All
meaningful situations both
for signed and unsigned
numbers than
occur
after a comparison are
detailed in the following
table.
DEST =
SRC
ZF =
1
When
the source is
subtracted
from
the destination and both
are
equal
the result is zero
and
therefore
the zero flag is set.
This
works
for both signed
and
unsigned
numbers.
UDEST
< USRC
CF =
1
When an
unsigned source is
subtracted
from an unsigned
destination
and the destination
is
smaller,
borrow is needed which
sets
the carry flag.
ZF = 1 OR CF =
1
If the
zero flag is set, it
means
UDEST
≤
USRC
that
the source and
destination
are
equal and if the carry
flag is
set it
means a borrow was
needed
in the
subtraction and
therefore
the
destination is smaller.
CF =
0
When an
unsigned source is
UDEST
≥
USRC
subtracted
from an unsigned
destination
no borrow will be
needed
either when the
operands
are
equal or when the
destination
is
greater than the
source.
UDEST
> USRC
ZF = 0 AND CF =
0
The
unsigned
source
and
destination
are not equal if
the
zero
flag is not set and
the
destination
is not smaller since
no
borrow was taken.
Therefore
the
destination is greater
than
the
source.
SDEST
< SSRC
When
a signed source
is
SF ≠ OF
subtracted
from
a
signed
destination
and the answer is
negative
with no overflow than
the
destination is smaller
than
the
source. If however there is
an
overflow
meaning that the
sign
has
changed unexpectedly,
the
meanings
are reversed and a
32
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
positive
number signals that
the
destination
is smaller.
If the
zero flag is set, it
means
SDEST
≤
SSRC
ZF = 1 OR SF
≠
OF
that
the source and
destination
are
equal and if the sign
and
overflow
flags differ it means
that
the
destination is smaller
as
described
above.
SF =
OF
When
a signed source
is
SDEST
≥
SSRC
subtracted
from
a
signed
destination
and the answer is
positive
with no overflow than
the
destination
is greater than the
source.
When an overflow is
there
signaling
that sign has
changed
unexpectedly,
we interpret a
negative
answer as the signal
that
the destination is
greater.
SDEST
> SSRC
ZF = 0 AND SF =
OF
If the
zero flag is not set, it
means
that
the signed operands are
not
equal
and if the sign and
overflow
match
in addition to this
it
means
that the destination
is
greater
than the source.
3.2.
CONDITIONAL JUMPS
For
every interesting or meaningful
situation of flags, a conditional jump
is
there.
For example JZ and JNZ check
the zero flag. If in a
comparison both
operands
are same, the result of
subtraction will be zero and
the zero flag
will be
set. Thus JZ and JNZ can be
used to test equality. That
is why there
are
renamed versions JE and JNE
read as jump if equal or jump if not
equal.
They
seem more logical in writing
but mean exactly the same
thing with the
same
opcode. Many jumps are renamed with two
or three names for
the
same
jump, so that the appropriate
logic can be conveyed in
assembly
language
programs. This renaming is
done by Intel and is a
standard for
iAPX88.
JC and JNC test the carry
flag. For example we may
need to test
whether
there was an overflow in the
last unsigned addition or
subtraction.
Carry
flag will also be set if two
unsigned numbers are
subtracted and the
first
is smaller than the second.
Therefore the renamed
versions JB, JNAE,
and
JNB, JAE are there standing
for jump if below, jump if not
above or
equal,
jump if not below, and jump if
above or equal respectively.
The
operation
of all jumps can be seen
from the following
table.
JC
Jump if
carry
CF =
1
This
jump is taken if
JB
Jump if
below
the
last arithmetic
JNAE
Jump if
not above or equal
operation
generated a
carry
or required a
borrow.
After a CMP it
is
taken
if
the
unsigned
source is
smaller
than
the
unsigned
destination.
JNC
Jump if
not carry
CF =
0
This
jump is taken if
JNB
Jump if
not below
the
last arithmetic
JAE
Jump if
above or equal
operation
did
not
33
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
generated
a carry or
required
a borrow.
After a
CMP it is taken
if the
unsigned source
is
larger or equal to
the
unsigned
destination.
JE
Jump if
equal
ZF =
1
This
jump is taken if
JZ
Jump if
zero
the
last arithmetic
operation
produced a
zero in
its destination.
After a
CMP it is taken
if both
operands were
equal.
JNE
Jump if
not equal
ZF =
0
This
jump is taken if
JNZ
Jump if
not zero
the
last arithmetic
operation
did
not
produce
a zero in its
destination.
After a
CMP it is
taken if both
operands
were
different.
JA
Jump if
above
ZF = 0
AND
This
jump is taken
JNBE
Jump if
not below or equal
CF =
0
after a
CMP if the
unsigned
source is
larger
than
the
unsigned
destination.
JNA
Jump if
not above
ZF = 1
OR
This
jump is taken
JBE
Jump if
not below or equal
CF =
1
after a
CMP if the
unsigned
source is
smaller
than or equal
to
the
unsigned
destination.
This
jump is taken
JL
Jump if
less
SF ≠ OF
after a
CMP if the
JNGE
Jump if
not greater or equal
signed
source
is
smaller
than
the
signed
destination.
JNL
Jump if
not less
SF =
OF
This
jump is taken
JGE
Jump if
greater or equal
after a
CMP if the
signed
source is larger
than or
equal to the
signed
destination.
JG
Jump if
greater
ZF = 0
AND
This
jump is taken
JNLE
Jump if
not less or equal
SF =
OF
after a
CMP if the
signed
source is larger
than
the
signed
destination.
JNG
Jump if
not greater
ZF = 1
OR
This
jump is taken
JLE
Jump if
less or equal
after a
CMP if the
SF ≠ OF
signed
source
is
smaller
than or equal
to
the
signed
destination.
34
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
JO
Jump if
overflow.
OF =
1
This
jump is taken if
the
last arithmetic
operation
changed the
sign
unexpectedly.
JNO
Jump if
not overflow
OF =
0
This
jump is taken if
the
last arithmetic
operation
did
not
change
the
sign
unexpectedly.
JS
Jump if
sign
SF =
1
This
jump is taken if
the
last arithmetic
operation
produced a
negative
number in its
destination.
JNS
Jump if
not sign
SF =
0
This
jump is taken if
the
last arithmetic
operation
produced a
positive
number in its
destination.
JP
Jump if
parity
PF =
1
This
jump is taken if
JPE
Jump if
even parity
the
last arithmetic
operation
produced a
number
in
its
destination
that has
even
parity.
JNP
Jump if
not parity
PF =
0
This
jump is taken if
JPO
Jump if
odd parity
the
last arithmetic
operation
produced a
number
in
its
destination
that has
odd
parity.
JCXZ
Jump if CX is
zero
CX =
0
This
jump is taken if
the CX
register is zero.
The CMP
instruction sets the flags
reflecting the relation of
the destination
to the
source. This is important as when we
say jump if above, then what
is
above
what. The destination is
above the source or the
source is above the
destination.
The JA
and JB instructions are
related to unsigned numbers.
That is our
interpretation
for the destination and
source operands is unsigned.
The 16th
bit
holds data and not
the sign. In the JL and JG
instructions standing
for
jump if
lower and jump if greater
respectively, the interpretation is
signed.
The
16th bit holds the sign and
not the data. The
difference between them
will be
made clear as an elaborate
example will be given to explain
the
difference.
One
jump is special that it is not
dependant on any flag. It is JCXZ,
jump
if the
CS register is zero. This is
because of the special
treatment of the CX
register
as a counter. This jump is regardless of
the zero flag. There is
no
counterpart
or not form of this
instruction.
The
adding numbers example of
the last chapter can be a
little simplified
using
the compare instruction on
the BX register and
eliminating the need
for a
separate counter as
below.
35

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
Example
3.1
001
; a program to
add ten numbers without a separate
counter
002
[org
0x0100]
003
mov bx,
0
; initialize array index to
zero
004
mov ax,
0
; initialize sum
to zero
005
006
l1:
add
ax,
[num1+bx]
;
add
number to ax
007
add
bx, 2
;
advance bx to next
index
008
cmp
bx, 20
;
are we beyond the
last index
009
jne
l1
;
if not add next
number
010
011
mov
[total], ax
; write back
sum in memory
012
013
mov
ax,
0x4c00
; terminate
program
014
int
0x21
015
016
num1:
dw
10, 20, 30, 40, 50, 10, 20, 30,
40, 50
017
total:
dw
0
The
format of memory access is
still base + offset.
006
BX is
used as the array index as
well as the counter. The
offset of
008
11th
number will be 20, so as soon as BX
becomes 20 just after
the
10th
number has been added,
the addition is
stopped.
The
jump is displayed as JNZ in the debugger
even though we have
009
written
JNE in our example. This is because it is
a renamed jump
with
the same opcode as JNZ and
the debugger has no way
of
knowing
the mnemonic that we used
after looking just at
the
opcode.
Also every code and
data reference that we used
till now is
seen in
the opcode as well. However
for the jump instruction we
see
an
operand of F2 in the opcode
and not 0116. This will be
discussed
in
detail with unconditional jumps. It is
actually a short
relative
jump
and the operand is stored in
the form of positive or
negative
offset
from this
instruction.
With
conditional branching in hand,
there are just a few
small things left
in
assembly language that fills
some gaps. Now there is just
imagination and
the
skill to conceive programs
that can make you
write any program.
3.3.
UNCONDITIONAL JUMP
Till
now we have been placing
data at the end of code.
There is no such
restriction
and we can define data
anywhere in the code. Taking
the previous
example,
if we place data at the
start of code instead of at
the end and we
load
our program in the debugger. We
can see our data placed at
the start
but the
debugger is intending to start
execution at our data. The COM
file
definition
said that the first
executable instruction is at offset
0100 but we
have
placed data there instead of
code. So the debugger will try to
interpret
that
data as code and showed
whatever it could make up out of
those
opcodes.
We
introduce a new instruction called JMP.
It is the unconditional jump
that
executes regardless of the
state of all flags. So we
write an unconditional
jump as
the very first instruction
of our program and jump to the
next
instruction
that follows our data
declarations. This time 0100
contains a
valid
first instruction of our
program.
Example
3.2
001
; a program to
add ten numbers without a separate
counter
002
[org
0x0100]
003
jmp start
; unconditionally jump over
data
004
005
num1:
dw
10, 20, 30, 40, 50, 10, 20, 30,
40, 50
006
total:
dw
0
36
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
007
008
start:
mov
bx, 0
; initialize array index to
zero
009
mov
ax, 0
; initialize sum
to zero
010
011
l1:
add
ax,
[num1+bx]
;
add
number to ax
012
add
bx, 2
;
advance bx to next
index
013
cmp
bx, 20
;
are we beyond the
last index
014
jne
l1
;
if not add next
number
015
016
mov
[total], ax
; write back
sum in memory
017
018
mov
ax,
0x4c00
; terminate
program
019
int
0x21
JMP jumps
over the data declarations
to the start label
and
003
execution
resumes from there.
3.4.
RELATIVE ADDRESSING
Inside
the debugger the instruction
is shown as JMP 0119 and the
location
0119
contains the original first
instruction of the logic of our
program. This
jump is
unconditional, it will always be taken.
Now looking at the opcode
we
see
F21600 where F2 is the
opcode and 1600 is the
operand to it. 1600
is
0016 in
proper word order. 0119 is
not given as a parameter
rather 0016 is
given.
This is
position relative addressing in
contrast to absolute addressing. It
is
not
telling the exact address
rather it is telling how much forward
or
backward
to go from the current
position of IP in the current
code segment.
So the
instruction means to add
0016 to the IP register. At
the time of
execution
of the first instruction at
0100 IP was pointing to the
next
instruction
at 0103, so after adding 16 it
became 0119, the desired
target
location.
The mechanism is important to
know, however all
calculations in
this
mechanism are done by the
assembler and by the
processor. We just
use
a label
with the JMP instruction and
are ensured that the
instruction at the
target
label will be the one to be
executed.
3.5.
TYPES OF JUMP
The
three types of jump, near,
short, and far, differ in
the size of
instruction
and the range of memory
they can jump to with the
smallest
short
form of two bytes and a
range of just 256 bytes to
the far form of
five
bytes
and a range covering the
whole memory.
Short
Jump
Disp
EB
Near
Jump
EB
Disp
Low
Disp High
Far
Jump
EB
IP
Low
IP High
CS
Low
CS High
Near
Jump
When
the relative address stored
with the instruction is in 16 bits as in
the
last
example the jump is called a
near jump. Using a near jump we
can jump
anywhere
within a segment. If we add a large
number it will wrap around to
37

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
the
lower part. A negative
number actually is a large
number and works
this
way
using the wraparound
behavior.
Short
Jump
If the
offset is stored in a single
byte as in 75F2 with the
opcode 75 and
operand
F2, the jump is called a
short jump. F2 is added to IP as a
signed
byte.
If the byte is negative the
complement is negated from IP
otherwise the
byte is
added. Unconditional jumps can be
short, near, and far.
The far type
is yet
to be discussed. Conditional jumps can
only be short. A short
jump
can go
+127 bytes ahead in code
and -128 bytes backwards
and no more.
This is
the limitation of a byte in
singed representation.
Far
Jump
Far
jump is not position relative but is
absolute. Both segment and
offset
must be
given to a far jump. The
previous two jumps were used to
jump
within a
segment. Sometimes we may need to go
from one code segment
to
another,
and near and short jumps
cannot take us there. Far
jump must be
used
and a two byte segment and a
two byte offset are given to
it. It loads CS
wit the
segment part and IP with the
offset part. Execution
therefore resumes
from
that location in physical
memory. The three
instructions that have a
far
form
are JMP, CALL, and RET,
are related to program
control. Far
capability
makes
intra segment control
possible.
3.6.
SORTING EXAMPLE
Moving
ahead from our example of
adding numbers we progress to
a
program
that can sort a list of
numbers using the tools
that we have
accumulated
till now. Sorting can be
ascending or descending like if
the
largest
number comes at the top,
followed by a smaller number
and so on till
the
smallest number the sort
will be called descending. The
other order
starting
with the smallest number and
ending at the largest is
called
ascending
sort. This is a common
problem and many algorithms
have been
developed
to solve it. One simple
algorithm is the bubble sort
algorithm.
In this
algorithm we compare consecutive
numbers. If they are in
required
order
e.g. if it is a descending sort
and the first is larger
then the second,
then we
leave them as it is and if they
are not in order, we swap
them. Then
we do
the same process for
the next two numbers and so
on till the last two
are
compared and possibly
swapped.
A
complete iteration is called a
pass over the array. We
need N passes at
least
in the simplest algorithm if N is
the number of elements to be
sorted. A
finer
algorithm is to check if any
swap was done in this
pass and stop as
soon as
a pass goes without a swap.
The array is now sorted as
every pair of
elements
is in order.
For
example if our list of numbers is
60, 55, 45, and 58
and we want to
sort
them in ascending order, the
first comparison will be of 60 and 55
and
as the
order will be reversed to 55 and
60. The next comparison will
be of 60
and 45
and again the two will be
swapped. The next comparison
of 60 and 58
will
also cause a swap. At the
end of first pass the
numbers will be in order
of 55,
45, 58, and 60.
Observe that the largest
number has bubbled down
to
the
bottom. Just like a bubble at
bottom of water. In the next
pass 55 and 45
will be
swapped. 55 and 58 will not be
swapped and 58 and 60 will
also not
be
swapped. In the next pass
there will be no swap as the
elements are in
order
i.e. 45, 55, 58,
and 60. The passes will be
stopped as the last pass
did
not
cause any swap. The
application of bubble sort on
these numbers is
further
explained with the following
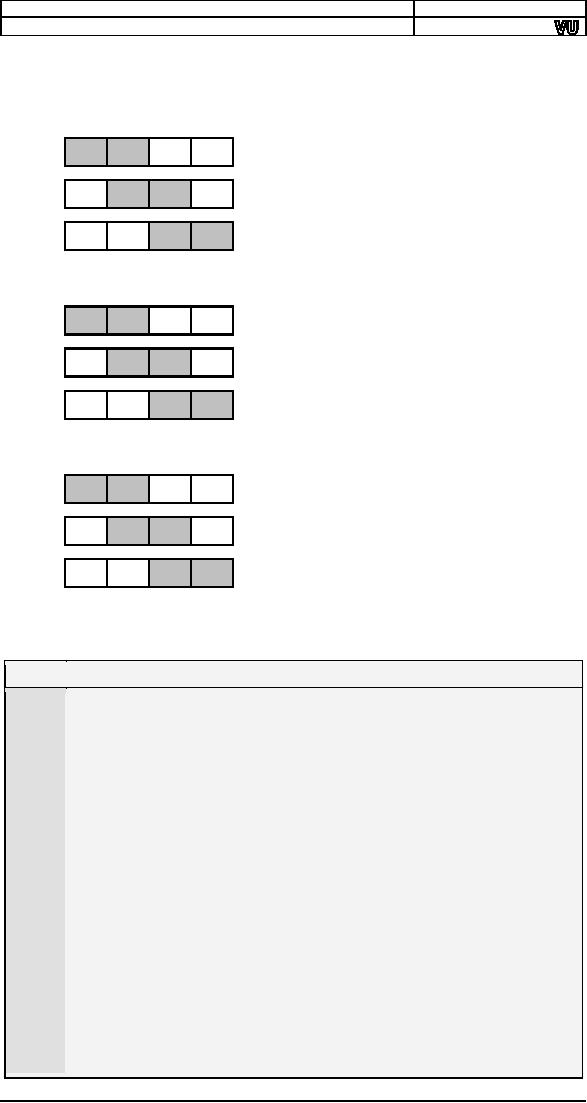
illustration.
38
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
State of
Data
Swap
Done
Swap
Flag
Pass
1
Off
Yes
On
60
55
45
58
Yes
On
55
60
45
58
Yes
On
55
45
60
58
Pass
2
Off
Yes
On
55
45
58
60
No
On
45
55
58
60
No
On
45
55
58
60
Pass
3
Off
No
Off
45
55
58
60
No
Off
45
55
58
60
No
Off
45
55
58
60
No more
passes since swap flag is Off
Example
3.3
001
; sorting a list of ten
numbers using bubble sort
002
[org
0x0100]
003
jmp
start
004
005
data:
dw
60, 55, 45, 50, 40, 35, 25, 30,
10, 0
006
swap:
db
0
007
008
start:
mov
bx, 0
; initialize array index to
zero
009
mov
byte [swap],
0
; rest swap flag
to no swaps
010
011
loop1:
mov
ax,
[data+bx]
; load number in
ax
012
cmp
ax,
[data+bx+2]
; compare with
next number
013
jbe
noswap
; no swap if
already in order
014
015
mov
dx,
[data+bx+2]
;
load second
element in dx
016
mov
[data+bx+2],
ax
;
store first number
in second
017
mov
[data+bx],
dx
;
store second
number in first
018
mov
byte [swap],
1
;
flag that a swap
has been done
019
020
noswap:
add
bx, 2
; advance bx to
next index
021
cmp
bx, 18
; are we at last
index
022
jne
loop1
; if not compare
next two
023
024
cmp
byte [swap],
1
; check if a
swap has been
done
025
je
bsort
; if yes
make another pass
026
027
mov
ax,
0x4c00
; terminate
program
028
int
0x21
39

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
The
jump instruction is placed to skip
over data.
003
The
swap flag can be stored in a
register but as an example it is
006
stored
in memory and also to extend
the concept at a later
stage.
One
element is read in AX and it is
compared with the next
element
011-012
because
memory to memory comparisons
are not allowed.
If the
JBE is changed to JB, not only
the unnecessary swap on
equal
013
will be
performed, there will be a major
algorithmic flaw due to
a
logical
error as in the case of
equal elements the algorithm
will never
stop.
JBE won't swap in the case
of equal elements.
The
swap is done using DX and AX
registers in such a way that
the
015-017
values
are crossed. The code
uses the information that
one of the
elements
is already in the AX
register.
This
time BX is compared with 18 instead of 20
even though the
021
number
of elements is same. This is
because we pick an
element
and
compare it with the next
element. When we pick the
9th element
we
compare it with the next
element and this is the
last comparison,
since
if we pick the 10th element
we will compare it with the
11th
element
and there is no 11th element in our
case.
If a
swap is done we repeat the
whole process for possible
more
024-025
swaps.
Inside
the debugger we observe that
the JBE is changed to JNA due to
the
same
reason as discussed for JNE
and JNZ. The passes change
the data in
the
same manner as we presented in our
illustration above. If JBE in
the
code is
changed to JAE the sort will
change from ascending to
descending.
For
signed numbers we can use
JLE and JGE respectively for
ascending and
descending
sort.
To
clarify the difference of
signed and unsigned jumps we
change the data
array
in the last program to
include some negative
numbers as well. When
JBE will be
used on this data, i.e. with
unsigned interpretation of the
data
and an
ascending sort, the negative
numbers will come at the end
after the
largest
positive number. However JLE will
bring the negative numbers
at the
very
start of the list to bring
them in proper ascending order
according to a
signed
interpretation, even though
they are large in magnitude.
The data
used is
shown as below.
data:
dw 60, 55, 45, 50, -40, -35,
25, 30, 10, 0
This
data includes some signed
numbers as well. The JBE
instruction will
treat
this data as an unsigned
number and will cater only
for the magnitude
ignoring
the sign. If the program is
loaded in the debugger, the
numbers will
appear
in their hexadecimal equivalent.
The two numbers -40 and
-35 are
especially
important as they are
represented as FFD8 and
FFDD. This data is
not
telling whether it is signed or
unsigned. Our interpretation will
decide
whether
it is a very large unsigned
number or a signed number in
two's
complement
form.
If the
sorting algorithm is applied on
the above data with JBE as
the
comparison
instruction to sort in
ascending order with
unsigned
interpretation,
observe the comparisons of
the two numbers FFD8
and
FFDD.
For example it will decide
that FFDD > FFD8 since
the first is larger
in
magnitude. At the end of
sorting FFDD will be at the
end of the list
being
declared
the largest number and
FFD8 will precede it to be the
second
largest.
If
however the comparison
instruction is changed to JLE and
sorting is
done on
the same data it works
similarly except on the two
numbers FFDD
and
FFD8. This time JLE declares
them to be smaller than every
other
number
and also declares FFDD <
FFD8. At the end of sorting,
FFDD is
40

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
declared
to be the smallest number
followed by FFD8 and then
0000. This is
in
contrast to the last example
where JBE was used. This
happened because
JLE
interpreted our data as signed
numbers, and as a signed
number FFDD
has
its sign bit on signaling
that it is a negative number in
two's complement
form
which is smaller than 0000
and every positive number.
However JBE
did
not give any significance to
the sign bit and included it
in the magnitude.
Therefore
it declared the negative
numbers to be the largest
numbers.
If the
required interpretation was of signed
numbers the result
produced
by JLE is
correct and if the required
interpretation was of unsigned
numbers
the
result produced by JBE is correct.
This is the very difference
between
signed
and unsigned integers in
higher level languages,
where the compiler
takes
the responsibility of making
the appropriate jump depending on
the
type of
integer used. But it is only at
this level that we can
understand the
actual
mechanism going on. In
assembly language, use of
proper jump is the
responsibility
of the programmer, to convey
the intentions to use the
data as
signed
or as unsigned.
The
remaining possibilities of signed
descending sort and
unsigned
descending
sort can be done on the
same lines and are
left as an exercise.
Other
conditional jumps work in the same
manner and can be studied
from
the
reference at the end.
Several will be discussed in more
detail when they
are
used in subsequent
chapters.
EXERCISES
1.
Which registers are changed
by the CMP instruction?
2. What
are the different types of
jumps available? Describe
position
relative
addressing.
3. If
AX=8FFF and BX=0FFF and
"cmp ax, bx" is executed, which of
the
following
jumps will be taken? Each part is
independent of others.
Also
give
the value of Z, S, and C
flags.
a. jg
greater
b. jl
smaller
c. ja
above
d. jb
below
4.
Write a program to find the
maximum number and the
minimum
number
from an array of ten
numbers.
5.
Write a program to search a
particular element from an
array using
binary
search. If the element is
found set AX to one and
otherwise to
zero.
6.
Write a program to calculate
the factorial of a number
where factorial
is
defined as:
factorial(x) =
x*(x-1)*(x-2)*...*1
factorial(0) =
1
41
Table of Contents:
- Introduction to Assembly Language Programming
- Addressing Modes: Data Declaration, Direct, Register Indirect , Offset Addressing
- Branching: Comparison and Conditions, Conditional ,Unconditional Jump
- Manipulations: Multiplication Algorithm, Shifting and Rotations, Bitwise Logical Operations
- Subroutines: Program Flow, Stack, Saving and Restoring Registers
- Display Memory: ASCII Codes, Display Memory Formation, Assembly Language
- String Instructions: String Processing, Clearing Screen, String Printing, Length
- Software Interrupts: Hooking an Interrupt, BIOS and DOS Interrupts
- Real Time Interrupts and Hardware Interfacing
- Debug Interrupts: Debugger using single step interrupt, breakpoint interrupt
- Multitasking: Concept, Elaborate, Multitasking Kernel as TSR
- Video Services: BIOS Video Services, DOS Video Services
- Secondary Storage: Storage Access Using BIOS, DOS, Device Drivers
- Serial Port Programming: Serial Communication
- Protected Mode Programming: VESA Linear Frame Buffer, Interrupt Handling
- Interfacing with High Level Languages: Calling Conventions, Calling C from Assembly
- Comparison: Motorolla 68K Processors, Sun SPARC Processor