NET PRESENT VALUE (NPV) AND INTERNAL RATE OF RETURN (IRR):RANKING TWO DIFFERENT INVESTMENTS

<< CAPITAL BUDGETING AND CAPITAL BUDGETING TECHNIQUES:Techniques of capital budgeting, Pay back period

PROJECT CASH FLOWS, PROJECT TIMING, COMPARING PROJECTS, AND MODIFIED INTERNAL RATE OF RETURN (MIRR) >>

Financial Management MGT201

Lesson 09

NET PRESENT VALUE (NPV) AND INTERNAL RATE OF RETURN (IRR)

Learning Objective:

In this lecture, we will discuss in detail the previous lecture topics that are

· Net Present value (NPV)

· Internal Rate of Return (IRR)

Net Present value (NPV):

The most important skill in this course is to understand the NPV equation and to calculate NPV

as reliably as possible. It is also the most important criteria in capital budgeting. It is very difficult to

calculate because different inputs used in Net present value equation are based upon a forecast, which

may or may not be accurate e.g. future cash flows and sales. Similarly, when we talk about the life of

the project, again we are estimating the duration of the project. We also have to choose subjectively the

discount rates to be used, including cost of capital, opportunity cost & required rate of return in the

calculation of Net present value. We will discuss how to choose the interest rate when we would talk

about risk. In NPV the idea is to bring back each cash flow to the present and then to add or subtract

them on present time. The project or investment, which is offering the highest NPV, gets the highest

rank.

Formula:

NPV = -Io + CFt / (1+i)t = -Io + CF1/(1+i) + CF2/(1+i) 2 + CF` /(1+i) 3 +..

Importance of NPV in terms of objectives of Financial Management:

The objective of FM is to maximize the shareholders wealth. Now, there is a direct link between

shareholder wealth maximization & NPV. It is mentioned earlier that the value of an asset is determined

by the future cash flows it generates. We used these future cash flows & discount them to present and

we call that the NPV. Hence, there is a direct link between NPV and future cash flows.

When the management of the company invest in the +ve NPV projects, they increase the economic

value added (E.V.A) and they also increase market value added (M.V.A). It should be clear by now that

when company invest in +ve NPV projects they brings in value to the company. Increase in the value of

the company implies increase in shareholders' wealth.

Example: Let us suppose that you invest Rs 100,000 in a Savings Certificate. After 1 Year you will

receive a coupon payment (or profit) of Rs 12,000 and you also reclaim your initial investment

(principal).

Solution:

Step 1: Identify the Variables: Io = Rs 100,000 CF1=Rs 12,000 Life = n=1year Required Rate

of Return = i =10% (assumed), Annual compounding. CF I1 = Rs 100,000

Here, we assume that i=10 because which is the opportunity cost as you can place that money in

a bank and can earn 10%. Do not forget that you get back your principal investment after 1 Year. This

is a positive cash flow and must be discounted back to the present just like any other future cash flow).

Step 2: Solve the NPV Equation

NPV =

-Io +

CF1 / (1+ i) +

CF I1 / (1+ i)

= -100,000 + 12,000/ (1+0.10) + 100,000/ (1+0.10)

= -100,000 +

10,909

90,909

= + Rs 1,818 NPV positive so investment acceptable

NOTE: PV = NPV + Io = 1,818 + 100,000 = Rs 101,818

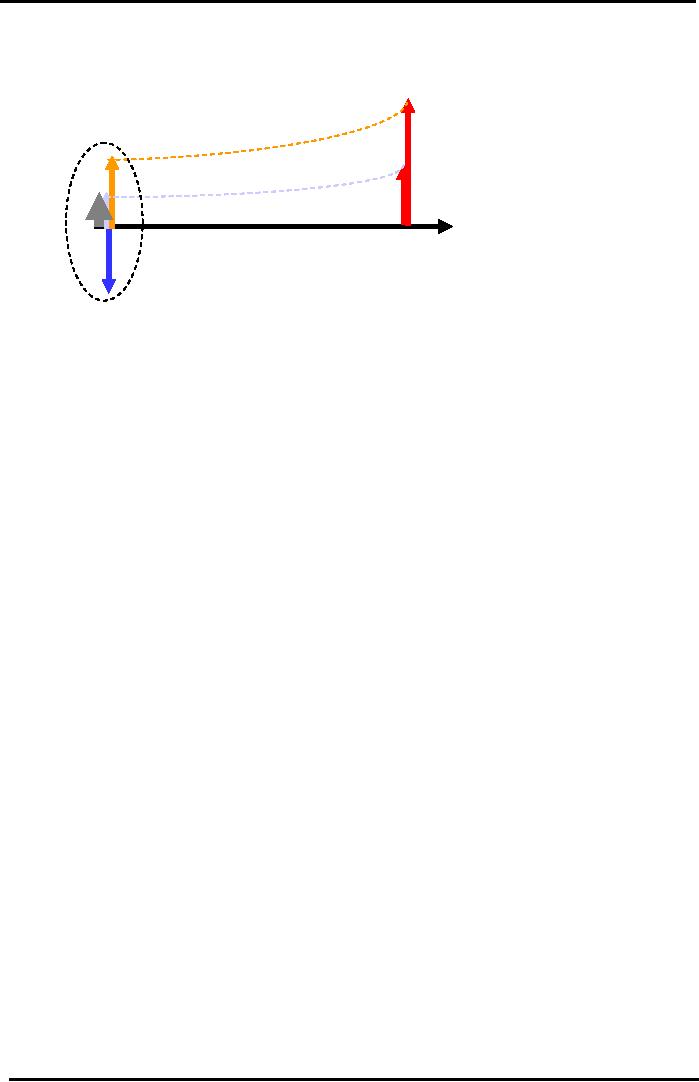
Financial Management MGT201

NPV Cash Flow Diagram

Savings Certificate Example

CFI1 = Rs

100,000

Rs 90,909

Rs 10,909

CF1= Rs

NPV =

12,000

i = 10%

Rs.1,818

Yr 0 (Today)

Yr 1

Io = Rs 100,000

In diagram initial downward sloping arrow shows the cash out flow and after one year two

upward pointing arrows (1. profit 2.return of initial investment) show the cash inflows.

Now let us talk about the Internal Rate of Return or IRR.

Internal Rate of Return or IRR:

IRR is a very commonly used criterion for capital budgeting. It is popular with the managers

because it gives a very simple answer in the form of annual percentage and you can compare it to the

inflation rate, cost of capital or financing or to the certain financial accounting ratios. The formula uses

trial & error method. We talk about the interpretation of IRR in the coming lectures.

The formula is similar to NPV

CFt / (1+IRR)t = -Io + CF1/(1+IRR) + CF2/(1+IRR) 2 + ..

NPV = 0 = -Io +

The value of i where NPV is zero is the value of IRR.

IRR represents the Break-even Return on Investment, but the important thing to remember is the

difference between IRR & NPV. When you are ranking different projects the ranking you get from NPV

may be different from the ranking you get from IRR, because, there is a major difference of

interpretation of i between NPV and IRR.

The difference is that in the case of NPV; we are externally specifying the discount rate based

on required rate of return. In NPV calculations, you have an idea of your opportunity cost for the capital

& you use it as `i'. As mentioned earlier that rate given by the banks on account is considered as

opportunity cost of your capital & you will invest in any project, which earns more than the rate offered

by a bank. However, in IRR i is derived from the cash flow pattern of the project. Remember that in

IRR project, we do not externally specify the interest rate but we calculated it from the cash flows.

Therefore, in the IRR it is what you called forecasted rate of return or an intrinsic rate of return. This is

an important difference to keep in mind between NPV & IRR.

Example:

Consider the Same Savings Certificate example for IRR calculation. The only difference is that

this time, we will not assume any value for "i" as we had done in the NPV calculation.

We set the NPV = 0 and solve the equation for "i" (or IRR).

NPV = 0 = -Io

+ [CF1 / (1+IRR)] + [CFI1 / (1+IRR)]

We add Rs 12,000 & Rs 10,000 as both appearing at the same time.

0 = -100,000 +

[(CF1 + CFI1) / (1+IRR)]

0 = -100,000 +

[(12,000+100,000) / (1+IRR)]

IRR= (112,000 / 100,000) - 1

(No need for trial & error because you have one variable & one unknown)

= 1.12 - 1.00 = 0.12 = 12 % per annum

Is that a good IRR, a high IRR or low IRR? These things we will discuss in this & in the next

lecture. Now, one very important thing, which you need to consider when you are evaluating an

investment proposal, is to look at NPV & to see how it changes as you change the discount rate .This is

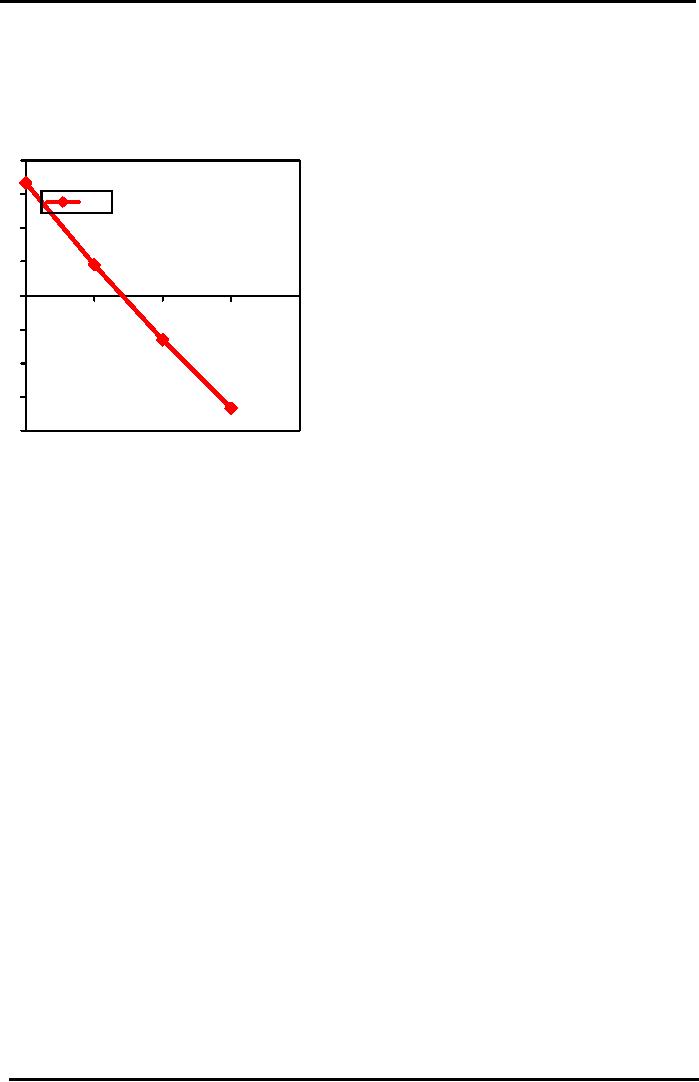
known as NPV Profile (See Fig.). Logically, when you increase the discount rate, the denominator

Financial Management MGT201

becomes larger & you net present value becomes smaller. What you find as a result is a downward

sloping line. The point where the NPV is zero would be the IRR for the project.

Graphical

IRR

Estimation

Using "NPV PROFILE"

8000

6000

NPV

4000

2000

IRR=12%

i=10%

i=15%

i=20%

-2000=5%

-4000

-6000

-8000

Using a low and a high value for "i", plot two points on the graph and extend the NPV line. Where the

line cuts the horizontal x-axis would be reflect the value of the IRR.

Use this Graphical Technique when:

1. The investment or project life is longer than 2 years.

2. Graphical technique very useful in IRR calculations as there are polynomial equations that are

time consuming to solve algebraically in terms of "i".

3. Comparing the NPV's of 2 or more investments, to study how sensitive the NPV's of the

different investments are to the discount rate "i"

The next issue is the ranking of different projects, which means given a choice of more than one

investment, which project is the best to invest in.

RANKING TWO DIFFERENT INVESTMENTS:

Which Investment is better?

Let us rank two Mutually Exclusive & Independent Investments using NPV and IRR criteria

Mutually Exclusive: means that you can invest in ONE of the investment choices and having chosen

one you cannot choose another.

Independent: implies that the cash flows of the two investments are not linked to each other

Example:

Let us consider two investment opportunities. One Investment is the Savings Certificate (which

we described earlier) and the second investment is a Bank Deposit of Rs 100,000 at 10% interest

compounded annually for two years.

NPV & IRR Numerical

Comparing the 2 Investments

Since we have calculated the NPV and IRR for the Savings Certificate, we would calculate the

NPV and IRR only for the Bank deposit rate.

Bank Deposit Example

FV = PV (1+i) n = 100,000 x (1.10)2 = 121,000

Financial Management MGT201

NPV = -100,000 + 10,000/ (1.1) + 11,000/ (1.1)2 + 100,000/(1.1)2 = 100,000 + 9,090 + 91,736 = + Rs

826

IRR: NPV = 0 = -100,000 + 10,000/ (1+IRR) + 111,000/ (1+IRR)2 ... by trial & error IRR = 10.5%

Compare the Investment 1 (Savings Certificate) to Investment 2 (Bank Deposit):

Bank Deposit

Savings Certificate

NPV (i=10% pa)

+ Rs 1,818

+ Rs 826

IRR

12% pa

10.5% pa

Savings Certificate appears to be a better investment because it offers both a higher NPV and a higher

IRR.

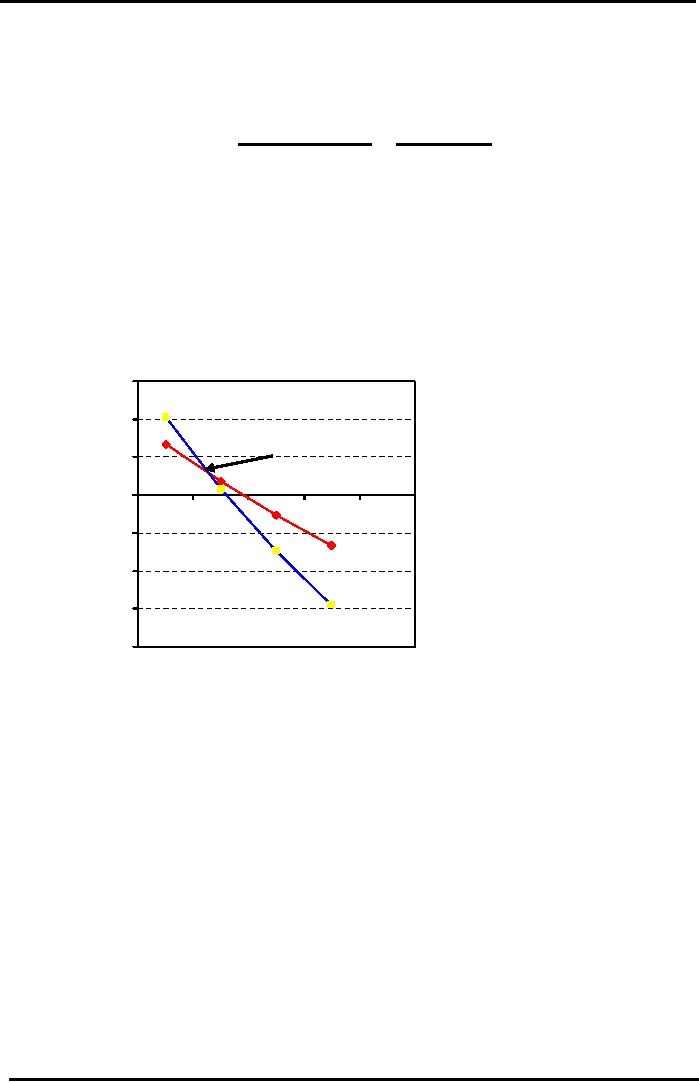
Graphical

Comparison

Investments

"CROSS-OVER IRR"

15000

10000

Cross Over Point

5000

i=10%

i=15%

i=20%

-5000

i=5%

-10000

-15000

-20000

The above diagram shows NPV Profiles of investments intersect at the Cross Over Point. Slope

of Bank Deposit investment is steeper because larger cash flows (Rs 111,000) are taking place later

in time (2 years instead of 1 year for Saving Certificates). Size of the Discounting Factor grows

exponentially with time so NPV graph falls much faster. The IRR at this Point is 8.8%.

At this point, the NPV of both the investments is equal at about +Rs 2,950

When IRR is less than 8.8% (Cross-over IRR) then the NPV of Bank Deposit is higher!

Investment Criteria

IRR Interpretation - How high is high.

Macro Aspects

Inflation:

An IRR, which is considered low for a medium inflation country like Pakistan, may be

considered high for a low inflation country like USA, Japan, and Singapore where inflation is below

5%.

Risk Free Rate of Return:

Recall our discussion from earlier lecture on Interest Rates and Money Markets.

In Pakistan, we use the Government T-Bill rate, which varies from 7% to 12% per annum

depending on the Money Market. Considering the risk-free rate of return the IRR on investment is

not very good. We will talk more about this after we study RISK.

Financial Management MGT201

Investment Criteria

IRR Interpretation (Micro Aspects)

ROA & ROE:

If the Investor has an existing running business that generates cash flows, then any new project

that matches or exceeds the returns of the existing business is worth considering.

Problem: ROA & ROE are Financial Accounting Ratios based on Net Income (not cash) &

Historical Cost or Book Value (not market value) whereas IRR is based on Cash and Forecasted Market

Value. The financial ratios are calculated based on the profit reported in the income statement, whereas

the IRR takes into account the cash flows rather than the accounting profit in the calculations.

Weighted Average Cost of Capital (WACC) or Hurdle Rate:

If the Investors an existing operating business that runs on borrowed money (or financing)

then the Investor (the borrower) bears the cost of interest, say 18% pa in Pakistan. Obviously, the rate of

cash generation should exceed the rate of interest payment. The IRR of a new project should exceed the

WACC. We will discuss this in detail when we study Capital Structuring. When IRR is above the

WACC, the excess return represents surplus that increases shareholders' wealth. The details on WACC

would be further discussed in Capital Structure determination.

Table of Contents: