DISCOUNTING CASH FLOW ANALYSIS, ANNUITIES AND PERPETUITIES:Multiple Compounding

<< PRESENT VALUE AND DISCOUNTING:Interest Rates for Discounting Calculations

CAPITAL BUDGETING AND CAPITAL BUDGETING TECHNIQUES:Techniques of capital budgeting, Pay back period >>

Financial Management MGT201

Lesson 07

DISCOUNTING CASH FLOW ANALYSIS, ANNUITIES AND PERPETUITIES

Learning Objectives:

After going through this lecture, you would be able to have an understanding of the following concepts.

· Discounted Cash Flows (DCF Analysis)

· Annuities

· Perpetuity

This lecture is continuation of the previous lecture's topics. In the previous lecture, we had

discussed the calculation of the Net Present Value (NPV) and the use of the value of interest rate or

Opportunity cost in the process. Bank Interest on the PLS Account represents the Minimum Opportunity

Cost of our investment. A good investment opportunity should, however, offer a higher return than the

Bank Interest rate. We also used the time & arrow diagram to show the cash flows forecast. In the

diagram, we used upward pointing arrow to represent the cash inflows & downward pointing arrow are

used to represent the cash outflows. You can simplify that diagram by arithmetically solving the upward

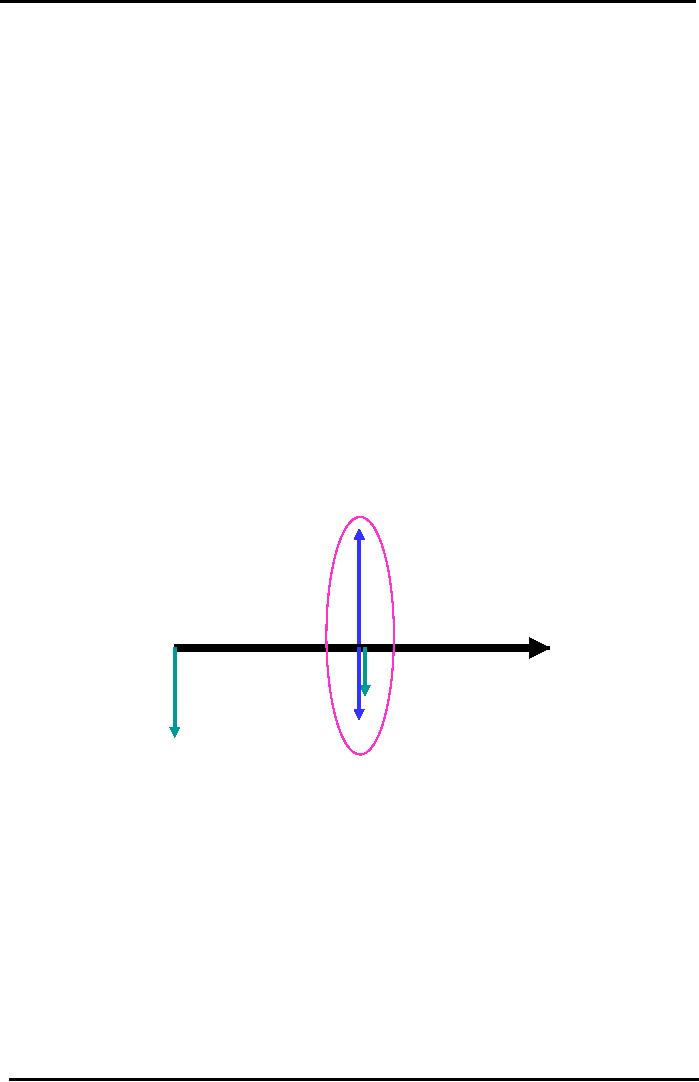
& down ward pointing arrows at same point in time by showing it with one arrow. (see Fig)

Cash Flow Diagram

Recap of Café Example

Use Downward Pointing Arrows to show Cash Outflows (Cash Payments or Expenses

or Investments). Use Upward Pointing Arrows to show Cash Inflows (Cash Receipts

ie. Cash Revenue or Income)

Receipts = Rs. 200,000

Year 1: 3 Cash Flow Arrows

at one point in time can be

simplified into 1 Net Cash

Flow Arrow: 200,000

50,000 30,000 = +120,000

Interest: 10% pa

Yr 0

Yr 1

Future Investment = Rs 30,000

Payments = Rs 50,000

Initial Investment = Rs 100,000

The arrows in time-and-arrow diagram can be added and subtracted when they are on same

point in time but when these arrows are at the different point of time these cannot be added or subtracted.

Now, let's talk about some common cash flow patterns the most common is called annuity.

Annuity:

An annuity is a series of fixed payments, which might be over a fixed number of years, or over

the lifetime of an individual, or both. The commonly known types of annuities we see are the monthly

rent, and monthly mortgage payments, or insurance premiums.

There are two types of annuities

1. Ordinary Annuity

An ordinary annuity, also known as deferred annuity, consists of a series of equal payments at the end of

each period.

2. Annuity Due

An annuity due consists of a series of equal payments at the beginning of each period.

Financial Management MGT201

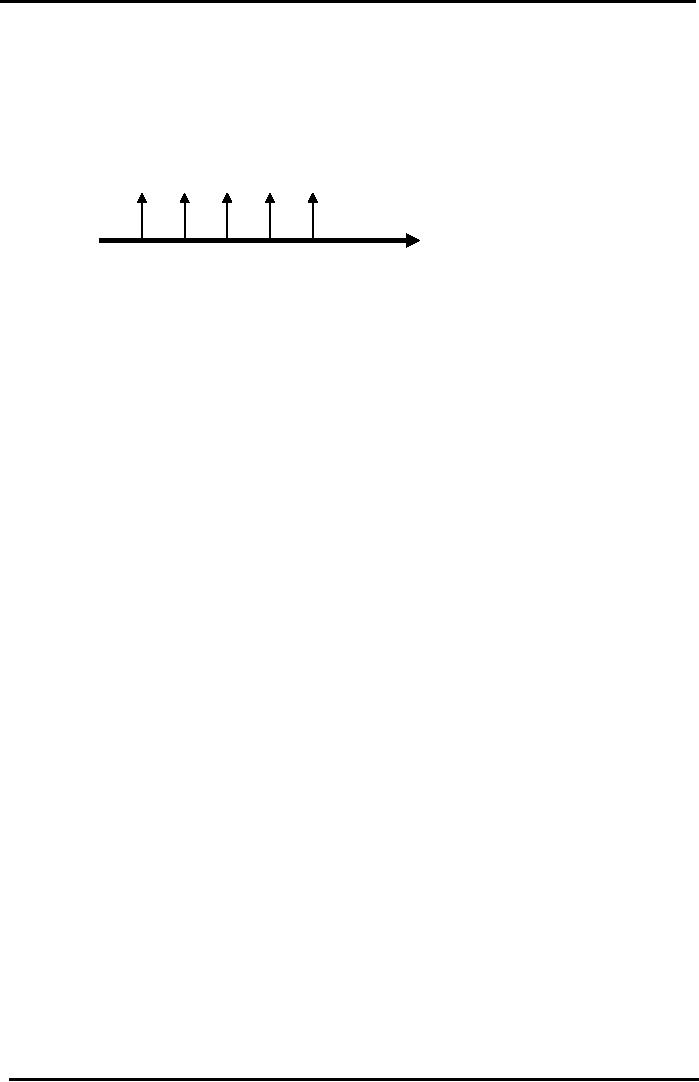
Value of Annuity depends on the Constant Cash Flows (CCF) (over a limited or finite

period of time) and the Discount Factor (which is different for Annual or Multiple

Compounding)

CCF

CCF CCF CCF CCF

Ordinary Five Year Annuity

Time Line (Years)

Yr 1 Yr 2

Yr 3 Yr 4 Yr 5

Annual Compounding (at end of every year):

FV = CCF (1 + i) n - 1

For example, the payment of Rs.10,000 as monthly rental to the land lord is an annuity which

gives birth to an annuity stream. Future value of an annuity can be seen as follows:

Future value of annuity =constant cash flows x (1+i) n-1/i

Where, i=interest rate

n=no. of years

We can write this formula in smaller compounded form which describes a compounding cycle given as

under:

Multiple Compounding:

Future Value of annuity =CCF (constant cash flow)*(1+ (i/m) m*n-1/i/n

Once we have calculated the future value of the annuity, it is very easy to calculate the present

value using the well-known interest rate formula.

Annual Compounding (at end of every year)

PV =FV / (1 + i ) n . n = life of Annuity in number of years

Multiple Compounding:

PV =FV / [1 + (i/m)] mxn

i = % interest per year

More than once per year i.e. Monthly (m =12), Quarterly (m=4), Six-monthly (m=2).

n = number of years

Now let's talk about another kind of cash flow pattern called perpetuity.

The difference between Annuity and Perpetuity is that the Perpetuity is an ongoing concern, it is never

ending stream of annuities, whereas an annuity is for a limited period.

Perpetuity:

"It is defined as an annuity with an infinite life making continual payments."

In real life, we see the example of perpetuity in the retirement plan. For Example, you might

plan to save a sufficient amount of money & invested in a particular security or investment that will give

you steady & consistent rate of return on every month or quarter and this represents a constant cash flow

amount that we can assume to go as long as you live. Since we are not sure how far we are going to live

and we make an infinite series of annuities the formula of Future value of Perpetuity is simpler than that

of annuity:

Future value of perpetuity=constant cash flow/interest rate

As we assume that, it is never ending and on going so time is irrelevant and is simply dropped

out of the equation.

Financial Management MGT201

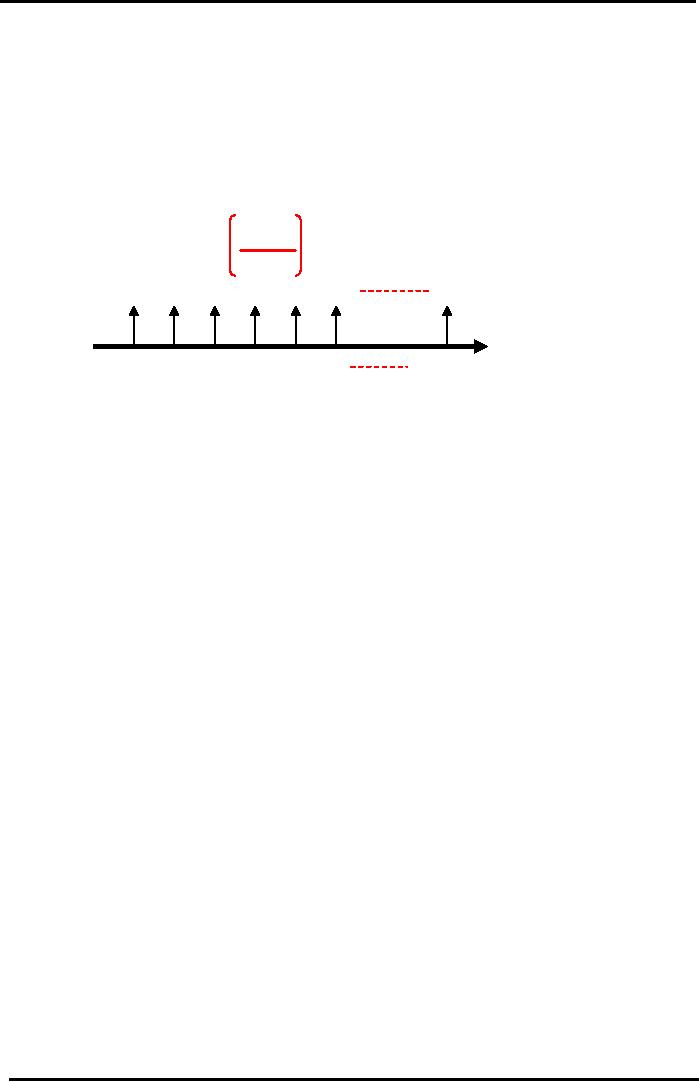
Common Cash Flow Patterns

Perpetuity

Perpetuity

Never-ending Annuity. It is a Perpetual or

Infinite stream of Constant Cash Flows

(CCF) at regular intervals.

PV = CCF

CCF

CCF CCF CCF CCF CCF

CCF

Infinity

Yr 1 Yr 2

Yr 3 Yr 4 Yr 5 Yr 6

Note: For Perpetuity whose CCF is growing at constant

annual growth rate % "g" : PV = CCF / (i - g)

Let's do a simple numerical example which will help us what an annuity calculation is like

Example:

Assume that we need to make a basic financial decision, whether to purchase a particular asset

or to get it on lease (installments).

A car has a Market Value today of Rs 150,000. If you get the car on Lease Financing, then you

are required to pay a fixed regular rental at a fixed interest rate to the Leasing Company. You are

allowed to use the car but the ownership of the car stays in the name of the Leasing Company until you

complete all your rental payments. The question is whether you should Lease the car or Buy it?

The Leasing Company quotes Rs 120,000 every year for 2 years in the form of Car Lease

Rental at a Nominal rate of interest (APR interest rate) of 20% pa. Then what is the total Future Value

you would have paid after 2 years? You would be paying approximately Rs 240,000 if you do not take

into account the time value of money.

Now we calculate the present value of the investment by using Time value of money concept.

First, we need to calculate the future value by using annuity formula

FV =CCF [(1+i) n - 1]/ i

=120,000[(1+0.2)2 -1]/0.2

= Rs 264,000 (yearly compounding)

If we deposit the amount annually in a bank at the rate of 20 percent, we would be able to get Rs

264,000 at the end of the second year. Now we will calculate what the present value of this future value

is going to be, and for this, we will use the old interest rate formula

PV = FV / (1+i) n

= 264,000 / (1+0.2)2

= Rs 183,333

The resulting amount is about Rs 33,000 more than what we would have originally paid if we

had bought the car rather than lease it

The above calculation, however, was not based on realistic assumptions because car lease

rentals are generally paid monthly, rather than annual payments. In fact, you pay Rs 10,000 per month

for 2 years. We use periodic interest rate (i/m). Now, what is the future value after 2 years? Our cash

flow diagram should present the monthly installments & not annual Payments.

Financial Management MGT201

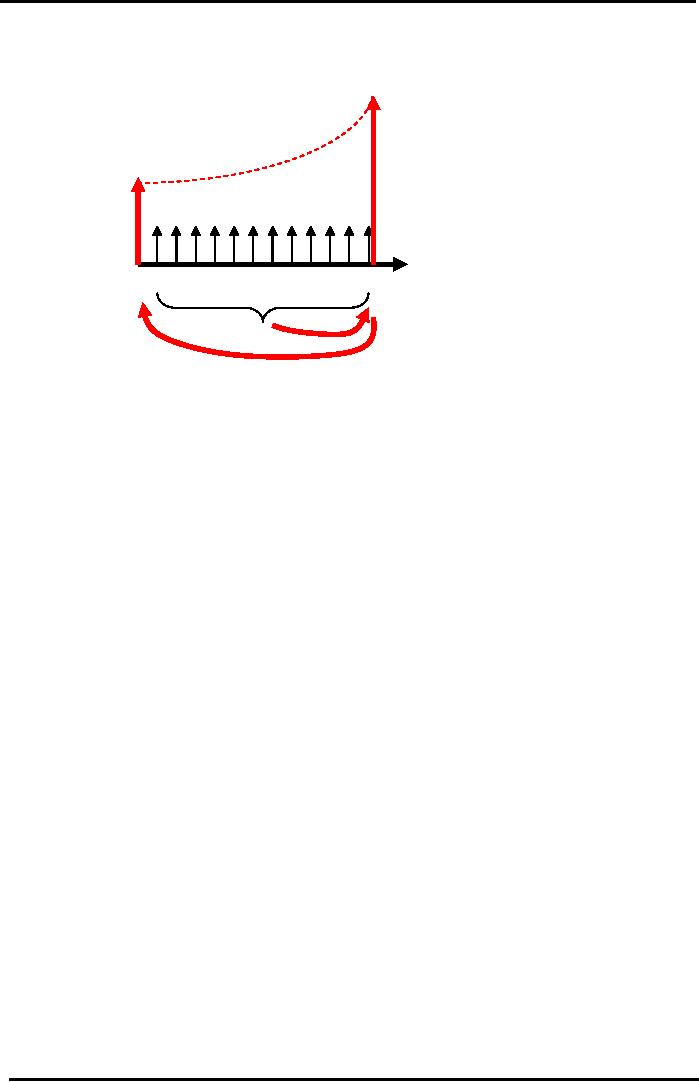
Monthly Lease Rentals Example

Annuity - Cash Flow Diagram

FV2 = Rs 292,150

PV = Rs 196,481

CCF = Monthly Rentals

= Rs 10,000

Interest = 20% pa

Time Line (Years)

Step 1: Bring All the Cash

Yr 0

Yr 1

Yr 2

Flows Forward to Year 2

(because formula is written

Step 1

in terms of FV).

Step2: Discount the

Step 2 (24 jumps back)

Combined Cash Flow at

Year 2 back to the Present

It can be argued that by paying a rental of 10,000 monthly, we are actually paying Rs 120,000

in a year, so there hardly any difference. But, by not realizing the difference, one is violating the time

value of money because cash flows occurring at different points of time cannot be subtracted or added.

It is the cardinal principle of Time value of money.

If we have to calculate the future value of the annuity on a monthly basis, we would use the

following formula.

=CCF X {[(1+i/m) nxm-1]/ (i/m)}

Now the m= 12 compounding cycle in a year

Putting the values in the formula, we obtain the result as under.

FV2=Rs 292,150

Now, we can calculate the present value of the future value of annuity

PV = FV / (1+i) n

=292150/(1+.2/12)2x12

=196,481

The present value of annuity can also be called the intrinsic value of the annuity.

The aforementioned technique allows us to compare the amount of money we are paying to

leasing company with the market value of car. It helps you to decide whether you should buy the car on

market price or to get it leased. The cost of leasing at 20% p.a. tell us that you have to pay 20% interest

& you have to pay more money in leasing as compare to the decision if you buy it .

Perpetuity Example - Retirement Planning

You would like to retire at the age of 60 and receive an income of Rs. 200,000 every year from

your Bank Account for as long as you live. How much money do you need to deposit in the Bank

Account offering 10% pa so that the Account will pay you Rs 200,000 of interest income every year

forever (even though you will not live forever)!

· PV = CCF / i = 200,000 / 0.10 = Rs 2,000,000

This also implies that you would be receiving Rs 200,000 every year for the rest of your life and

the money would neither finish nor decrease in amount. This would happen so, because what you would

be receiving at the end each year would be interest accrued on the investment that you have made. The

money that you are getting is not a part of the investment; instead, it is the yield on your investment.

This may sound like a `big idea' for making money, but in fact, it is not so. Inflation, a macroeconomic

syndrome erodes the value of money constantly. If the prevailing inflation rate is 5 percent, then your

real return on investment is not 10 percent. If we consider the real rate of return, which is interest rate

rate of inflation, you would see that you need to invest twice as much to guard yourself against inflation.

Financial Management MGT201

Another example for perpetuity is Consol Bonds. Consol Bonds were issued by the British

Government in 18th century to pay off the smaller bonds that were issued to fund the wars against

France. Since the purpose of the bond was to consolidate the past debts, it was named as Consol. These

bonds were just like other bonds issued by the government, with the difference that it had no maturity. It

implies that the holder of the bond was to receive regular interest payments for an endless period.

Now if we have to invest in such a bond we need to know the price or the present value of the

bond. Dividing the interest payment that a Consol bondholder would receive, by the interest rate, we can

find the present value of a Consol bond. Suppose that the interest rate is at 10 percent and the promised

interest payments to be received are £ 1,000 every year, the price of the bond can be calculated as under

· PV = CCF / i = 1,000/ 0.10 = £ 10,000

With this example, the discussion on discounted cash flows, annuities, and perpetuities is

concluded. We would study the capital budgeting techniques in the next lecture.

Table of Contents: