STOCK BETAS &RISK, SML& RETURN AND STOCK PRICES IN EFFICIENT MARKS:Interpretation of Result

<< STOCK BETA, PORTFOLIO BETA AND INTRODUCTION TO SECURITY MARKET LINE:MARKET, Calculating Portfolio Beta

SML GRAPH AND CAPITAL ASSET PRICING MODEL:NPV Calculations & Capital Budgeting >>

Financial Management MGT201

Lesson 25

STOCK BETAS &RISK, SML& RETURN AND STOCK PRICES IN EFFICIENT MARKS

Learning Objectives:

After going through this lecture, you would be able to have an understanding of the following

topics.

· Stock Betas and Risk

· SML & Required Returns (CAPM)

· Stock Prices in Efficient Markets

In the previous lecture, we have mentioned that the risk that is relevant in efficient markets where

the investors are sensible and rational is the market risk. This is because rational investors maintain

many stocks and they maintain diversified portfolio which contain stocks from different sectors and they

manage to eliminate their diversifiable risk and the only risk they faced is the market component of the

risk. However, this market component can not be eliminated and it will remain because markets do

fluctuate. Fluctuation in the Market Index (KSE 100 index) is a measure of Market Risk. This

fluctuation is caused by macro economic and socio political factors. Rational Investors in Efficient

Markets eliminate the Random Company-Specific Risk through Portfolio Diversification. So, in

Efficient Market the only Risk that remains is Market Risk. And so, the Price of Efficient Stocks is

based on Market Risk only. But the CAPM based on the fundamental principal that the rate of return for

the stock is directly proportional to the risk premium and the risk premium dependent on market risk

alone and not the total risk. Before going into details of SML we first go through the remaining topics

related to beta and its theoretical calculation based on standard deviation and covariance. We have

mentioned that beta of the stocks have tendency of stock to move with the market. It is experimentally

possible to calculate beta of the stock by monitoring the price or rate of return of the stock and at the

same time monitoring the market index in the same period of time & comparing that how the changes in

the stock market price relate to the changes in the stock market index. If you plot them on the graph

where you have expected return for stock on Y- axis and expected return from the stock market index

slope of the line from these points represent the beta

Stock Beta measures the Risk of a Stock Relative to the market.

Beta Stock A

= % Δ rA* / % Δ rM* = Slope of Regression Line. Regression Line uses

Experimental Data.

The formula that relates beta of the stock to the standard deviation is as follows

Beta Stock A = Covariance of Stock A with Market / Variance of Market

= σ A σ M ρ AM / σ 2 M

(Covariance Formula based on Probability & Statistical Portfolio Theory) Links Stock Beta

(Market Portion of Risk) to Stock Standard Deviation (Total Single Stock Risk).

Simplified formula:

= σ A ρ AM / σ M = market risk

Theoretical Beta Example:

Suppose you have Analyzed the Historical Time Data for (1) Movements of the Price (or Return) of

a Stock A and (2) Movements in the Value of the Stock Index.

You then Apply Simple Probability Formulas to compute the following Standard Deviations:

σ A = 30% (Stock A's Total Risk or Standard Deviation)

σ M = 20% (Stock Market Index Standard Deviation or Risk)

ρ AM = + 0.8 (Correlation between Stock A and the Market Index)

Compute the Theoretical Beta of Stock A:

Stock A Beta = 30% (0.8) / 20% = 24% / 20% = 1.2

108

Financial Management MGT201

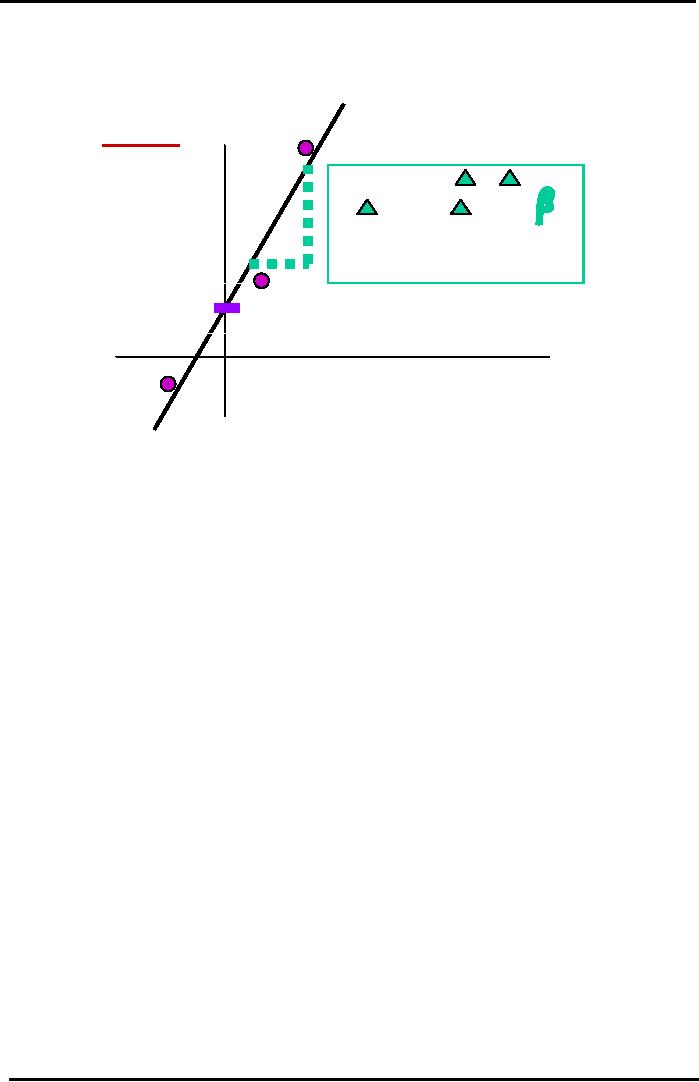
Calculating Stock Beta Graphically

Linear Regression through Annual Data Points for 3 Years.

CALCULATION OF BETA

Year 2

BASED ON EXPERIMENTAL

Expected

DATA OR OBSERVATION

Return on

Slope = Beta = Y / X

Stock A

= % rA* / % rM* =

(Historical) %

A =Risk Relative to Market =

rA* - rRF

(rA* - rRF) / (rM* - rRF)

Y-Intercept =

Year 1

Alpha =

Company Specific Risk

rM* - rRF

Expected Return on KSE 100 Market Index

Year 3

(Historical) %

The beta of 1.2 shows that stock is relatively more risky then the market and if the market

moves up by 10% this stock will move up by 12%.

If all the points of the stock lie on the straight line then stock does not have any diversifiable risk. The

difference between the actual data point and the point which vertically lies above or below the point is

representative of the error which is representative of the company's risk attached to any stock.

Now we can put together the two concepts which we studied up till now that is company's

specific risk and the second concept of regression line and the distance between data line and actual

point of the company's risk. Now, we can come up with the total definition of total risk variances.

Total variance risk formula:

Total Risk of Stock A in terms of Variance (= Std Dev 2)

Total Risk = Market Risk + Random Specific Unique Risk

σ2A

β2A σ2 M

+ σ 2 A-Error

Visualizing the Variance Risk Formula on the Regression Line

If a Stock is Part of a Totally Diversified Portfolio then its Company Risk = 0. Therefore Total Risk

= Market Risk. And the Stock points will lie exactly on the Regression line.

If a Stock is a Single Investment then it carries Company Specific or Diversifiable or Random Risk.

This means that its points will not lie on the Regression line. The extent to which the points are

scattered away is a measure of the Variance Error Term (last term in the formula)

109

Financial Management MGT201

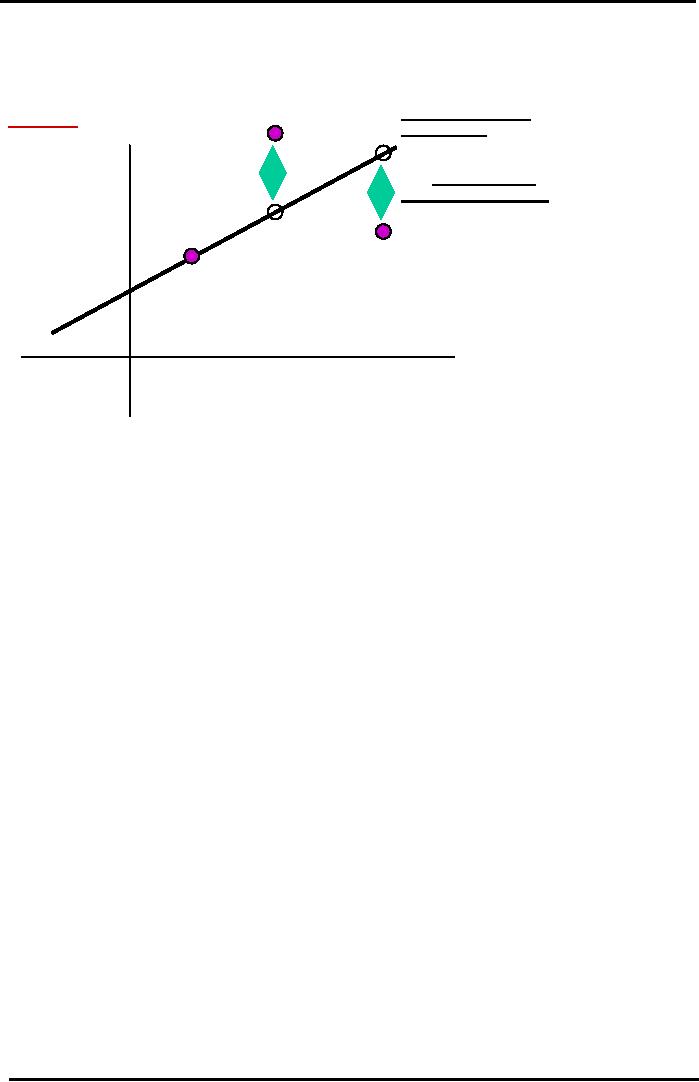
How Efficiently Priced is Stock A?

Regression (Beta) Line for Stock

IF STOCK A WERE

Expected Return

EFFICIENT, ALL

on Stock A

Error =

POINTS WOULD LIE

(Historical) %

Measure of

ON A STRAIGHT LINE

Company -

AND TOTAL RISK =

rA* - rRF

Specific Risk

MARKET RISK ONLY

Error =

of Stock A

Measure of

Company -

Specific Risk

of Stock A

rM* - rRF

Expected Return on KSE 100 Market Index (Historical) %

Variance Risks Example:

If the Market Risk = 20% and Stock A's Beta = 1.5 then what is the Relevant Market Risk

Component of Stock A?

Stock A's Market Variance = Beta A2 x Market Variance = 1.52 x (20%) 2 = 2.25 x 400% =

900% (Variance)

So the Stock A's Market Risk (in Standard Deviation terms) = Square Root of Variance = 30%

= Beta A σ M

Note that Total Risk of Stock A can be calculated directly by calculating the Standard Deviation of

the Possible Future Returns. That was the first Risk Formula we studied in Risk Theory.

Suppose Total Risk = 35%. Then Company Specific or Diversifiable or Random Risk of Stock A =

Total Risk - Market Risk = 35% - 30% = 5%.

So 86% (= 30/35 x 100) of Stock A's Total Risk is Market Risk - quite likely that Stock A is Part of

a well Diversified Portfolio or Mutual Fund.

Security Market Line (SML) :

Straight Line Model is for Beta Risk and Required Return. Similar to the Relationship for the 2-

Stock Portfolio with Ro>0 Beta Risk is Directly Proportional to Required Return. The Investors require

an extra Return which exactly compensates them for the extra Risk of the Stock relative to the Market.

SML Linear Equation for the Required Return of any Stock A:

rA = rRF + (rM - rRF ) β A

In the above formula

rA = Return that Investors Require from Investment in Stock A.

rRF = Risk Free Rate of Return (i.e. T-Bill ROR).

rM = Return that Investors Require from Investment in an Average Stock (or the Market

Portfolio of All Stocks where β M = + 1.0 always).

β A = Beta for Stock A. (rM - rRF ) β A = Risk Premium or Additional Return Required in

Excess of Risk Free ROR to compensate the Investor for the Additional Market Risk of the Stock

Required Rate of Return,

Risk Premium & Market Risk:

SML Model for Efficient Markets establishes a Straight Line relationship (or Direct Proportionality)

between a Stock's Required ROR and its Risk Premium.

rA = rRF + (rM - rRF ) A

A Stock's Risk Premium depends on its Market Risk Portion (and not the Total Risk)

110

Financial Management MGT201

In Efficient Markets, Market Price of a Stock is based on Required Return which depends on

Risk Premium which depends on Stock's Market Risk Component (and not the Total Risk).

Stock Prices in Efficient Markets:

A Single Stock Investor who owns No Stocks and wants to buy a Share A will have to face

more Risk (Market Risk + Specific Risk) than a Rational Fully Diversified Investor. The Single

Stock Investor will want to buy the Stock at a lower price to compensate him for the higher risk.

However, Efficient Markets do not price stocks based on Single Stock Investors who want

compensation for taking on Unnecessary Company-Specific Risk which they should have

diversified away.

Efficient Markets price the Stocks based on their Market Risk Component only. So, Efficient Stock

Prices are based on Rational Investors holding Diversified Portfolios of many stocks.

SML - Numerical Example:

Calculate the Required Rate of Return for Stock A given the following data:

β A = 2.0 (i.e. Stock A is Twice as Risky as the Market)

rM = 20% pa (i.e. Market ROR or ROR on a Portfolio consisting of All Stocks or ROR on

the "Average Stock")

rRF = 10% pa (i.e. T-Bill ROR)

SML Equation (assumes Efficient Stock Pricing, Risk, and Return)

rA = rRF + (rM - rRF ) β A .

= 10% + (20% - 10%) (2.0) = 30%

Interpretation of Result:

Investors require a 30% pa Return from Investment in Stock A. This is higher than the

Market ROR because the Stock (Beta = 2.0) is Riskier than the Market (Beta = 1.0 always).

If Required Return (30%) is higher than Expected Return (20%) it means that Stock A is

Unlikely to Achieve the Investors' Requirement and Investors will NOT invest in Stock A.

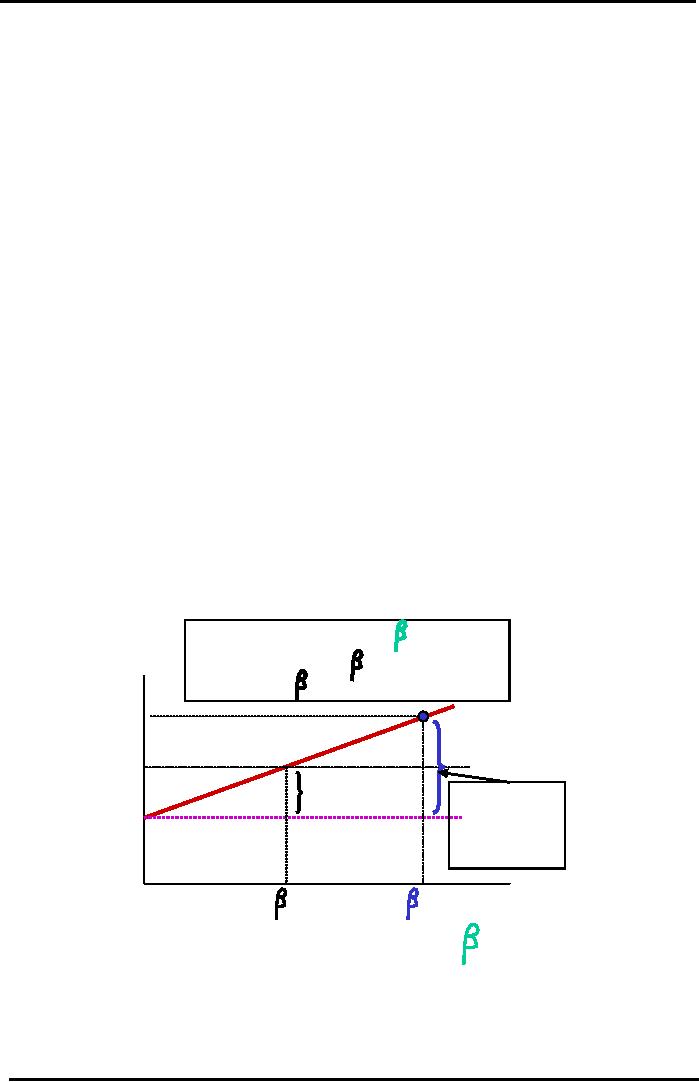
Security Market Line (SML)

For Market of Efficient Stocks

rA = rRF + (rM - rRF ) x

Required

y = c + mx where x = and m = Slope =

(rM - rRF) / ( M - 0) = (rM - rRF) /1

Return (r*)

rA= 30%

Security Market Line

rM= 20%

Market Risk

Premium for

Risky Stock A's

Avg Stock =

rRF= 10%

Total Risk

10%

Premium =

30-10 = 20%

A =+ 2.0

M =+ 1.0

Beta Risk (

)

111

Table of Contents: