EFFICIENT PORTFOLIOS, MARKET RISK AND CAPITAL MARKET LINE (CML):Market Risk & Portfolio Theory

<< PORTFOLIO RISK ANALYSIS AND EFFICIENT PORTFOLIO MAPS

STOCK BETA, PORTFOLIO BETA AND INTRODUCTION TO SECURITY MARKET LINE:MARKET, Calculating Portfolio Beta >>

Financial Management MGT201

Lesson 23

EFFICIENT PORTFOLIOS, MARKET RISK AND CAPITAL MARKET LINE (CML)

Learning Objectives:

After going through this lecture, you would be able to have an understanding of the following

topics.

· Efficient Portfolios,

· Market Risk & CML

First we recap the important concepts which we have studied in previous lectures. Portfolio theory

is looking at the relationships between the risk and return for portfolios, especially for diversified

portfolios.

Total Stock Return = Dividend Yield + Capital Gain Yield

You should recall this from the Gordon formula that we learnt in the share valuation.

We spoke about the total risk for the stock and we said that it is equal to the company's risk plus the

market risk.

Total Risk = Diversifiable Risk + Market Risk

We mentioned that on the basis of experimental studies that if we invest in many stocks which are

not correlated to each other then it is possible to reduce overall risk for your investment as a whole. We

called this portfolio or collection of stocks. 7 Stocks are a good number for diversification & 40 Stocks

are enough for eliminating Company Risk & Minimizing Total Risk.

Now, in the portfolio theory model which we are going to discuss the major assumption is that the

rational investors in the market place maintain diversified portfolios. We discuss in the previous lecture

about calculating expected return on the portfolio and we mentioned that it is simply the weighted

average of return of each stock in the portfolio. The formula

2-Stock Portfolio's Expected Return = rP * = xA rA + xB rB

2-Stock Portfolio Risk Formula

Sd= √ X A2 σ A 2 +XB2 σ B 2 + 2 (XA XB σ A σ B

AB)

It is mentioned in the previous lecture that we can calculate the risk of larger portfolio using the

matrix approach

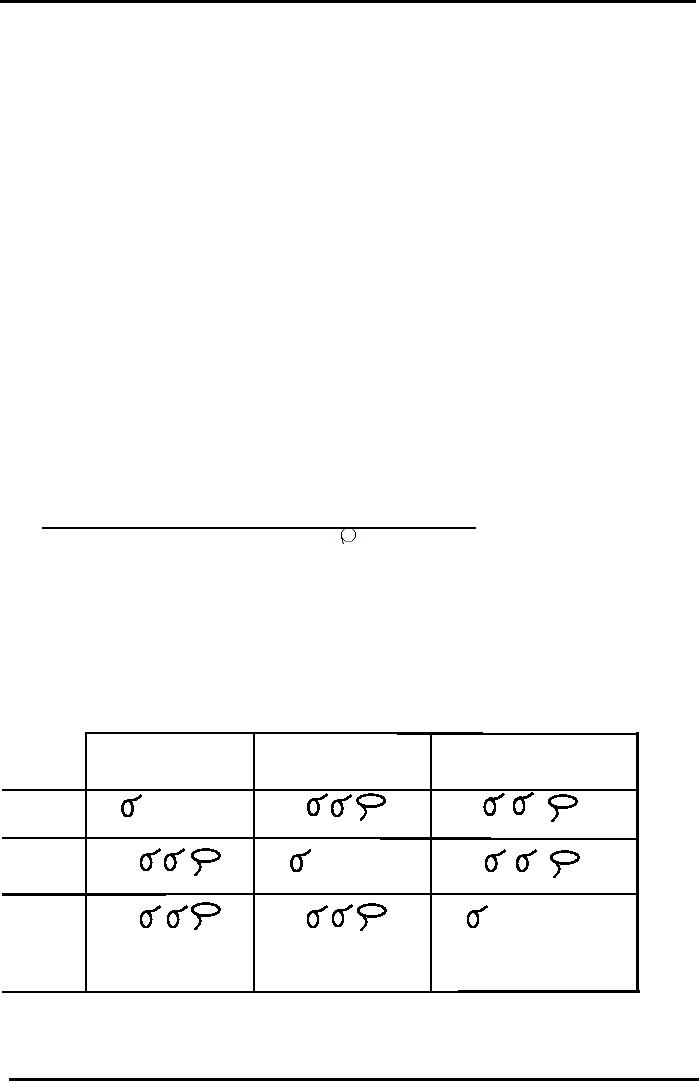
Matrix for Calculating Portfolio Risk: Covariance Terms (Non-Diagonal Boxes) measures (1)

Magnitude of movement (Standard Deviation) and (2) Closeness of movement (Correlation

Coefficient) between any two stocks in the portfolio.

3-Stock Portfolio Risk Formula

3 x 3 Matrix Approach

Stock A

Stock B

Stock C

XA2

Stock

XA XB

XA XC

XB2

Stock

XB XA

XB XC

XC2

Stock

XC XA

XC XB

To compute the Portfolio Variance for a 3-Stock Portfolio, just add up all the terms in every

box. To compute the Portfolio Risk (Standard Deviation), simply take the Square Root of the Variance.

Financial Management MGT201

You can extend this Matrix Approach to calculate the Risk for a Portfolio consisting of any

number of stocks.

·Terms in Boxes on Diagonal (Top Left to Bottom Right) are called "VARIANCE" terms associated

with individual magnitude of risk for each stock.

·Terms in all other (or NON-DIAGONAL) Boxes are called "COVARIANCE" terms which account

for affect of one stock's movement on another stock's movement. These represent the magnitude or size

of the movement between the two stocks. There are two parts for this covariance terms

·One of the two covariance terms for two stock portfolios is XA XB σ A σ B

AB.

Both standard deviation and covariance are important to calculate the size of the movement of

both stock A and B. In other words, if covariance is large then a pair of stock moves a lot and they also

move together. Correlation coefficient is the measure that how closely they move Standard deviation

tells us that how much they move.

We have discussed in the previous lecture about the efficient portfolio map and the efficient

frontier. If we plot the risk and return for the portfolio whose correlation coefficient is negative then we

come up with a hook shape curve and it tells us that it is possible to increase the return on portfolio & at

same time reduce the risk which is ideal because the objective is to maximize the return and to minimize

the risk. But in conclusion of last lecture we said that there is a whole line with infinite number of points

that represents an efficient frontier and every single combination or mix of the portfolio on this line

represents an efficient combination. But this does not help us very much why because we do not know

which one of these mix is the best. So, the first ting we are going to figure out is that what optimal mix

of the portfolio is. The starting point to figure out this is to realize that if you have a portfolio of stocks

then every investor have access to another portfolio and that portfolio is the portfolio of T bills and we

are going to assume that every body have the option of investing in the T-Bills that give them the risk

free rate of return. For Pakistan, we consider that figure to be 10%.So; this is the starting point to figure

out that what is the optimal portfolio mix is. The realization that if your portfolio is giving you the

return which is less then risk free rate of return then why would you investing in that portfolio and you

would choose to invest in T-bills. By using this understanding, let's take another look on risk and return

portfolio frontier model and see that how we can use this fact to find the optimal portfolio mix and we

take look at 3 stock portfolio consisting of stock A, B and C and added to that we will give ourselves the

option of investing in a T-bill portfolio wherever stocks are not providing sufficient return. So, if we

look at the e efficient portfolio map you will see that Portfolio risk is on X- axis and the portfolio

return on Y- axis.

Financial Management MGT201

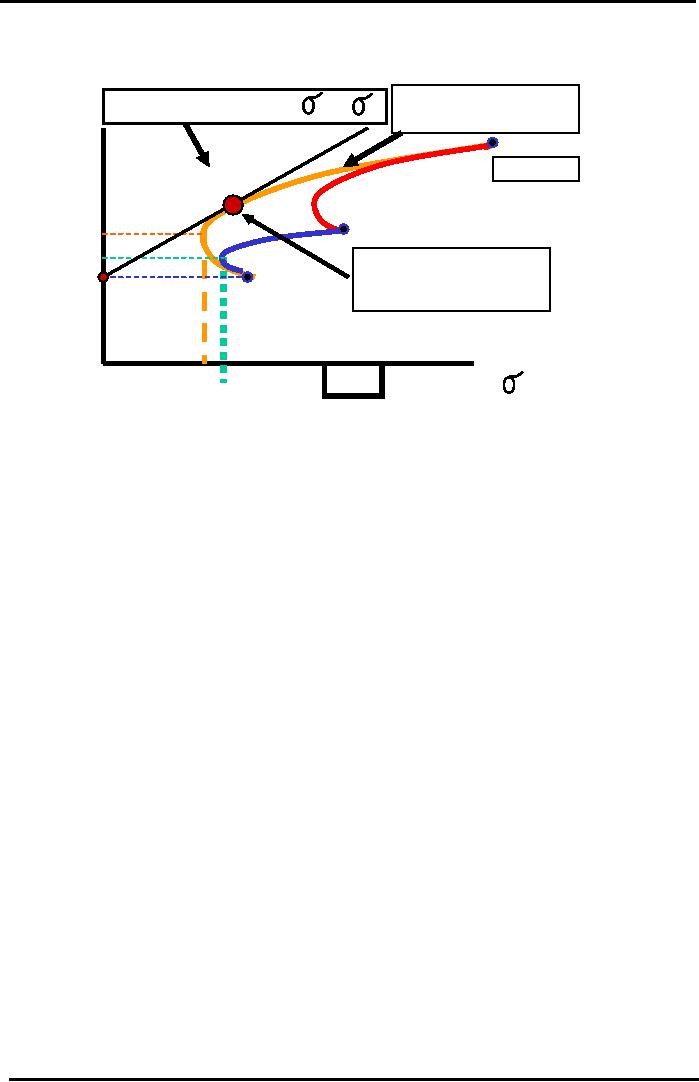
Picking Most Efficient Portfolio

Capital Market Line (CML) & T-Bill Portfolio

P Efficient Frontier

rP* = rRF + [ (rM - rRF) / M ]

rP*

for 3-Stock Portfolio

Portfolio

Capital Market Line

Stock C

Return 30%

"The Parachute"

Stock A

20%

Optimal Portfolio Mix

(50%A, 30% B, 20%C) if

10%=

Stock B

rRF

Risk Free T-Bill ROR = 10%

40%

20%

2.5%

Portfolio with Negative

3.4%

Portfolio Risk

or Zero Correlation

Coefficient

The efficient frontier for the 3 stock portfolio is the overarching largest hook shaped curve and

also remember that closed combination of the all the hook shaped curves forms a parachute like

shape and any one of the points inside that parachute is a possible mix or combination of different

stocks that you can have in your portfolio. However, the most efficient combinations lie on the

efficient frontier line and the next logical step we are going to take is to figure out what is the best

point on the efficient frontier. As it is mentioned that we will assume that we have access to T- bill

portfolio which offers a risk free rate of return of 10% and that will be the starting point of our

capital market line (CML).wherever this line if you extend from the 10 % point from y-axis touches

the efficient frontier line and is tangent to it is the point for the "Optimal Portfolio Mix." This point

is shown as a large dot in the above figure. If you look at the location of this large dot on the

efficient frontier you can see that it lies closer to the Stock B and Stock A. Therefore, there is larger

percentage of stock A and B in this optimal portfolio mix. Approximately, the optimal portfolio mix

consist of 50% Stock A, 30% Stock B, and 20% Stock C. It is important to remember that we have

the option of investing in the T-bill portfolio which offers a risk free rate of return

And the expected rate of return is 10%.Therefore, if the returns on this portfolio decrease 10%

then the investor will invest in the risk free T bills portfolio. Whichever portfolio offers lowest

coefficient of variation is the better portfolio. The CML represents different combinations that you

can pick in the risk free as well as stock portfolio. Thus CML represents combination of efficient

portfolio in the capital market. It is the important point remembers that According to the Portfolio

Theory, Efficient Portfolios are Fully Diversified and they must lie on the CML Line. Now, it is

also possible simply come up with the equation for the CML.

CML Equation: rP* = rRF + [(rM - rRF) / σM] σP

rRF= risk free rate of return

rM = expected rate of return for the market of all possible stock

σM = risk of the market

σP = risk of stock portfolio

The Expected Return on an Investment in a Common Share is not guaranteed or certain. The

Price and Dividend can vary so we can guess what the Possible future Returns (or Outcomes) might

be and assign probabilities to each. Uncertainty about Future Expected Return on Investment gives

rise to Probability Distribution of Possible Outcomes. This gives rise to a Spread of Possible Future

Returns which is a measure of the Risk or Uncertainty or Standard Deviation. We can apply this

100

Financial Management MGT201

concept to the single stock or a portfolio of a many stocks. When we talk about the expected return

on a single stock then we are saying that it is the combination of the dividend gain yield and the

capital gain yield. When we talk about the expected return for the portfolio then we consider

expected return for each stock in that portfolio and assign proportionate amount of weightage based

on the fraction of the investment in a particular stock compare to the total value of the portfolio.

Furthermore, the individual risk of every investment affects the risk of every other investment in the

portfolio! The Overall Portfolio Risk decreases as the number of investments increase up to the

point that the Company Specific or Unique Risk has been totally eliminated i.e. About 40

uncorrelated stocks. In this Range it is possible to Increase Return and Reduce Risk! After that,

the Portfolio is assumed to be Fully Diversified and any additional investment will only contribute

to the Market Risk which can not be eliminated.

Market Risk & Portfolio Theory:

We can measure that how market risk varies from one stock to another based on the Beta's. It is

mentioned that when you add newly stock to the fully diversified portfolio then the only contribution

this new stock is made to the risk of the existing portfolio is the market risk because we are considering

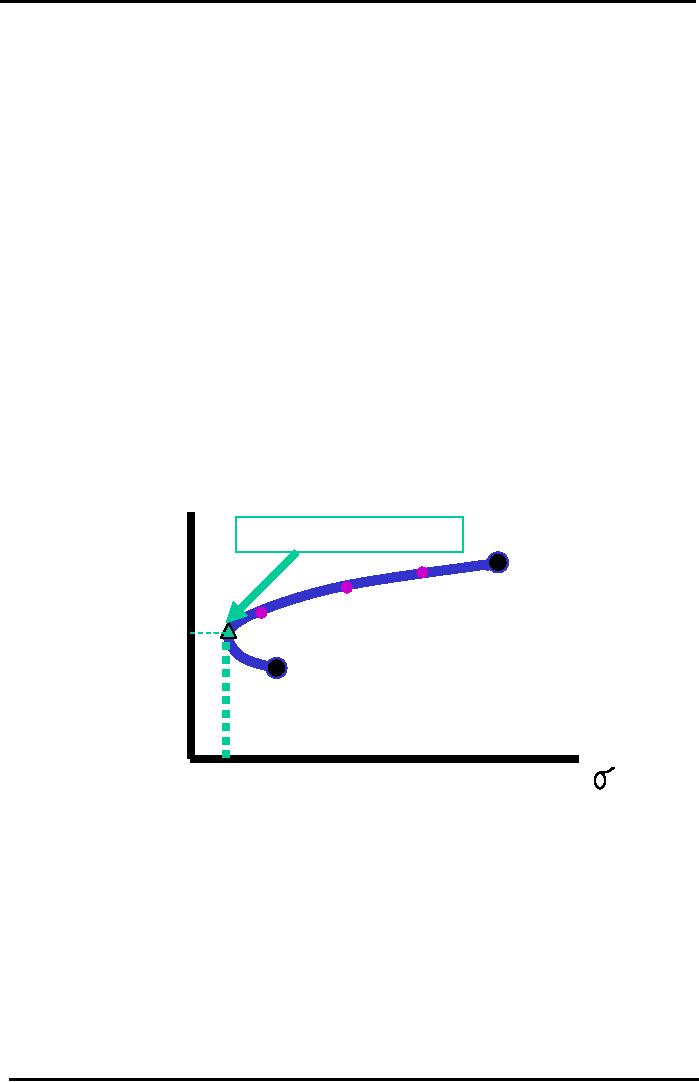
that company's unique risk has entirely wiped out by diversification. If the correlation between different

stocks is negative or Zero then risk and return profile graph takes on a hook shaped curve and this hook

shaped curve is important to understand because it means that it is possible for certain combinations of

the portfolio to both reduce risk and increase return.

Hook Shaped Curve

Negative Correlation Coefficient

Possible to Get Higher Return AND LOWER RISK

rP*

Point of Minimum Risk

Portfolio

20%

Return

Stock A

(100% A)

80%A

15%

50%A

13%

30%A

11.5%

15%A

10%

Stock B

(100% B)

3.4% 5%

20%

15%

Portfolio Risk

However, if the correlation coefficient is +ve then the risk return relationship is that of

continuous function which is continuously rising as return rises the risk also rises with it. It is the

fundamental concept in risk and return that the investor will not take on any additional risk unless

they compensated by additional return. It is important to under stand that when we are talking about

efficient capital markets and talking about the capital market line we are saying that efficient

portfolios in the market all lie on the capital market line. It means that if one investor is only

investing in the stock A and the other has a diversified portfolio of 40 stocks and now he is also

investing in Stock A then the amount of risk for both investors will be different the investor who is

only investing in stock A is taking on the Market risk of the stock as well as the company's risk

whereas the other investor is only taking on the market component risk for that stock. Rational

Investors with Diversified Portfolios expect to be compensated by extra return in exchange for

taking on Extra Market Risk.

You can NOT expect to receive extra return (or compensation) for taking on Company-Specific

Risk which Rational Investors have eliminated! The Efficient Market will only offer you a Return

101

Financial Management MGT201

(and a Share Price) which is the bare minimum acceptable to Rational Diversified Investors. This is

the Basis of the Capital Asset Pricing Model (CAPM).

Beta Concept & CAPM:

Beta:

It is a tendency of a Stock to move with the Market (or Portfolio of all Stocks in the Stock

Market).it is the building block of CAPM.

Stock Risk vs. Stock Beta:

Stock Risk:

It is a statistical spread of possible returns (or Volatility) for that Stock

Stock Beta:

It is a statistical spread of possible returns (or Volatility) for that Stock relative to the

market spread i.e. spread (or Volatility) of the fully diversified market portfolio or index.

Beta Coefficients of Individual Stocks are published in "Beta Books" by Stock Brokerages & Rating

Agencies

CAPM: Capital Asset Pricing Model.

It is developed by Professors Sharpe & Markowitz. He won Nobel Prize in 1990

Market Risk is the only risk that is relevant to a Rational Investor with a Diversified Portfolio of

Investments. The Company Specific (or Unique) Risk is Diversified Away! Market Risk is measured

in terms of the Standard Deviation (or Volatility) of the Market Portfolio or Index. Every Stock Market

develops an Index comprising of a weighted average of the highest-volume shares in that market. This

Index represents the relative strength of that Stock Exchange and is considered to be close to a Totally

Diversified Portfolio. In reality, no such Portfolio exists anywhere in the world. For example the

Karachi Stock Exchange has the KSE 100 Index.

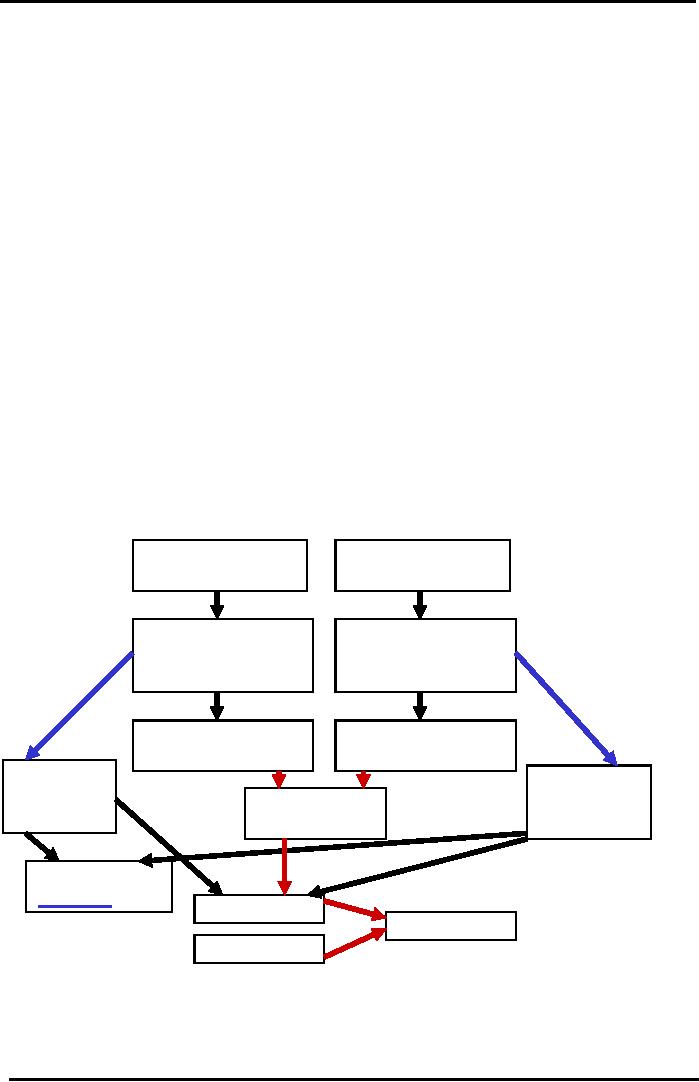
Return, Risk, and Beta

Stock B's Possible

Stock A's Possible

Future Returns

Stock B's Weighted

Stock A's Weighted

Average Return or

Expected Mean Return

Stock A's Risk or

Standard Deviation

Weightage of

Stock A in

Stock B in

Correlation

Portfolio

between 2 Stocks

Portfolio's

Expected Return

Portfolio Risk

Beta

Market Risk

102

Table of Contents: