RISK FOR A SINGLE STOCK INVESTMENT, PROBABILITY GRAPHS AND COEFFICIENT OF VARIATION

<< INTRODUCTION TO RISK, RISK AND RETURN FOR A SINGLE STOCK INVESTMENT:Diversifiable Risk, Diversification

2- STOCK PORTFOLIO THEORY, RISK AND EXPECTED RETURN:Diversification, Definition of Terms >>

Financial Management MGT201

Lesson 20

RISK FOR A SINGLE STOCK INVESTMENT, PROBABILITY GRAPHS AND CO-

EFFICIENT OF VARIATION

Learning Objectives:

After going through this lecture, you would be able to have an understanding of the following

topics

· Risk for Single Stock Investment

· Probability Graphs and Coefficient of variation

In this lecture, we will continue our discussion on risk and return. This is very important area of

financial management.

In previous lecture, we have mentioned an example for the investment in share and after one

year the share price has 3 possible outcomes. This uncertainty in future price of the share that leads to

the certain distribution in forecasted share price and this distribution is source of the uncertainty which

allow us to calculate risk.

3 Possible Outcomes Example Continued:

Measuring Stand Alone Risk for Single Stock Investment

Std Dev = δ =

√ ∑ (r i - < r i >) 2 p i.

(∑(r i - < r i >) 2 p i.)) 0.5.

= {[(40-10)2 (0.3)] + [(10-10)2 (0.4)] + [(-20-10)2 (0.3)] } 0.5 .

= {270 + 0 + 270} 0.5 = {Var} 0.5.

= {540} 0.5 = 23.24

How do we interpret this Result for Risk?

Standard Deviation Interpretation

What are the units of Standard Deviation?

For our example where Return is being estimated in % terms, the units of

Standard Deviation will also be %.

It tells us that if we assume a Normal Probability Distribution and symmetric about expected rate of

return, then we conclude that 68.26% of the time, the Actual Return will lie within -1 Standard

Deviation and +1 Standard Deviation of the Expected (or Mean) Return.

Expected (or Mean) Return = 10%

+/- 1 Standard Deviation = 10% +/- 23.24% which means from (10% - 23.24%) to (10% + 23.24%) i.e.

from -13.24% to 33.24%.

There is a 68.26% chance that the Actual Return on our Stock Investment after 1 year will be

somewhere between -13.24% and 33.24%. It is important thing to remember that in normal distribution

the area under the curve from -1 standard deviation to +1 standard deviation is 68.28%. So, we can be

sure that two thirds of the time the actual value for the return will be in between -13.68% and +33.24 %.

-13.24% is not a good sign as it indicates that we are making loss but remember that required rate of

return is 10%.

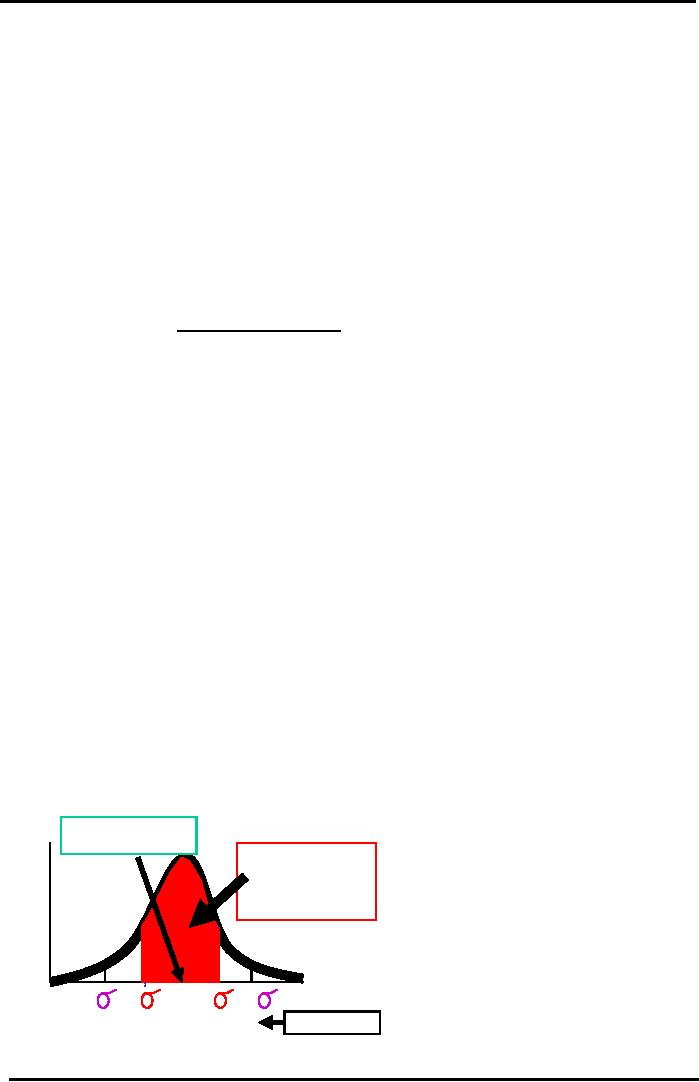
Graphical Standard Deviation

Expected (or Mean)

Return = <r> = 10%

+/- 1 Std Dev covers

68.26% of the Area

Prob

under the Normal

abili

Curve always

(p)

Return (r) %

-2

-1

-13.24%

+33.24%

Our Example

Financial Management MGT201

In the figure the probability is written on y-axis and the rate of return is mentioned on the x-axis.

It shows that higher the standard deviation the higher the risk.

Now, lets take a look another example in which we raw comparing three different investments

which we want to compare in terms of risk and return.

Example:

Comparison of 3 Investments in terms of Risk & Return. Which is the best Investment?

Risk (Std Dev)

Expected Return

Stock A

23.24%

10%

T-Bill/Bond B

10%

Project C

30%

T-Bill is Least Risky (lowest Std Dev =5%) and Project C has Highest Return (=30%).

Given 2 Investments with Identical Expected Return, choose the Investment with the Lower

Risk (or Spread or Volatility or Standard Deviation)

Given 2 Investments with Identical Risk, choose the Investment with the Higher Expected Return

If you compare first two investments, both have the same rate of return but the T-bills have less

risk. Clearly, T-Bill B is a better investment than Stock A because their Returns are identical (10%) but

the T-Bill is less risky (10%) than the Stock (23.24%).

But, which is better? T-Bill B or Project C? T-Bill B is Less Risky but Project C promises Higher

Return.

Now, we conceptually visualize these two types of investment

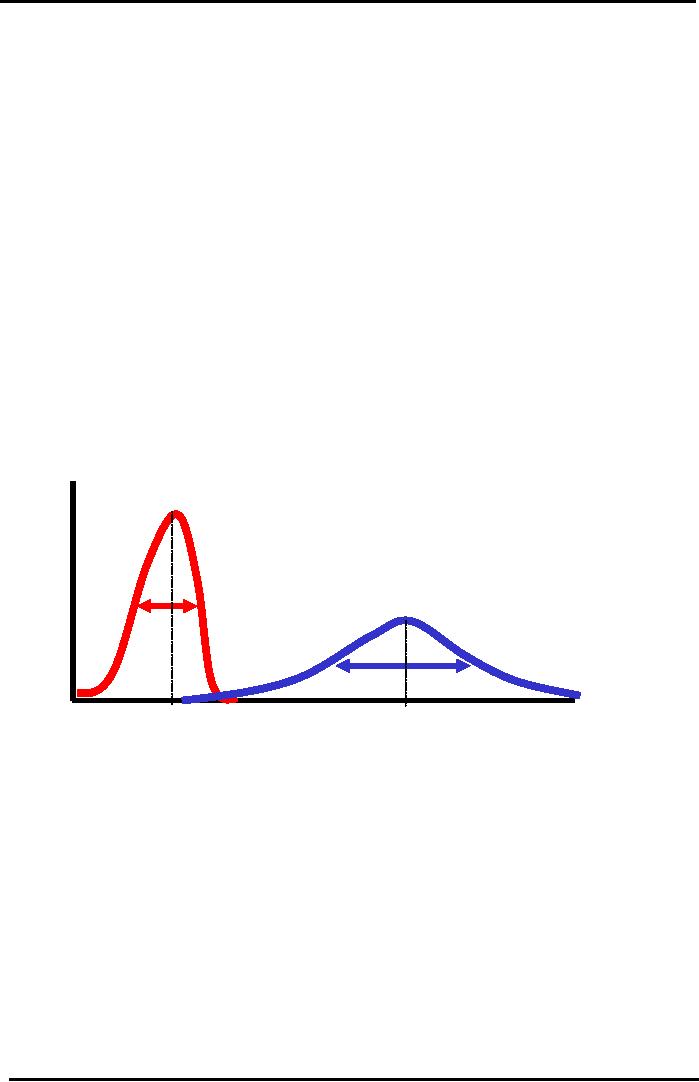
Combined Risk & Return

Graphical Comparison of Investments

T-Bill B: Low

Risk & Low

Proba

Return

bility

(p)

Project C: High

Risk B

Risk & High Return

Risk C

Exp Return C

Exp Return B

Rate of Return (r) %

In the figure, we are showing both investments on the same graph. Left hand shows the

probability distribution for the T- bills and on the right hand side shows the broader and shorter

probability graph for project C. How to visualize which project have higher expected rate of return.

Project C is on right hand side and therefore it has higher return as to project B.The other thing is that

project B form a probability distribution which have a sharp hill or spread of the curve is much narrower

as to project C. The standard deviation for project B is much narrower then the standard deviation for

project C .In project B has less risk whereas Project C has a higher expected rate return. We have to

look at risk and return simultaneously to answer that which option is better. We can derive the answer

with the help of the coefficient of variation

Comparison of Different Investments

Coefficient of Variation:

Coefficient of Variation (Risk per unit Return)

Financial Management MGT201

It is defined as the CV = Standard Deviation / Expected Return. Coefficient of Variation tells us

about the Risk per unit Return. The project which offers lowest per unit risk is the best investment. Now

we calculate the CV for both the projects.

Compare the CV's of the Projects:

CV T-bill = 5% / 10% = 0.5

CV Project C = 30% / 30% = 1.0

Choose the Project with the Lowest CV. Choose the T-Bill because it carries the lowest Risk per unit

Return

Risk Aversion Assumption

Most Investors are psychologically Risk Averse. If two investments offer the same Expected

Return, most Investors would choose the one with the lower Risk (or Standard Deviation or Spread

or Volatility). In other words, most Investors are not major gamblers. Note that gamblers would

choose Project C which appeals to investor greed by offering an upside return of 30%+10% = 40% !

Consequences on Share Price: The Higher the Risk of a Share, the Higher its Rate of Return and the

Lower its Market Price.

Table of Contents: