SOME SPECIAL AREAS OF CAPITAL BUDGETING:SOME SPECIAL AREAS OF CAPITAL BUDGETING, SOME SPECIAL AREAS OF CAPITAL BUDGETING

<< PROJECT CASH FLOWS, PROJECT TIMING, COMPARING PROJECTS, AND MODIFIED INTERNAL RATE OF RETURN (MIRR)

CAPITAL RATIONING AND INTERPRETATION OF IRR AND NPV WITH LIMITED CAPITAL.:Types of Problems in Capital Rationing >>

Financial Management MGT201

Lesson 11

SOME SPECIAL AREAS OF CAPITAL BUDGETING

Learning Objectives:

In this lecture, we will discuss some special areas of capital budgeting in which the calculation

of NPV & IRR is a bit more difficult. These concepts will be explained to you with help of numerical

example.

As it is mentioned in the previous lectures that we are studying the area of capital budgeting as

it relates to projects, which means investments in real assets (land, property etc.) The major difficulty in

the NPV calculation is your ability to forecast the cash flows. Therefore, it is necessary that one should

spent time on this so that the cash flow forecast is accurate.

We, have a simple formula to calculate the cash flows. The way we define the net Incremental

after tax cash flows for the purposes of this course is

Net After-tax Cash Flows = Net Operating Income + Depreciation + Tax Savings from Depreciation +

Net Working Capital required for this project + Other Cash Flows

The things we left out from the formula given above are certain incidental cash flows (Include

Opportunity Costs and Externalities but Exclude Sunken Costs.)

Two Major Criteria of Capital Budgeting:

1. Net Present Value (NPV)

2. Internal Rate of Return (IRR)

a. Combined View: NPV Profile (NPV vs i Graph)

The NPV is the most important because it has a direct link with shareholders wealth maximization.

Let us discuss in detail about the difficulties faced in NPV & IRR with the help of certain

numerical examples and explanations.

First, we would discuss the case of Multiple IRRs.

Multiple IRR:

In this case, you have a project with certain cash flows that are not normal and when

you try to calculate IRR you obtain more than one IRR answer. This is the case where you have more

than one sign change taking place in your cash flow diagram. Sign change means that you have two

adjacent arrows one of them is downward pointing & the other one is upward pointing. In general, our

cash flow diagram starts with down ward pointing arrow (Investment) and it is followed with series of

upward pointing arrows (net incoming cash) during the life of project. However, during the life of

project if you have any net cash outflow or downward pointing arrow then that would be second sign

change and you can expect to have multiple answer for IRR.

In this particular case, calculating the NPV and setting it equal to zero to calculate IRR will give

you two answers & both of them would be wrong.

The alternative is to use Modified IRR or MIRR approach.

MIRR Approach:

The logic behind MIRR is that instead of looking at net cash flows you look at cash inflows and

outflows separately for each point in time. Discount all the Outflows during the life to the present and

Compound all the Inflows to the termination date. Assume reinvestment at a Cost of Capital or Discount

Factor (or Required Return) such as the risk free interest rate.

The MIRR represents the discount rate, which will equate the Future Value of cash inflows to

Present Value of cash outflows.

Formula:

(1+MIRR) n = CF in * (1+k) n-t

CF out /(1+k) t

Modified Internal Rate of Return (MIRR) would provide us with an answer, which is entirely different

from our previous IRR calculations

Example:

A project with the following cash flows: Initial Investment = -Rs100, Year 1 = +Rs500, Year 2 = -

Rs500

If we use standard NPV equation to calculate the IRR

IRR Equation: NPV = 0 = -100 + 500/ (1+IRR) - 500/ (1+IRR) 2

You would come up with 2 answers

Financial Management MGT201

IRR = 38% and 260%

Both of these answers are incorrect. Therefore, we will use the modified IRR approach to calculate the

actual IRR for this project.

MIRR Approach (Assume Cost of Capital k = 10%):

(1+MIRR) n =

CF in * (1+k) n-t

CF out / (1+k) t

We use 1.1 as compound factor because we assume "i"=10% = Risk free rate return. Here`t' refers to

the time in which a particular cash flow occurs, while `n' is the total life span of the project.

(1+MIRR) 2 = 500 * (1+0.1)2-1

(100 / 1.1) + (500 / (1+0.1)2

(1+MIRR) 2 = 550 / 513 = 1.07

MIRR = 0.0344 = 3.44%

This answer is entirely different from the previous answers that we got from calculating the IRR.

However, MIRR gives you the best possible answer and the most realistic too.

Now, let us talk about the case of comparing projects with different lives.

NPV of Projects with Different Lives:

Suppose that you have two projects having different life spans. It is not entirely accurate to

calculate NPV's in simple manner and to compare them and pick the project with higher NPV. Because

you are comparing a certain project that is generating cash flows for a short period of time with another

project that is yielding cash flows over a longer time. We use following two approaches to rank these

kinds of projects.

Common Life Approach:

In this approach, the idea is quite simple. You need to bring all the projects to the same

length in time. In other words, you are required to convert all the projects to the identical life

span. You can do that by finding least common multiple for common life. For example, if you

are comparing two projects one has life of 4 years and the other, which has a life of 5 years, the

least common multiple is 20 years. Sketch out the cash flow diagram and repeat the cash flow

for each of the project such that they fit in exact number of time in 20 years. In case of project

with a life of 4 years, you can replicate the cash flows 5 times in a period of 20 years. . In case

of project with a life of 5 years, you can replicate the cash flows 4 times in a period of 20 years.

Compute the NPV of each project over the common life and choose the project with the highest

NPV.

Equivalent Annual ANNUITY (EAA) Approach:

In this case, our logic is to find out that for a particular project of limited life giving you

the certain net present value calculated in a simple way, what kind of yearly annuity gives the same

NPV. You can then compare annual annuity of each project and choose the highest. You are comparing

cash flow of two projects both of which are taking place in a period of one year only. You can also

convert the cash flows of the project to the perpetuity, which is infinite, and then you can compare the

NPV's like of different projects. That is also correct since life spans are identically infinite.

Example:

We have 2 Projects with following Cash Flows:

Project A: Io= - Rs100, Yr 1 = +Rs200

Project B: Io= - Rs200, Yr1= +Rs200, Yr2= +Rs200

Simple NPV Computation (assuming i=10%):

NPV Project A = -100 + 200/1.1 = +Rs 82

NPV Project B = -200 + 200/1.1 + 200/ (1.1)2 = +Rs 147

Conclusion from Simple (or Normal) NPV Calculation is that Project B is better. It is incorrect because

here we are comparing apples to the oranges since the project lives are different!

Common Life Approach:

Common Life Span=Least common multiple = 2 Years (because this is the shortest cycle in which both

project lives can exactly be replicated back to back).

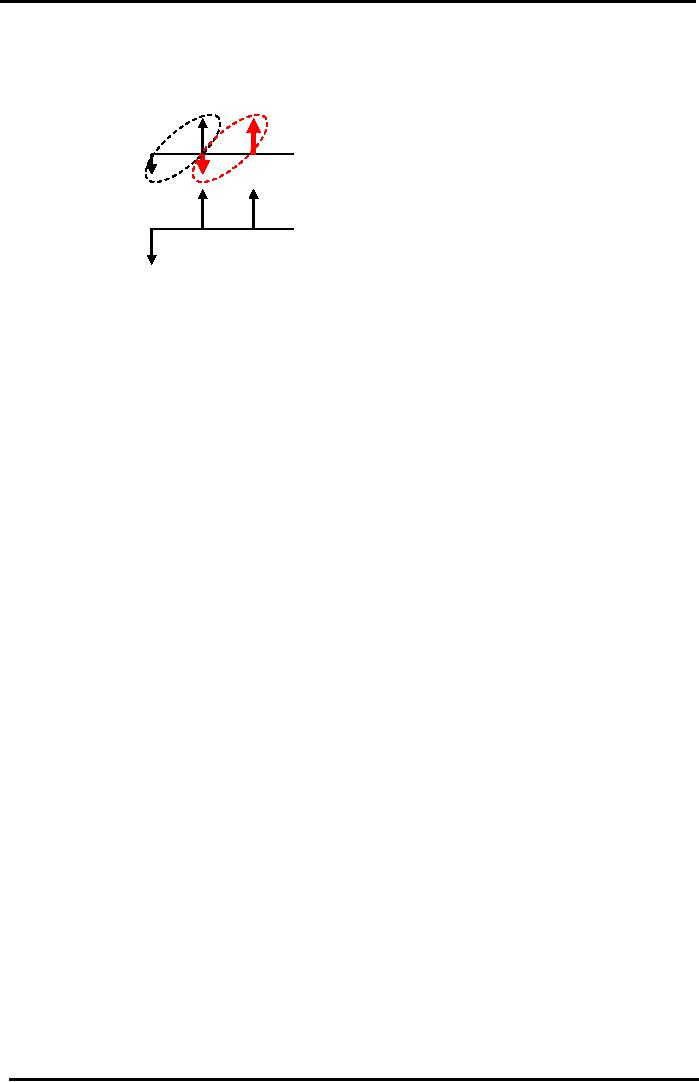
Financial Management MGT201

Project A:

+200

Yr 0

Yr 1

Yr 2

-100

+200

Project B:

Yr 0

Yr 1

Yr 2

-200

In this Cash Flow Pattern of A is repeated exactly 2 times to cover the life of the longer Project

B. The project A's outflow 100 & inflow of 200 then we replicate it with down ward pointing arrow

with 100 and upward pointing arrow with 200 amount in the 2nd year. Project B remains unchanged

Common Life (C.L.) NPV's:

Project A C.L. NPV = -100 + [(200-100)/1.1] + 200/ (1.1)2 = +Rs 156

Project B C.L. NPV = Same as before = +Rs 147

Now our conclusion has changed! After doing the Common Life NPV, Project A looks better. The

Simple NPV of Project A was + Rs 82 but after increasing its life to match Project B's, the NPV of

Project A increased. It is the correct answer. Also, note that how the NPV of A increased from 82 to 156

(almost double) because you double the life of the project.

Now we solve this problem with Equivalent Annual Annuity Approach

Equivalent Annual Annuity Approach:

In this we are explaining that how we can achieve same NPV value from an annuity stream.

Here, we are doing a back calculation that we knew the NPV's but which annuity stream they are

representing with in the life span of the project. Then we compare the annual annuity of both projects.

The life span remains same

Example:

Start with the Simple (or Normal) NPV's calculated earlier (at i = 10%):

Project A Simple NPV = + Rs 82

Project B Simple NPV = + Rs 147

To find EAA

Multiply the Simple NPV of each project by the EAA Factor

EAA FACTOR = (1+ i) n / [(1+i) n -1] where n = life of project & i=discount rate

Project A's EAA Factor = 1.1 / (1.1-1) = 11

Project B's EAA Factor = 1.12 / (1.12-1) = 5.76

EAA for each project

Project A's EAA = Simple NPV * EAA Factor = 82*11= + Rs 902

Project B's EAA = 147*5.76 = + Rs 847

Conclusion: Project A is better. Same conclusion as Common Life Approach but of course the

numbers for EAA and NPV are different.

Practical view:

Companies and individuals running different types of businesses have to make the choice of the asset

according to the life span of the project. For instance, a tailor shop owner would have to decide whether

to invest in a sewing machine that has a useful life of ten years or to invest in another machine with a

Financial Management MGT201

useful life of three years. These decisions are important since they involve major cash outflows of the

business. There are advantages & disadvantages associated with different life span.

Different Lives & Budget Constraint:

Companies and individuals running different types of businesses have to make the choice of the

asset according to the life span of the project.

Advantages of asset with a long life:

The advantage of a longer asset life is that the cash flows from the project become more

predictable, since there are lesser cash outflows occurring during the life of the project.

Disadvantage of asset with very long life:

It does not give you the opportunity (or option) to extract full value of asset and replace the

equipment quickly in order to keep pace with technology, better quality, and lower costs.

Advantages of asset with short life

The advantage of a short life asset is that the investor, by making reinvestment in the asset of a

superior quality, lowers down the costs and updates the project to the new technological requirements.

Disadvantage of assets with very short life:

The disadvantage is that the money will have to be reinvested in some other project with an

uncertain NPV and return so it is risky. If a good project is not available, the money will earn only a

minimal return at the risk free interest rate.

While exercising the option of different project timing, the projects can be compared by applying

Common Life and EAA Techniques to quantitatively.

Budget Constraint

We have been addressing the issue of capital budgeting with very idealistic assumptions. In

practical life, individuals and companies have a limited amount of money and limited human resources

in terms of either skill or numbers. It can be argued that the firm can also meet their requirements by

borrowing. IN real life, managers may avoid borrowing to limit their risk exposure. This prevents them

from undertaking projects with high positive NPVs that would have added to the firm's value and

maximized shareholder wealth!

Table of Contents: