BREAKEVEN ANALYSIS â€“ CHARTS AND GRAPHS:Usefulness of charts

<< BREAK EVEN ANALYSIS â€“ MARGIN OF SAFETY:Margin of Safety (MOS), Using Budget profit

WHAT IS A BUDGET?:Budgetary control, Making a Forecast, Preparing budgets >>

Cost & Management Accounting (MGT-402)

LESSON# 32

BREAKEVEN ANALYSIS CHARTS AND GRAPHS

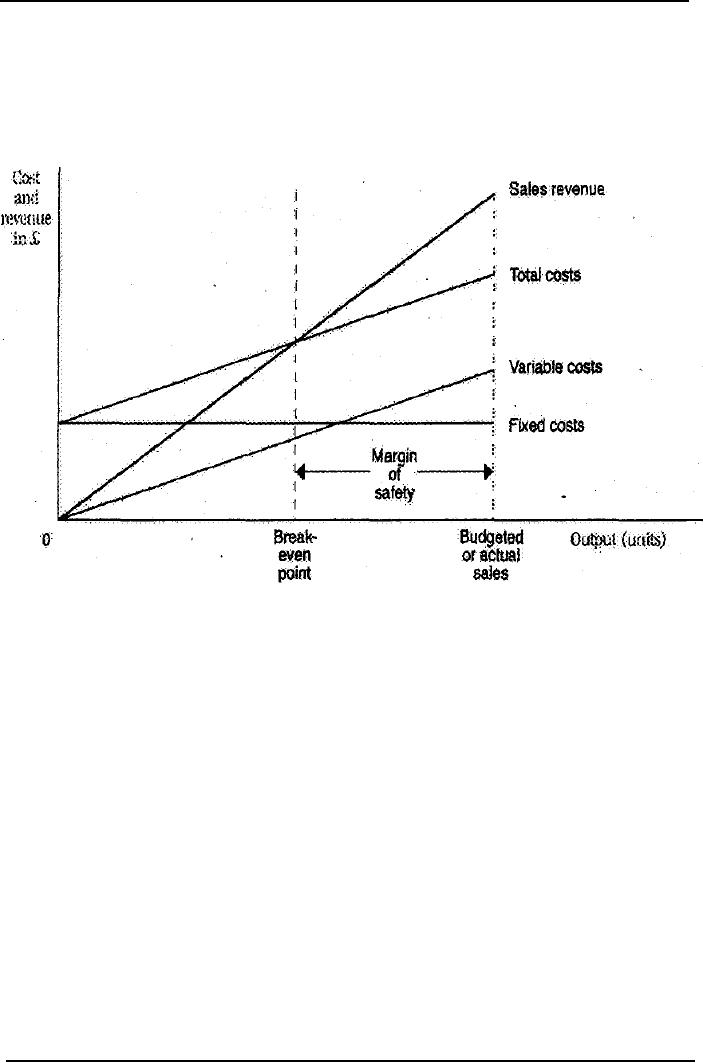
The conventional break-even chart

The conventional break-even chart plots total costs and total revenues at different output levels

and shows the activity level at which break-even is achieved.

Conventional break-even chart

The chart or graph is constructed as follows:

· Plot fixed costs, as a straight line parallel to the horizontal axis

· Plot sales revenue and variable costs from the origin

· Total costs represent fixed plus variable costs.

The point at which the sales revenue and total cost lines intersect indicates the breakeven level of

output. The amount of profit or loss at any given output can be read off the chart.

By multiplying the sales volume by the unit price at the break-even point the level of revenue

needed to break even can be determined.

The chart is normally drawn up to the budgeted sales volume.

The difference between the budgeted sales volume and break-even sales volume is referred to as

the margin of safety.

Usefulness of charts

The conventional form of break-even charts was described above. Many variations of such charts

exist to illustrate the main relationships of costs, volume and profit.

Unclear or complex charts should, however, be avoided, as a chart which is not easily understood

defeats its own object.

Generally, break-even charts are most useful for the following purposes:

· comparing products, time periods or actual outcomes versus planned outcomes

· showing the effect of changes in circumstances or to plans

· giving a broad picture of events,

195

Cost & Management Accounting (MGT-402)

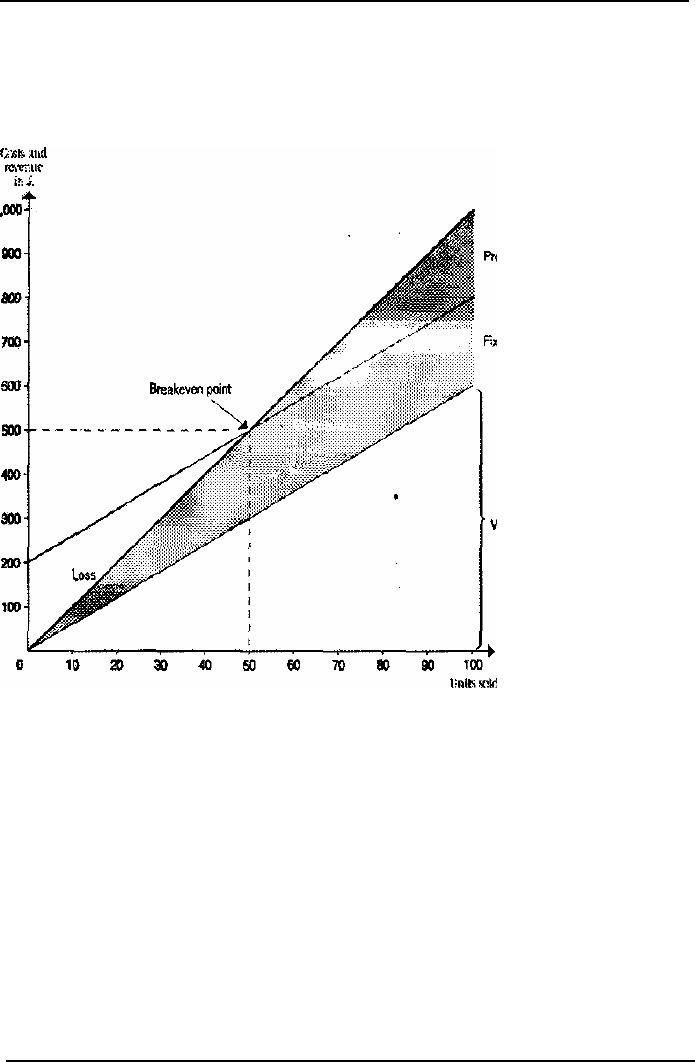
Contribution break-even charts

A contribution break-even chart is constructed with the variable costs at the foot of the diagram

and the fixed costs shown above the variable cost line.

The total cost line will be in the same position as in the break-even chart illustrated above; but by

using the revised layout it is possible to read off the figures of contribution at various volume

levels, as shown in the following diagram.

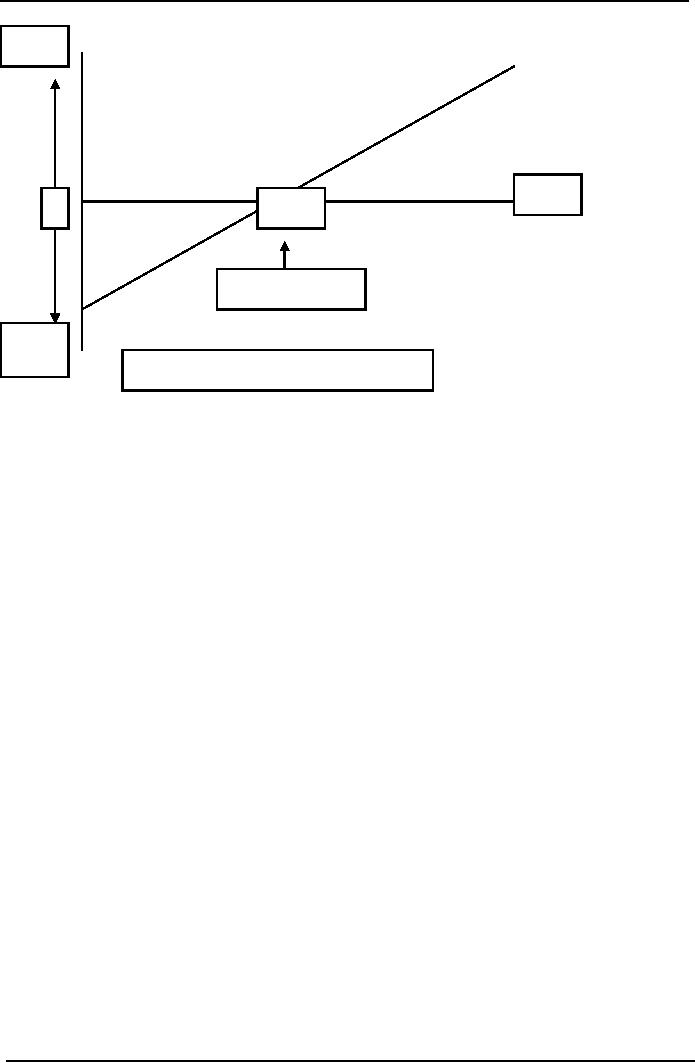
Profit-volume chart

A profit-volume chart is a graph which simply depicts the net profit and loss at any given level of

activity.

196

Cost & Management Accounting (MGT-402)

Profit

Sales

500

Breakeven Point

Loss

1,000

Loss = Fixed cost at zero sales activity

From the above chart the amount of net profit or loss can be read off for any given level of sales

activity, unlike a break-even chart which shows both costs and revenues over a given range of

activity but does not highlight directly the amounts of profits or losses at the various levels.

The points to note in the construction of a profit-volume chart are as follows:

The horizontal axis represents sales (in units or sales value, as appropriate). This is the same as

for a break-even chart.

The vertical axis shows net profit above the horizontal sales axis and net loss below.

When sales are zero, the net loss equals the fixed costs and one extreme of the 'profit-volume'

line is determined. Therefore this is one-point on the graph or chart.

If variable cost per unit and fixed costs in total are both constant throughout the relevant range

of activity under consideration, the profit-volume chart is, depicted by a straight line (as

illustrated above). Therefore, to draw that line it is only necessary to know the profit (or loss)

at one level of sales. The 'profit-volume ' line is then drawn between this point and the one for

zero sales, extended as necessary.

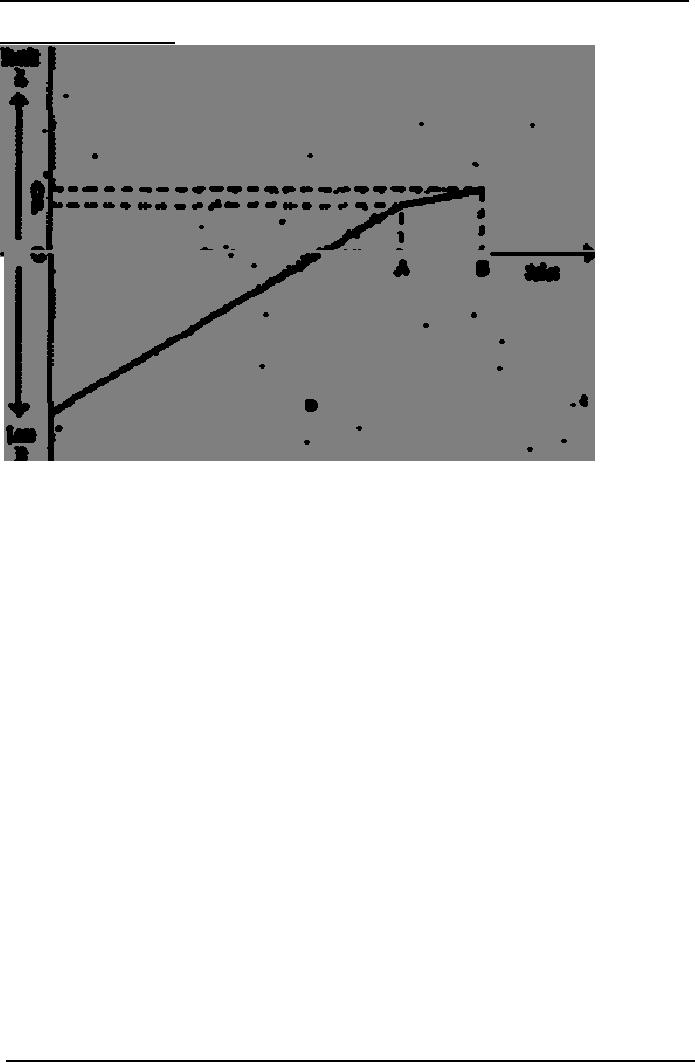
If there are changes in the variable cost per unit or total fixed costs at various activities, it

would be necessary to calculate the profit (or loss) at each point where the cost structure

changes and to plot these on the chart. The 'profit-volume' line will then be a series of straight

lines joining these points together, as shown in the simple illustration below.

197

Cost & Management Accounting (MGT-402)

Profit-volume chart (2)

This illustration depicts the situation where the variable cost per unit increases after a certain level

of activity (OA), e.g. because of overtime premiums that are incurred when production (and sales)

exceed a particular level.

Points to note:

· The profit (OP) at sales level OA would be determined and plotted.

· Similarly the profit (OQ) at sales level of OB would be determined and plotted.

· The loss at zero sales activity (= fixed costs) can be plotted.

· The "profit-volume' line is then drawn by joining these points, as illustrated.

As long as we make the assumptions that contribution per unit is constant, and fixed costs do not

change, we can draw straight-line graphs to show profit or costs and revenues at all possible

activity levels.

MULTIPLE CHOICE QUESTIONS

1. If contribution margin is positive?

(a) Profit will occur.

(b) Both a profit and loss are possible.

(d) A loss will occur if the contribution margin is greater than fixed expenses.

2. At the breakeven point:

(a) Profit is Rs. 0.

(b) . Fixed Cost + Variable Cost = Safes

(d) All of the above

198

Cost & Management Accounting (MGT-402)

A completed CVP graph will show that profit or loss at any level of sales is measured by:

(a)

A vertical line between the fixed cost line and the x axis.

(b)

A horizontal line between the revenue line and the y axis.

(c)

A vertical line between the total revenue line and the total expenses line.

(d)

A horizontal line between the total revenue line and the total expenses line.

Contribution margin ratio is:

(a)

Total Contribution Margin / Sales.

(b)

Sales / Contribution Margin per unit,

(c)

Fixed cost / Contribution margin per unit.

(d)

Sales / Variable costs.

5. The impact on net operating income of any given dollar change in total sales can be computed

by applying which ratio to the dollar change?

(a) Profit margin.

(b) Variable cost ratio.

(d) Ratio of Variable to Fixed Expenses.

6. The Hino Corporation has a breakeven point when sales are Rs. 160,000 and variable costs at

that level of sales are Rs. 100,000. How much would contribution margin increase or decrease, if

variable expenses dropped by Rs. 20,000?

(a) 37.5%.

(b) 60%.

(d) 26%

Which of the following represents the CVP equation?

(a)

Sales = Contribution margin + Fixed expenses + Profits

(b)

Sales = Contribution margin ratio + Fixed expenses + Profits

(c)

Sales = Variable expenses + Fixed expenses + Profits

(d)

Sales = Variable expenses - Fixed expenses + Profits

Margin of Safety is a term best described as the excess of:

(a)

Contribution margin over fixed expenses.

(b)

Total expenses over the breakeven point.

(c)

Sales over the breakeven point.

(d)

Sales over total costs.

Point out which of the following statements are TRUE/FALSE

Cost-volume-profit (CVP) analysis summarizes the effects of change on an organization's

volume of activity on its costs, revenue, and profit.

2. The break-even point is the volume of activity where an organization's revenues and expenses

are equal,

Total contribution margin can be calculated by subtracting total fixed costs from total

revenues.

4. Contribution margin / Sales price per unit = Contribution margin ratio.

5. The sales price of a single unit minus the unit's variable expenses is called the unit contribution

margin-

199

Cost & Management Accounting (MGT-402)

6. The contribution-margin ratio of a firm is determined by dividing the per unit contribution

margin by the per unit sales price.

7. The safety margin of an enterprise is the difference between the budgeted sales revenue and

the break-even sales revenue-

8. A company's break-even sales revenues are Rs, 400,000, and its contribution margin is 40%. If

fixed costs increase by Rs. 24,000, breakeven sales will increase to Rs. 440,000.

9. If the total contribution margin at break-even sales is Rs, 45,000, then the fixed costs must

also be Rs. 45,000,

10. If a company sells 50 units of A at Rs. 8 contribution margin and 200 units of B at a Rs. 6

contribution margin, the weighted-average contribution margin is Rs. 7.00.

200

Table of Contents: