 |
Chapter
One
LIGHT
THEORY
The
Spectrum, Human Eye
Response
Light is a
form of energy. Virtually
all the energy you
use on a daily basis began
as sunlight energy
striking
the earth. Plants capture
and store some the sun's energy and
convert it into
chemical
energy.
Later, you use that
energy as food or fuel. The
rest of the sun's energy heats
the earth's
surface,
air and oceans.
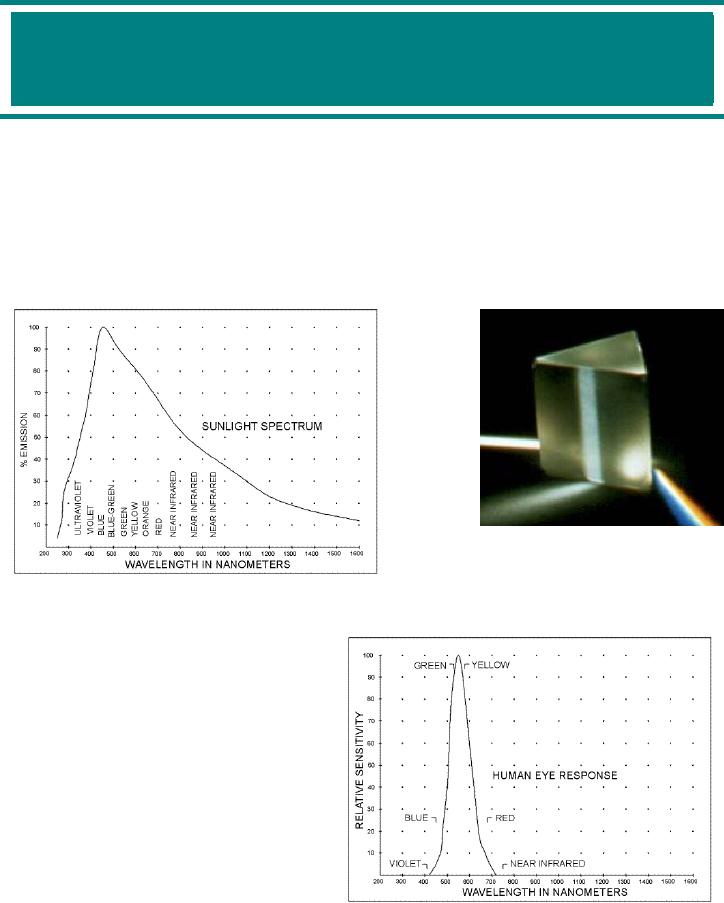
White
light disperses
color
spectrum through a
prism
Figure
1a
With
the aid of a glass prism you
can
demonstrate
that the white light
coming
from
the sun is actually made up
of many
different
colors as shown in Figure
1a.
Some
of the light falls into
the visible
portion
of
the
spectrum
while
wavelengths,
such as the infrared
and
ultraviolet
rays, remain invisible.
The
human
eye responds to light according
to
the
curve shown on Figure
1b.
The
spectrum
that lies just outside
the human
eye
red sensitivity limit is called
"near
infrared"
or simply IR. It is this portion
of
the
spectrum that is used by
much of
today's
light-beam
communications
Figure
1b
systems.
Page
10
of 68
Optical
Through-the-Air Communications Handbook
-David A. Johnson, PE
As
can be seen from Figure
1a, sunlight
is a very powerful source for
this band of light, so
are
standard
incandescent lamps and light from
camera photoflash sources. However,
many other man-
made
light emitters, such as
fluorescent lamps and the
yellow or blue/white street lamps,
emit very
little
infrared light.
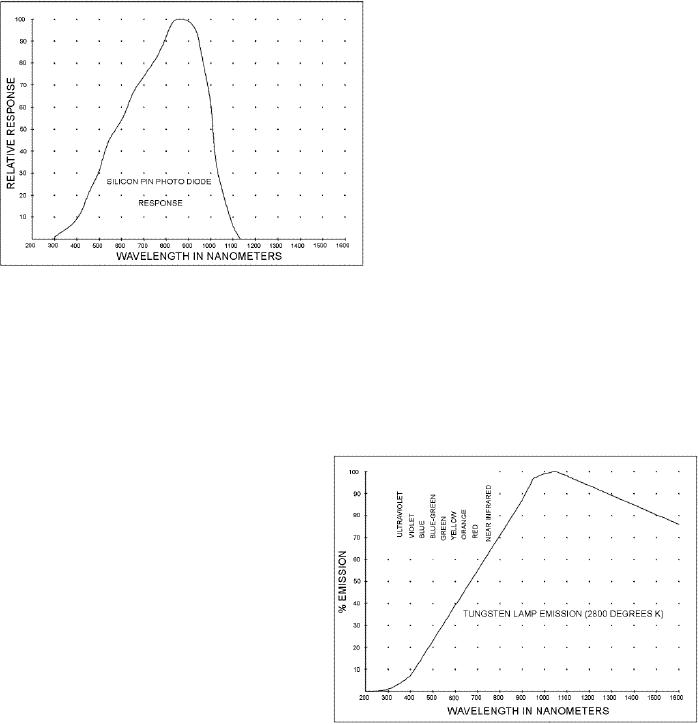
Silicon
Detector Response
Just
as our eyes are more
sensitive to
certain
wavelengths so are some
electronic
light
detectors. As shown in Figure
1c a
typical
silicon light detector has a
response
curve
that ranges from the
longer mid-
infrared
wavelengths, through the
visible
portion
of the spectrum and into
the
shorter
and also invisible ultraviolet
wavelengths.
The most notable feature
of
the
silicon detector's curve is its
peak
sensitivity
at about 900 nanometers.
Also
note
that at 600 nanometers, visible
red,
the
silicon detector response is
about one
half
that of its peak. It should
therefore be
clear
that any light source with a
900
Figure
1c
nanometer
wavelength would have
the
best
chance of being detected by the
silicon detector. Fortunately, as we
shall see in the section
on
light
emitters, many of today's
infrared light emitting
diodes (LEDs) do indeed emit
light at or near
this
900nm peak.
Units
of Light
As
shown in Figure
1d a
standard
tungsten
incandescent light bulb emits
a
very
broad spectrum of light. If you
took
all
the
light
wavelengths
into
consideration,
including all those that
were
invisible
to the human eye, the
light bulb's
electrical
power to light power
conversion
efficiency
would
approach
100%.
However,
much of the light emitted
from
such
a source takes the form of
long
infrared
heat wavelengths. Although
still
considered
light, heat wavelengths
fall
well
outside the response curve
of both our
human
eye and a silicon detector. If
you
only
considered the visible portion of
the
Figure
1d
spectrum,
the light bulb's efficiency
would
only
be about 10%. But, to a
detector that was sensitive to heat
wavelengths, the bulb's
efficiency
would
appear to be closer to 90%.
This takes us to one of the
most confusing areas of science.
How
do
you define the brightness or
intensity of a light
source?
Page
11
of 68
Optical
Through-the-Air Communications Handbook
-David A. Johnson, PE
It
isn't enough to say that a standard 100
watt bulb emits more
light than a tiny 1 watt
bulb. Sure, if
you
set a big 100 watt bulb
next to a small 1 watt
flashlight bulb, the 100
watt bulb would appear
to
emit
more light. But there
are many factors to consider
when defining the brightness
of a light
source.
Some factors refer to the
nature of the emitted light
and others to the nature of
the detector
being
used to measure the
light.
For
some light emitting devices,
such as a standard tungsten incandescent
light bulb, the light
is
projected
outward in all directions
(omni-directional). When visually
compared to a bare 1 watt
bulb,
the light emitted from a
bare 100 watt bulb would
always appear brighter.
However, if you
were
to position the tiny 1 watt
bulb in front of a mirror,
like a flashlight reflector,
the light
emerging
from the 1 watt light
assembly would appear much
brighter than the bare 100
watt, if
viewed
at a distance of perhaps 100 feet. So,
the way the light is
projected outward from the
source
can
influence the apparent brightness of
the source. An extreme example of a
highly directional
light
source is a laser. Some lasers, including
many common visible red laser
pointers, are so
directional
that the light beams
launched spread out very
little. The bright spot of
light emitted
might
remain small even after
traveling several hundred
feet.
The
preferential treatment that a
detector gives to some light
wavelengths, over others, can
also
make
some sources appear to be
brighter than others. As an
example, suppose you used a
silicon
light
detector and compared the light
from a 100 watt black-light
lamp that emits
invisible
ultraviolet
light, with a 100 watt
tungsten bulb. At a distance of a few
feet, the silicon
detector
would
indicate a sizable amount of
light being emitted from
the light bulb but
would detect very
little
from the black-light source,
even though the ultraviolet
light could cause skin
burns within
minutes.
So which is brighter?
In
order to define how much
light a source emits you
first need to specify what
wavelengths you
wish
to be considered. You must also assign a
certain value to each of the
considered wavelengths,
based
on the detector being used.
In addition, since many light
sources launch light in all
directions
you
must also define the
geometry of how the light is
to be measured. Perhaps you only
want to
consider
the amount of light that can
be detected at some distance away.
The wavelengths you
may
want
to consider will depend on the
instrument used to make the measurements.
If the instrument is
the
human eye then you need to
consider the visible
wavelengths and you will need to
weigh each
of
the wavelengths according to
the human eye sensitivity
curve. If the instrument
were a silicon
detector,
then you would use
its response curve.
When
doing research on light, you
will come across many different
units being used by
various
light
manufacturers. All the units
are trying to describe how
much light their devices
emit. You will
see
units such as candle power,
foot candles, candelas, foot lamberts,
lux, lumens and my
favorite:
watts
per steradian. Some units refer to
the energy of the light
source and others to the power.
Many
units
take only the human eye
sensitivity into account.
The light units can be even
more confusing
when
you consider that some
light sources, such as a common
light bulb, launch light in
all
directions
while others, such as a
laser, concentrate the light
into narrow beams. Rather
than
confuse
you even more by going
into a long discussion of
what the various units mean,
I'm going to
try
to simplify the problem.
Let's just assume that
each light source has a
distinctive emission
spectrum
and a certain emission geometry. You will
have to treat each light
source differently,
according
to how it is used with a
specific communications
system.
Page
12
of 68
Optical
Through-the-Air Communications Handbook
-David A. Johnson, PE
In
optical communications you
only need to consider the
light that is sent in the
direction of the
detector.
You also only need to consider
the light that falls
within the response curve of
the detector
you
use. You should regard all
the rest of the light as
lost and useless. Since all
the light sources
discussed
in this book rely on
electricity to produce light,
each source will have an
approximate
electrical
power (watts) to optical
power (watts) conversion
efficiency, as seen by a silicon
detector.
You
can use the approximate
power efficiency and the
known geometry of the
emitted light to
calculate
how much light will be
emitted, sent in the direction of
the light detector and
actually
collected.
Various sections of this book will
give you some examples of
such calculations.
Light
Power and Intensity
The
scientific unit for power is
the "watt". Since the
intensity of a light source can also be
described
as
light power, the watt is
perhaps the best unit to
use to define light
intensity. However,
power
should
not be confused with energy.
Energy, is defined as power
multiplied by time. The
longer a
light
source remains turned on,
the more energy it
transmits. But, all of the
light detectors discussed
in
this book are energy
independent. They convert
light power into electrical
power in much the
same
way as a light source might
convert electrical power
into light power. The
conversion is
independent
of time. This is a very
important concept and is paramount to
some of the circuits
used
for
communications. To help illustrate
how this effects light
detection, imagine two light
sources.
Let
us say that one source emits one watt of
light for one second while
the other launches a
million
watts
for only one millionth of a second. In
both cases the same
amount of light energy is
launched.
However,
because light detectors are
sensitive to light power,
the shorter light pulse will
appear to
be
one million times brighter and will
therefore be easier to detect. This
peak power
sensitivity
concept
of light processing is a very important
concept and is often neglected in
many optical
communications
systems published in various
magazines.
Miscellaneous
Stuff
Independent
on how long the light
remains on. The watt is
more convenient to use since
light
detectors,
used to convert the light
energy into electrical
energy, produce an electrical
current
proportional
to the light power, not
its energy. Detectors often
have conversion factors
listed in
amps
per watt of light shining on
the detector. Remember,
energy is power multiplied by
time.
Page
13
of 68
Optical
Through-the-Air Communications Handbook
-David A. Johnson,
PE
Table of Contents:
- LIGHT THEORY:The Spectrum, Human Eye Response, Silicon Detector Response
- LIGHT DETECTORS:The Silicon PIN Photodiode, Active Area, Response Time
- LIGHT EMITTERS:Light Emitting Diodes (LEDs), Solid State Semiconductor Lasers
- LIGHT SYSTEMS CONFIGURATIONS:Opposed Configuration, Diffuse Reflective Configuration
- LIGHT PROCESSING THEORY:Lenses as Antennas, Light Collimators and Collectors
- OPTICAL RECEIVER CIRCUITS:Current to Voltage Converter Circuits, Post Signal Amplifiers
- OPTICAL TRANSMITTER CIRCUITS:Audio Amplifier with Filters, Pulsed Light Emitters