 |
Handling uncertainty with fuzzy systems |
| << Expert Systems |
| Introduction to learning >> |

Artificial
Intelligence (CS607)
6 Handling uncertainty with fuzzy
systems
6.1
Introduction
Ours is a
vague world. We humans, talk
in terms of `maybe', `perhaps',
things
which
cannot be defined with cent
percent authority. But on
the other hand,
conventional
computer programs cannot
understand natural language
as
computers
cannot work with vague
concepts. Statements such
as: "Umar is tall",
are
difficult for computers to
translate into definite
rules. On the other
hand,
"Umar's
height is 162 cm", doesn't
explicitly state whether
Umar is tall or
short.
We're
driving in a car, and we see an
old house. We can easily
classify it as an
old
house. But what exactly is
an old house? Is a 15 years
old house, an old
house? Is 40
years old house an old
house? Where is the dividing
line between
the
old and the new houses? If
we agree that a 40 years old
house is an old
house,
then how is it possible that a
house is considered new when
it is 39 years,
11 months
and 30 days old only. And
one day later it has become
old all of a
sudden?
That would be a bizarre
world, had it been like that
for us in all
scenarios of
life.
Similarly
human beings form vague
groups of things such as
`short men', `warm
days',
`high pressure'. These are
all groups which don't
appear to have a well
defined
boundary but yet humans
communicate with each other
using these
terminologies.
6.2
Classical sets
A classical
set is a container, which
wholly includes or wholly
excludes any given
element.
It's called classical merely
because it has been around
for quite some
time. It
was Aristotle who came up
with the `Law of the
Excluded Middle',
which
states
that any element X, must be
either in set A or in set
not-A. It cannot be in
both. And
these two sets, set A
and set not-A should
contain the entire
universe
between
them.
Monday
Monkeys
Wednesday
Fish
Computers
Friday
Days of the
week
Figure :
Classical Set
Let's
take the example of the
set `Days of the week'.
This is a classical set
in
which
all the 7 days from
Monday up until Sunday
belong to the set,
and
everything
possible other than that
that you can think
of, monkeys,
computers,
fish,
telephone, etc, are
definitely not a part of
this set. This is a
binary
145
Artificial
Intelligence (CS607)
classification
system, in which everything
must be asserted or denied. In
the case
of Monday, it
will be asserted to be an element of
the set of `days of the
week',
but
tuna fish will not be an
element of this set.
6.3 Fuzzy
sets
Fuzzy
sets, unlike classical sets,
do not restrict themselves to
something lying
wholly in
either set A or in set
not-A. They let things
sit on the fence, and are
thus
closer to
the human world. Let
us, for example, take
into consideration `days
of
the
weekend'. The classical
set would say strictly
that only Saturday and
Sunday
are a
part of weekend, whereas
most of us would agree that
we do feel like it's
a
weekend
somewhat on Friday as well.
Actually we're more excited
about the
weekend on a
Friday than on Sunday,
because on Sunday we know
that the next
day is a working
day. This concept is more
vividly shown in the
following figure.
Thursday
Saturday
Monkeys
Tuesday
Fish
Friday
Computers
Sunday
Monday
Days of the
weekend
Figure : Fuzzy
Sets
Another
diagram that would help
distinguish between crisp and
fuzzy
representation of
days of the weekend is shown
below.
Figure : Crisp v/s
Fuzzy
The left
side of the above figure
shows the crisp set
`days of the weekend',
which
is a Boolean
two-valued function, so it gives a
value of 0 for all week
days except
Saturday
and Sunday where it gives an
abrupt 1 and then back to 0 as
soon as
Sunday
ends. On the other hand,
Fuzzy set is a multi-valued
function, which in
this
case is shown by a smoothly
rising curve for the
weekend, and even
Friday
has a
good membership in the set
`days of the
weekend'.
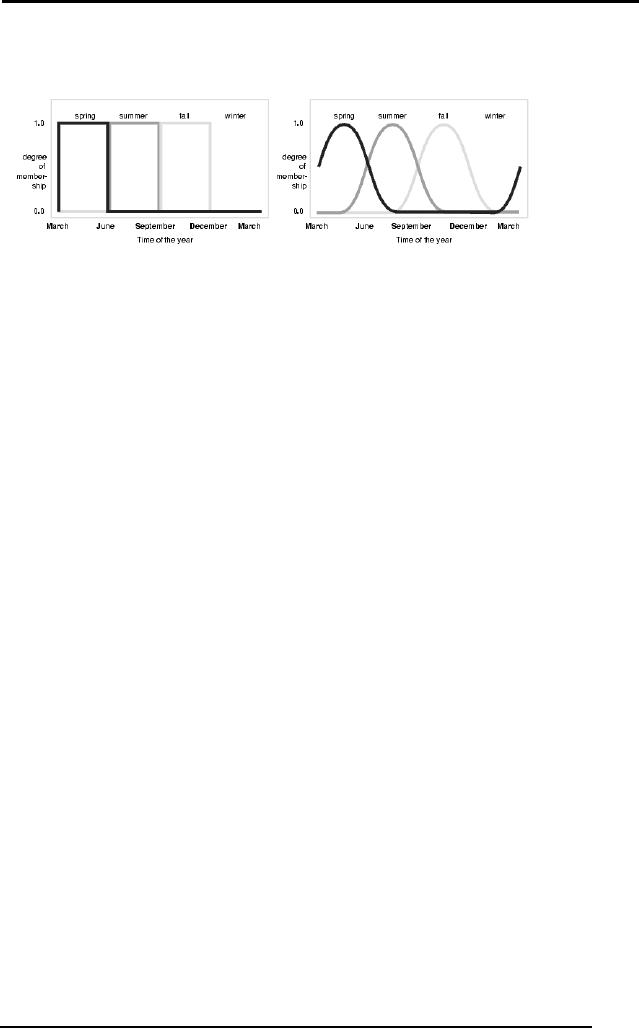
Same is
the case with seasons.
There are four seasons in
Pakistan: Spring,
Summer,
Fall and Winter. The classical/crisp
set would mark a hard
boundary
146
Artificial
Intelligence (CS607)
between
the two adjacent seasons,
whereas we know that this is
not the case in
reality.
Seasons gradually change
from one into the
next. This is more
clearly
explained in
the figure below.
Figure: Seasons [Left: Crisp]
[Right: Fuzzy]
This
entire discussion brings us to a
question: What is fuzzy
logic?
6.4 Fuzzy
Logic
Fuzzy
logic is a superset of conventional
(Boolean) logic that has
been extended
to handle
the concept of partial truth
-- truth values between
"completely true" and
"completely
false".
Dr.
Lotfi Zadeh of UC/Berkeley
introduced it in the 1960's as a
means to model
the
uncertainty of natural languages. He
was faced with a lot of
criticism but
today
the vast number of fuzzy
logic applications speak for
themselves:
� Self-focusing
cameras
� Washing
machines that adjust
themselves according to the
dirtiness of the
clothes
� Automobile
engine controls
� Anti-lock
braking systems
� Color
film developing
systems
� Subway
control systems
� Computer
programs trading successfully in
financial markets
6.4.1 Fuzzy logic
represents partial truth
Any statement
can be fuzzy. The tool that
fuzzy reasoning gives is the
ability to
reply to a
yes-no question with a
not-quite-yes-or-no answer. This is
the kind of
thing
that humans do all the
time (think how rarely
you get a straight answer to
a
seemingly
simple question; what time
are you coming home? Ans:
soon. Q: are
you coming?
Ans: I might) but it's a
rather new trick for
computers.
How does it
work? Reasoning in fuzzy
logic is just a matter of
generalizing the
familiar
yes-no (Boolean) logic. If we
give "true" the numerical
value of 1 and
"false"
the numerical value of 0,
we're saying that fuzzy
logic also permits
in-
between
values like 0.2 and
0.7453.
"In
fuzzy logic, the truth of
any statement becomes matter
of degree"
We will
understand the concept of
degree or partial truth by
the same example of
days of
the weekend. Following are
some questions and their
respective
answers:
Q: Is Saturday a
weekend day?
147
Artificial
Intelligence (CS607)
A: 1 (yes, or
true)
Q: Is Tuesday a
weekend day?
A: 0 (no, or
false)
Q: Is Friday a
weekend day?
A: 0.7
(for the most part
yes, but not
completely)
Q: Is Sunday a
weekend day?
A: 0.9
(yes, but not quite as
much as Saturday)
6.4.2 Boolean
versus fuzzy
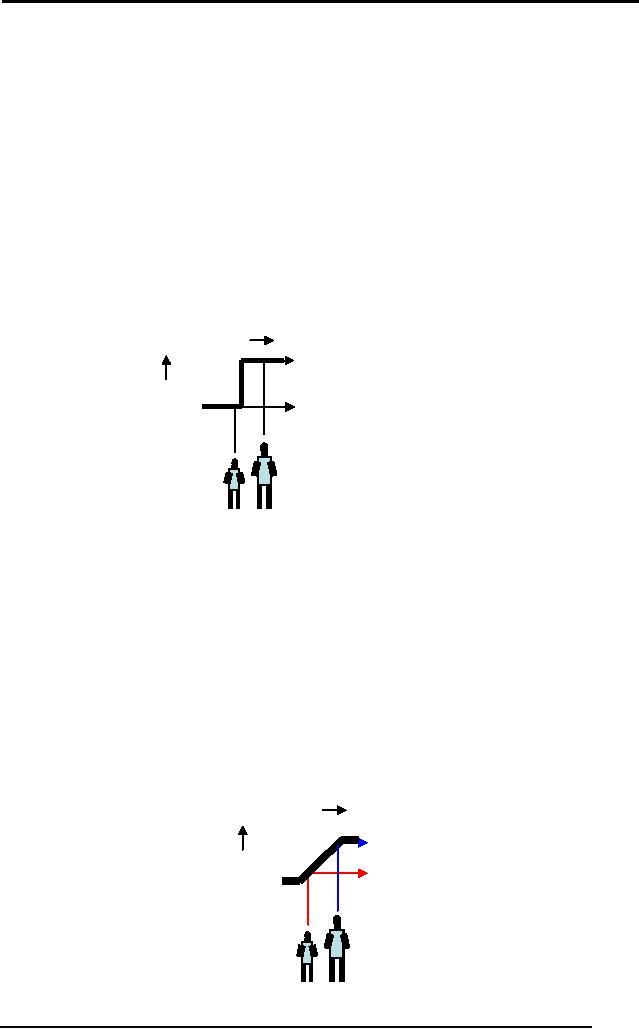
Let's
look at another comparison
between boolean and fuzzy
logic with the
help
of the
following figures. There are
two persons. Person A is
standing on the left
of
person B.
Person A is definitely shorter
than person B. But if
boolean gauge has
only
two readings, 1 and 0, then a
person can be either tall or
short. Let's say if
the
cut off point is at 5 feet
10 inches then all the
people having a height
greater
than
this limit are taller and
the rest are
short.
height
1.
Tall
0
(1.0)
Degree
of
0.
Not
Tall
tallness0
(0.0)
Figure: Boolean
Logic
On the
other hand, in fuzzy logic,
you can define any function
represented by any
mathematical
shape. The output of the
function can be discreet or
continuous.
The output of
the function defines the
membership of the input or
the degree of
truth. As in
this case, the same
person A is termed as `Not
very tall'. This
isn't
absolute
`Not tall' as in the case of
boolean. Similarly, person B is
termed as
`Quite
Tall' as apposed to the
absolute `Tall' classification by
the boolean
parameters. In
short, fuzzy logic lets us
define more realistically
the true functions
that
define real world
scenarios.
height
1.
Quite
Tall
0
(0.8)
Degree
Not
Very Tall
of
0.
(0.2)
tallness0
148
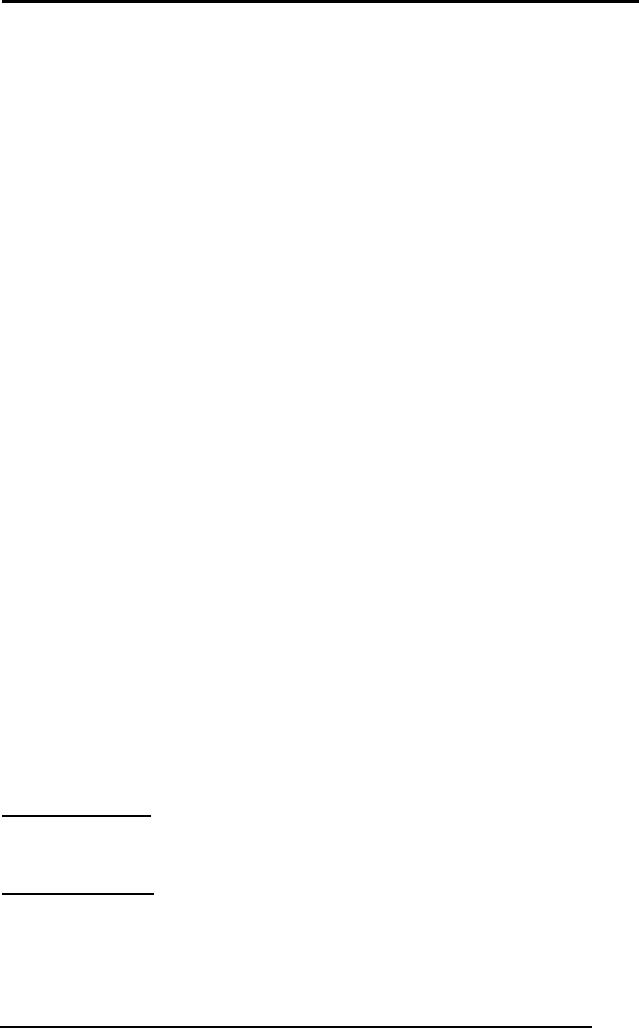
Artificial
Intelligence (CS607)
Figure: Fuzzy
Logic
6.4.3 Membership
Function (
)
The degree of
truth that we have been
talking about, is specifically
driven out by
a function
called the membership
function. It can be any function
ranging from a
simple
linear straight line to a
complicated spline function or a
polynomial of a
higher
degree.
Some
characteristics of the membership
functions are:
� It is
represented by the Greek
symbol
� Truth
values range between 0.0 and
1.0
o Where
0.0 normally represents
absolute falseness
o And 1.0
represent absolute
truth
Consider
the following
sentence:
"Amma ji is
old"
In (crisp)
set terminology, Amma ji belongs to
the set of old people. We
define
OLD,
the membership function
operating on the fuzzy set
of old people. OLD
takes as
input one variable, which is
age, and returns a value
between 0.0 and
1.0.
If Amma
ji's age is 75 years
� We might
say OLD(Amma
ji's age) = 0.75
Meaning
Amma ji is quite old
For
Amber, a 20 year old:
� We might
say OLD(Amber's
age) = 0.2
Meaning
that Amber is not very
old
For
this particular age, the
membership function is defined by a
linear line with
positive
slope.
6.4.4 Fuzzy vs.
probability
It's
important to distinguish at this
point the difference between
probability and
fuzzy, as
both operate over the
same range [0.0 to 1.0]. To
understand their
differences
lets take into account
the following case, where
Amber is a 20 years
old
girl.
OLD(Amber) =
0.2
In probability
theory:
There is a 20%
chance
that
Amber belongs to the set of
old people, there's
an
80% chance
that
she doesn't belong to the
set of old people.
In fuzzy
terminology:
Amber is
definitely not old or some
other term corresponding to
the value 0.2.
But
there
are certainly no chances
involved, no guess work left
for the system to
classify
Amber as young or
old.
149
Artificial
Intelligence (CS607)
6.4.5 Logical and
fuzzy operators
Before we
move on, let's take a
look at the logical
operators. What these
operators
help us see is that fuzzy
logic is actually a superset of
conventional
boolean
logic. This might appear to
be a startling remark at first,
but look at Table
1
below.
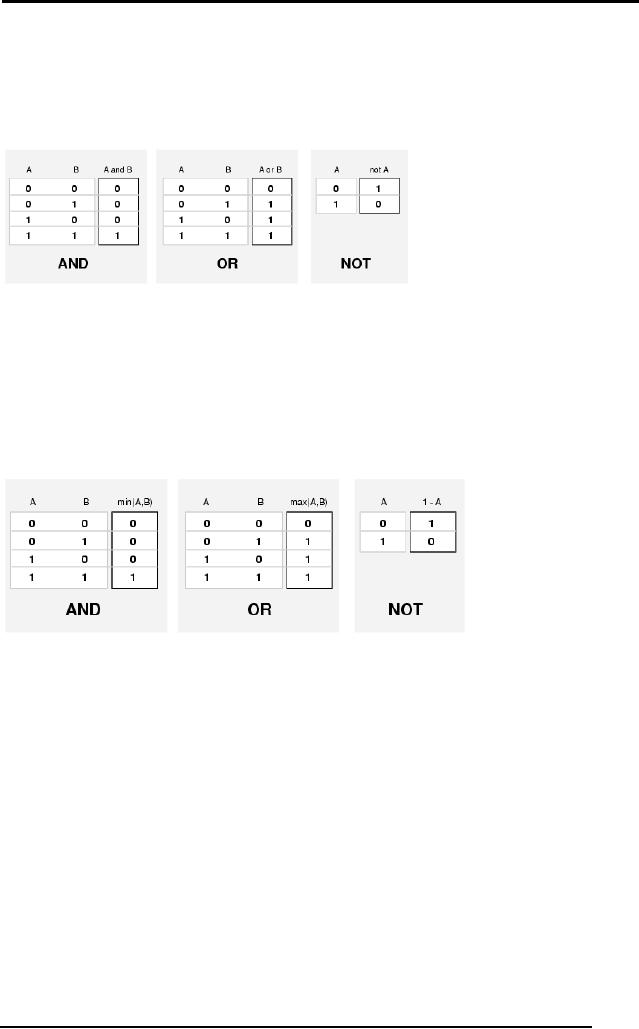
Table: Logical
Operators
The table
above lists down the AND, OR
and NOT operators and their
respective
values
for the boolean inputs. Now
for fuzzy systems we needed
the exact
operators
which would act exactly
the same way when
given the extreme
values
of 0 and 1,
and that would in addition
also act on other real
numbers between the
ranges of
0.0 to 1.0. If we choose min
(minimum) operator in place
for AND, we
get
the same output, similarly
max (maximum) operator
replaces OR, and 1-A
replaces NOT of
A.
Table: Fuzzy
Operators
In a lot of
ways these operators seem to
make sense. When we are
ANDing two
domains, A and B,
we do want to have the
intersection as a result, and
intersection
gives us the minimum
overlapping area, hence both
are equivalent.
Same is
the case with max and
1-A.
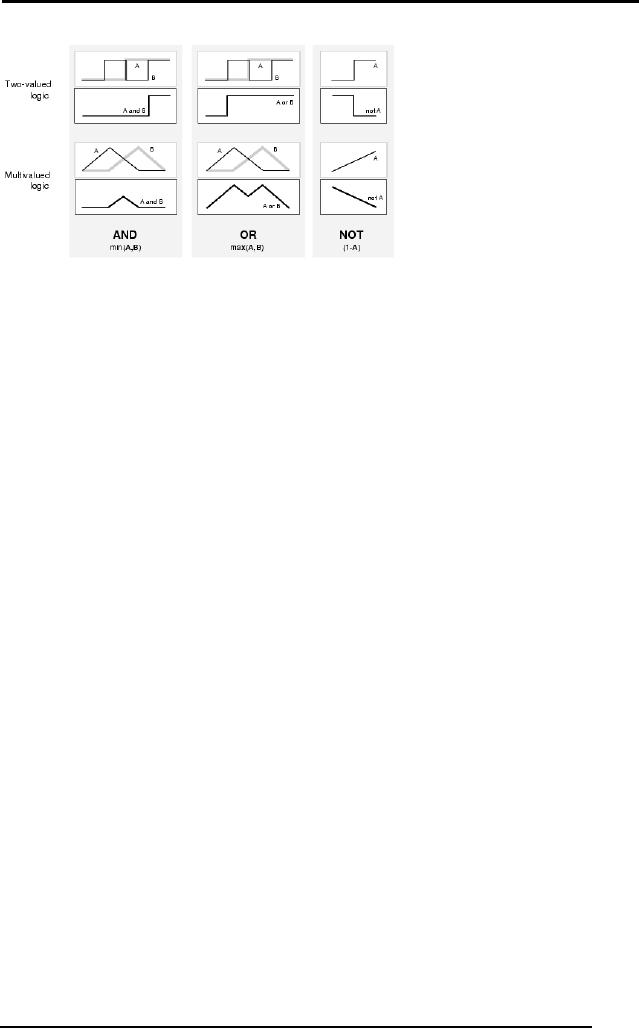
The figure
below explains these logical
operators in a non-tabular form. If
we
allow
the fuzzy system to take on
only two values, 0 and 1,
then it becomes
boolean
logic, as can be seen in the
figure, top row.
150
Artificial
Intelligence (CS607)
Figure: Logical vs Fuzzy
Operators
It would be
interesting to mention here
that the graphs for A
and B are nothing
more
than a distribution, for
instance if A was the set of
short men, then the
graph
A shows
the entire distribution of
short men where the
horizontal axis is
the
increasing
height and the vertical
axis shows the membership of
men with
different
heights in the function
`short men'. The men
who would be taller
would
have
little or 0 membership in the
function, whereas they would
have a significant
membership in
set B, considering it to be the
distribution of tall
men.
6.4.6 Fuzzy set
representation
Usually a
triangular graph is chosen to
represent a fuzzy set, with
the peak
around
the mean, which is true in
most real world scenarios,
as majority of the
population
lies around the average
height. There are fewer
men who are
exceptionally
tall or short, which
explains the slopes around
both sides of the
triangular
distribution. It's also an
approximation of the Gaussian
curve, which is
a more
general function in some
aspects.
Apart
from this graphical
representation, there's also
another representation
which is
more handy if you were to
write down some individual
members along
with
their membership. With this
representation, the set of
Tall men would be
written
like follows:
� Tall =
(0/5, 0.25/5.5, 0.8/6,
1/6.5, 1/7)
Numerator:
membership value
Denominator:
actual value of the
variable
For
instance, the first element
is 0/5 meaning, that a
height of 5 feet has
0
membership in
the set of tall people,
likewise, men who are
6.5 feet or 7 feet
tall
have a
membership value of maximum
1.
6.4.7 Fuzzy
rules
First of
all, let us revise the
concept of simple If-Then
rules. The rule is of
the
form:
If x is A then y
is B
Where x and y
are variables and A and B are
some distributions/fuzzy sets.
For
example:
If hotel
service is good then
tip is average
151

Artificial
Intelligence (CS607)
Here
hotel service is a linguistic
variable, which when given
to a real fuzzy
system
would have a certain crisp
value, maybe a rating
between 0 and 10.
This
rating
would have a membership
value in the fuzzy set of
`good'. We shall
evaluate
this rule in more detail in
the case study that
follows.
Antecedents
can have multiple
parts:
� If wind is
mild and racquets are good
then playing badminton is
fun
In this
case all parts of the
antecedent are resolved
simultaneously and resolved
to a single
number using logical
operators
The consequent
can have multiple parts as
well
� if
temperature is cold then hot
water valve is open and
cold water valve is
shut
How is the
consequent affected by the
antecedent? The consequent
specifies
that a
fuzzy set be assigned to the
output. The implication
function then
modifies
that fuzzy set to the
degree specified by the
antecedent. The most
common
ways to modify the output
fuzzy set are truncation
using the min
function
(where
the fuzzy set is "chopped
off").
Consider
the following figure, which
demonstrates the working of
fuzzy rule
system on one
rule, which states:
"If service is
excellent or food is delicious
then
tip is
generous"
Figure: Fuzzy If-Then
Rule
Fuzzify
inputs: Resolve all fuzzy
statements in the antecedent to a
degree of
membership
between 0 and 1. If there is only one
part to the antecedent, this
is
the
degree of support for the
rule. In the example, the
user gives a rating of 3
to
152

Artificial
Intelligence (CS607)
the
service, so its membership in
the fuzzy set `excellent' is
0. Likewise, the user
gives a
rating of 8 to the food, so it
has a membership of 0.7 in
the fuzzy set of
delicious.
Apply
fuzzy operator to multiple
part antecedents: If there
are multiple parts to
the
antecedent,
apply fuzzy logic operators
and resolve the antecedent to a
single
number
between 0 and 1. This is the
degree of support for the
rule. In the
example,
there are two parts to
the antecedent, and they
have an OR operator in
between
them, so they are resolved
using the max operator and
max(0,0,0.7) is
0.7.
That becomes the output of
this step.
Apply
implication method: Use the
degree of support for the
entire rule to shape
the
output fuzzy set. The
consequent of a fuzzy rule
assigns an entire fuzzy set
to
the
output. This fuzzy set is
represented by a membership function
that is chosen
to indicate
the qualities of the
consequent. If the antecedent is
only partially true,
(i.e., is
assigned a value less than
1), then the output
fuzzy set is
truncated
according to
the implication
method.
In general,
one rule by itself doesn't
do much good. What's needed
are two or
more
rules that can play
off one another. The output
of each rule is a fuzzy
set.
The output
fuzzy sets for each
rule are then aggregated
into
a single output fuzzy
set.
Finally the resulting set is
defuzzified, or resolved to a
single number. The
next
section shows how the
whole process works from
beginning to end for
a
particular
type of fuzzy inference
system.
6.5 Fuzzy
inference system
Fuzzy
inference system (FIS) is
the process of formulating
the mapping from a
given
input to an output using
fuzzy logic. This mapping
then provides a basis
from
which decisions can be made,
or patterns discerned
Fuzzy
inference systems have been
successfully applied in fields
such as
automatic
control, data classification,
decision analysis, expert
systems, and
computer
vision. Because of its
multidisciplinary nature, fuzzy
inference systems
are
associated with a number of
names, such as fuzzy-rule-based
systems, fuzzy
expert
systems, fuzzy modeling,
fuzzy associative memory,
fuzzy logic
controllers, and
simply (and ambiguously !!)
fuzzy systems. Since the
terms used
to describe
the various parts of the
fuzzy inference process are
far from standard,
we will
try to be as clear as possible
about the different terms
introduced in this
section.
Mamdani's
fuzzy inference method is
the most commonly seen
fuzzy
methodology.
Mamdani's method was among
the first control systems
built using
fuzzy
set theory. It was proposed
in 1975 by Ebrahim Mamdani as an
attempt to
control a
steam engine and boiler
combination by synthesizing a set of
linguistic
control
rules obtained from
experienced human operators.
Mamdani's effort was
based on
Lotfi Zadeh's 1973 paper on
fuzzy algorithms for complex
systems and
decision
processes.
153
Artificial
Intelligence (CS607)
6.5.1 Five parts
of the fuzzy inference process
Fuzzification of
the input variables
�
Application of
fuzzy operator in the
antecedent (premises)
�
Implication
from antecedent to
consequent
�
Aggregation of
consequents across the
rules
�
Defuzzification of
output
�
To help us
understand these steps,
let's do a small case
study.
6.5.2
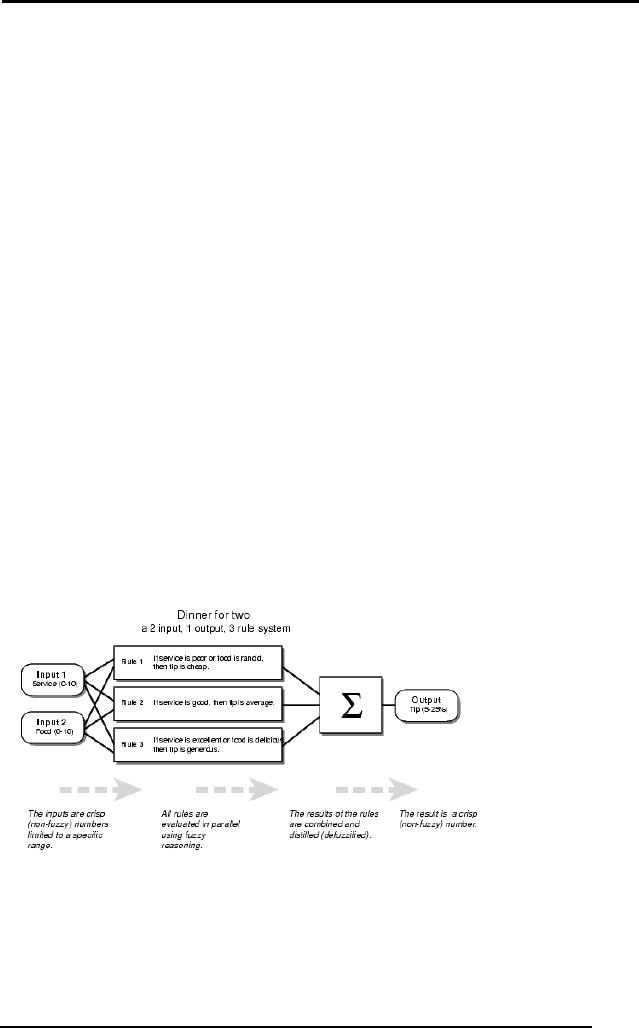
Case Study: dinner for two
We present a
small case study in which
two people go for a dinner
to a
restaurant.
Our fuzzy system will
help them decide the
percentage of tip to be
given to
the waiter (between 5 to 25
percent of the total bill),
based on their rating
of service
and food. The rating is
between 0 and 10. The system
is based on
three
fuzzy rules:
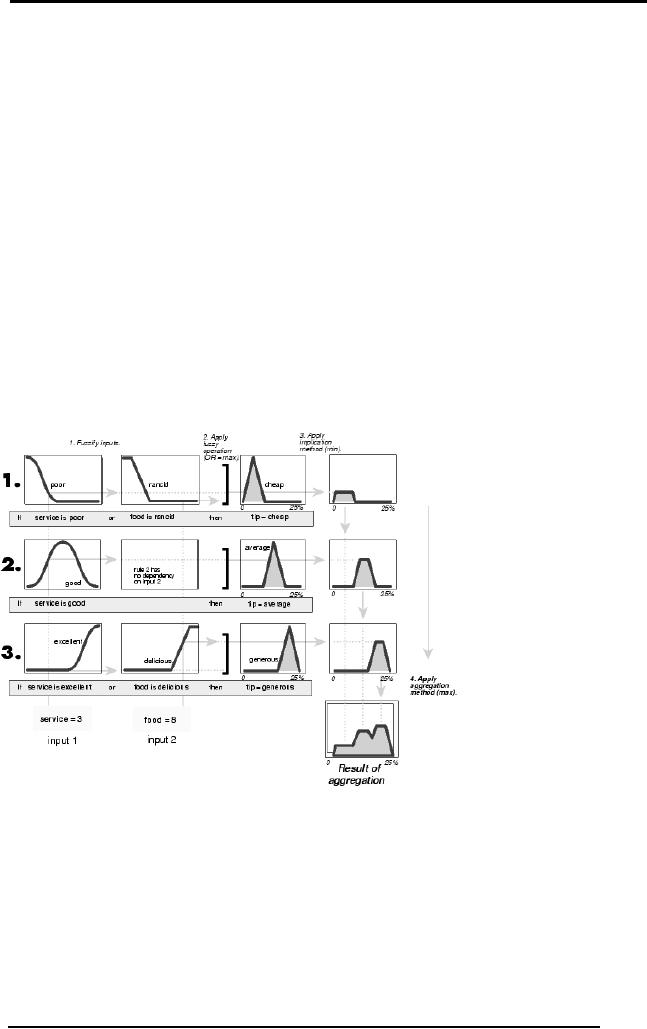
Rule1:
If service is
poor or food is rancid then
tip is cheap
Rule2:
If service is
good then tip is
average
Rule3:
If service is
excellent or food is delicious
then tip is generous
Based on
these rules and the input by
the diners, the Fuzzy
inference system
gives
the final output using
all the inference steps
listed above. Let's take a
look
at those
steps one at a time.
Figure: Dinner for
Two
6.5.2.1
Fuzzify Inputs
The first
step is to take the inputs
and determine the degree to
which they belong
to each of
the appropriate fuzzy sets
via membership functions. The
input is
154
Artificial
Intelligence (CS607)
always a
crisp numerical value
limited to the universe of
discourse of the
input
variable
(in this case the
interval between 0 and 10) and
the output is a fuzzy
degree of
membership in the qualifying
linguistic set (always the
interval between
0 and 1).
Fuzzification of the input
amounts to either a table
lookup or a function
evaluation.
The example
we're using in this section
is built on three rules, and
each of the
rules
depends on resolving the
inputs into a number of
different fuzzy
linguistic
sets:
service is poor, service is
good, food is rancid, food
is delicious, and so on.
Before
the rules can be evaluated,
the inputs must be fuzzified
according to each
of these
linguistic sets. For
example, to what extent is
the food really
delicious?
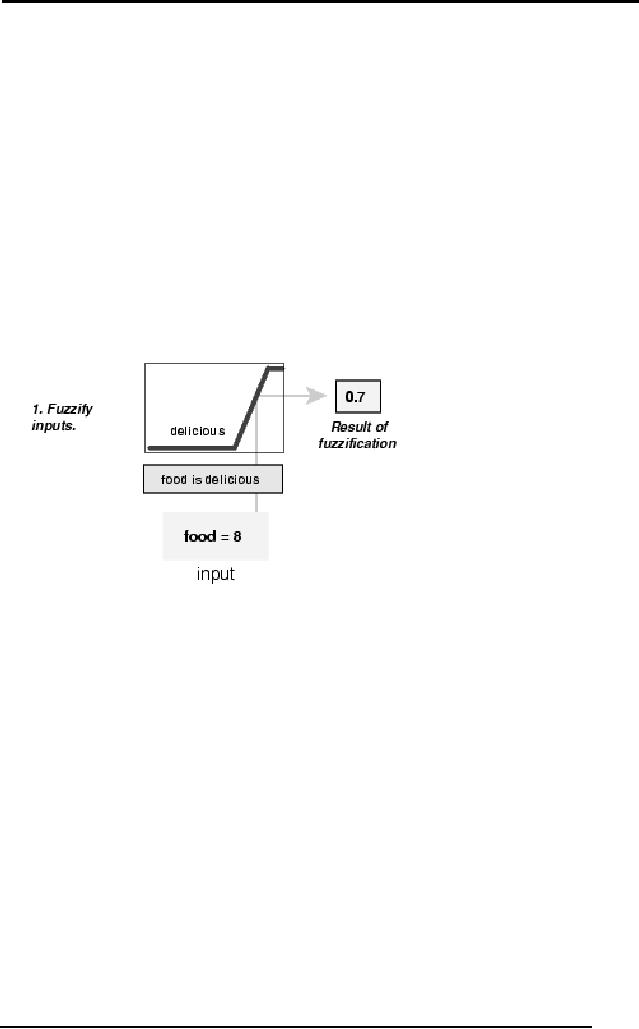
The figure
below shows how well
the food at our hypothetical
restaurant (rated on
a scale of 0 to
10) qualifies, (via its
membership function), as the
linguistic
variable
"delicious." In this case,
the diners rated the
food as an 8, which,
given
our
graphical definition of delicious,
corresponds to
= 0.7
for the "delicious"
membership
function.
Figure: Fuzzify
Input
6.5.2.2
Apply fuzzy operator
Once
the inputs have been
fuzzified, we know the
degree to which each part
of
the
antecedent has been
satisfied for each rule. If
the antecedent of a given
rule
has
more than one part, the
fuzzy operator is applied to
obtain one number
that
represents
the result of the antecedent
for that rule. This
number will then be
applied to
the output function. The
input to the fuzzy operator
is two or more
membership
values from fuzzified input
variables. The output is a single
truth
value.
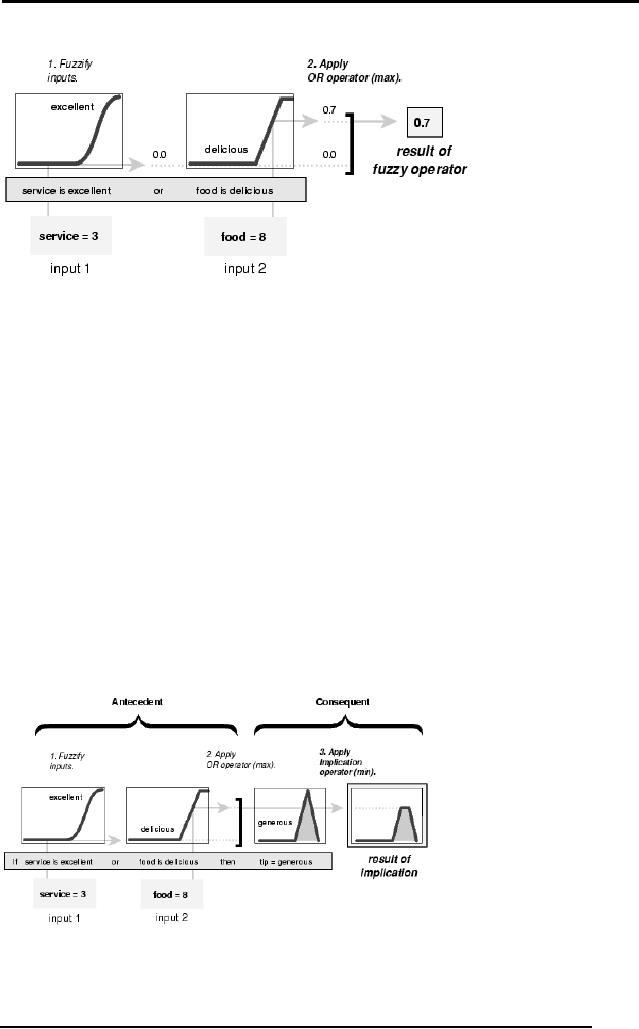
Shown
below is an example of the OR
operator max at work.
We're evaluating
the
antecedent of the rule 3 for
the tipping calculation. The
two different pieces
of
the
antecedent (service is excellent and
food is delicious) yielded
the fuzzy
membership
values 0.0 and 0.7
respectively. The fuzzy OR operator
simply
selects
the maximum of the two
values, 0.7, and the
fuzzy operation for rule 3
is
complete.
155
Artificial
Intelligence (CS607)
Figure: Apply Fuzzy
Operator
6.5.2.3
Apply implication
method
Before
applying the implication
method, we must take care of
the rule's weight.
Every
rule has a weight
(a
number between 0 and 1),
which is applied to
the
number
given by the antecedent.
Generally this weight is 1
(as it is for this
example) and so it
has no effect at all on the
implication process. From
time to
time
you may want to weigh one
rule relative to the others
by changing its
weight
value to
something other than
1.
Once
proper weightage has been
assigned to each rule, the
implication method
is implemented. A
consequent is a fuzzy set
represented by a membership
function,
which weighs appropriately
the linguistic characteristics
that are
attributed to
it. The consequent is reshaped
using a function associated
with the
antecedent (a
single number). The input
for the implication process
is a single
number
given by the antecedent, and
the output is a fuzzy set.
Implication is
implemented
for each rule. We will
use the min (minimum)
operator to perform
the
implication, which truncates
the output fuzzy set, as
shown in the figure
below.
Figure: Apply Implication
Method
156
Artificial
Intelligence (CS607)
6.5.2.4
Aggregate all outputs
Since
decisions are based on the
testing of all of the rules
in an FIS (fuzzy
inference
system), the rules must be
combined in some manner in
order to make
a decision.
Aggregation is the process by
which the fuzzy sets
that represent the
outputs of
each rule are combined
into a single fuzzy set.
Aggregation only
occurs
once for each output
variable, just prior to the
fifth and final
step,
defuzzification.
The input of the aggregation
process is the list of
truncated output
functions
returned by the implication
process for each rule. The
output of the
aggregation
process is one fuzzy set
for each output
variable.
Notice
that as long as the
aggregation method is commutative
(which it always
should
be), then the order in
which the rules are
executed is unimportant. Any
logical
operator can be used to
perform the aggregation
function: max
(maximum),
probor
(probabilistic
OR), and sum (simply
the sum of each
rule's
output
set).
In the
diagram below, all three
rules have been placed
together to show how
the
output of
each rule is combined, or
aggregated, into a single
fuzzy set whose
membership
function assigns a weighting
for every output (tip)
value.
Figure: Aggregate all
outputs
6.5.2.5
Defuzzify
The input
for the defuzzification
process is a fuzzy set (the
aggregate output
fuzzy
set) and the output is a
single number. As much as
fuzziness helps the
rule
evaluation
during the intermediate
steps, the final desired
output for each
variable
is generally a
single number. However, the
aggregate of a fuzzy
set
encompasses a
range of output values, and so
must be defuzzified in order
to
resolve a
single output value from
the set.
157
Artificial
Intelligence (CS607)
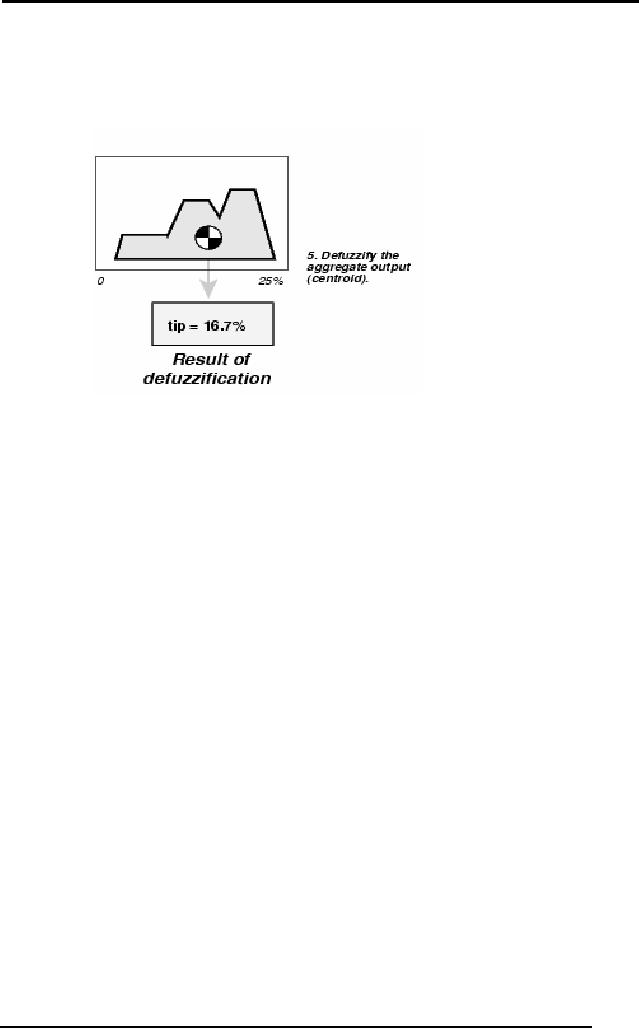
Perhaps
the most popular
defuzzification method is the
centroid calculation,
which
returns the center of area
under the curve. There
are other methods in
practice:
centroid, bisector, middle of
maximum (the average of the
maximum
value of
the output set), largest of
maximum, and smallest of
maximum.
Figure:
Defuzzification
Thus
the FIS calculates that in
case the food has a
rating of 8 and the
service
has a
rating of 3, then the tip
given to the waiter should
be 16.7% of the total
bill.
6.6
Summary
Fuzzy
system maps more
realistically, the everyday
concepts, like age,
height,
temperature
etc. The variables are given
fuzzy values. Classical
sets, either
wholly
include something or exclude it
from the membership of a
set, for instance,
in a classical
set, a man can be either
young or old. There are
crisp and rigid
boundaries
between the two age sets,
but in Fuzzy sets, there
can be partial
membership of a
man in both the
sets.
6.7
Exercise
1) Think of
the membership functions for
the following concepts, from
the
famous
quote: "Early to bed, and
early to rise, makes a man
healthy,
wealthy and
wise."
a.
Health
b.
Wealth
c.
Wisdom
2) What do you
think would be the
implication of using a different
shaped
curve
for a membership function?
For example, a triangular,
gaussian,
square
etc
3) Try to
come up with at least 5 more
rules for the tipping
system(Dinner for
two
case study), such that
the system would be a more
realistic and
complete
one.
158