Knowledge Representation and Reasoning

<< Genetic Algorithms

Expert Systems >>

Artificial Intelligence (CS607)

Lecture No. 14 -17

4 Knowledge Representation and Reasoning

Now that have looked at general problem solving, lets look at knowledge

representation and reasoning which are important aspects of any artificial

intelligence system and of any computer system in general. In this section we will

become familiar with classical methods of knowledge representation and

reasoning in AI.

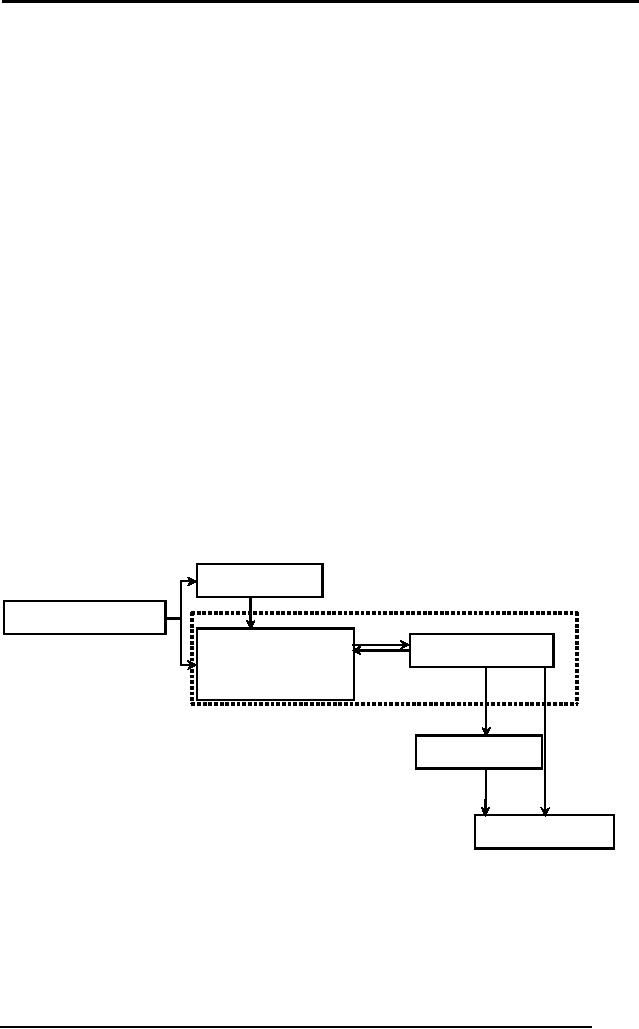
4.1 The AI Cycle

Almost all AI systems have the following components in general:

· Perception

· Learning

· Knowledge Representation and Reasoning

· Planning

· Execution

Figure 1 shows the relationship between these components.

An AI system has a perception component that allows the system to get

information from its environment. As with human perception, this may be visual,

audio or other forms of sensory information. The system must then form a

meaningful and useful representation of this information internally. This

knowledge representation maybe static or it may be coupled with a learning

component that is adaptive and draws trends from the perceived data.

LEARNING

PERCEPTION

KNOWLEDGE

REASONING

REPRESENTATION

(KR)

PLANNING

EXECUTION

Figure 1: The AI Cycle

Knowledge representation (KR) and reasoning are closely coupled components;

each is intrinsically tied to the other. A representation scheme is not meaningful

on its own; it must be useful and helpful in achieve certain tasks. The same

information may be represented in many different ways, depending on how you

want to use that information. For example, in mathematics, if we want to solve

Artificial Intelligence (CS607)

problems about ratios, we would most likely use algebra, but we could also use

simple hand drawn symbols. To say half of something, you could use 0.5x or you

could draw a picture of the object with half of it colored differently. Both would

convey the same information but the former is more compact and useful in

complex scenarios where you want to perform reasoning on the information. It is

important at this point to understand how knowledge representation and

reasoning are interdependent components, and as AI system designer, you have

to consider this relationship when coming up with any solution.

4.2 The dilemma

The key question when we begin to think about knowledge representation and

reasoning is how to approach the problem ----should we try to emulate the human

brain completely and exactly as it is? Or should we come up with something

new?

Since we do not know how the KR and reasoning components are implemented

in humans, even though we can see their manifestation in the form of intelligent

behavior, we need a synthetic (artificial) way to model the knowledge

representation and reasoning capability of humans in computers.

4.3 Knowledge and its types

Before we go any further, lets try to understand what `knowledge' is. Durkin refers

to it as the "Understanding of a subject area". A well-focused subject area is

referred to as a knowledge domain, for example, medical domain, engineering

domain, business domain, etc..

If we analyze the various types of knowledge we use in every day life, we can

broadly define knowledge to be one of the following categories:

Procedural knowledge: Describes how to do things, provides a set of

directions of how to perform certain tasks, e.g., how to drive a car.

Declarative knowledge: It describes objects, rather than processes. What

is known about a situation, e.g. it is sunny today, and cherries are red.

Meta knowledge: Knowledge about knowledge, e.g., the knowledge that

blood pressure is more important for diagnosing a medical condition than

eye color.

Heuristic knowledge: Rule-of-thumb, e.g. if I start seeing shops, I am close

to the market.

o Heuristic knowledge is sometimes called shallow knowledge.

o Heuristic knowledge is empirical as opposed to deterministic

Structural knowledge: Describes structures and their relationships. e.g.

how the various parts of the car fit together to make a car, or knowledge

structures in terms of concepts, sub concepts, and objects.

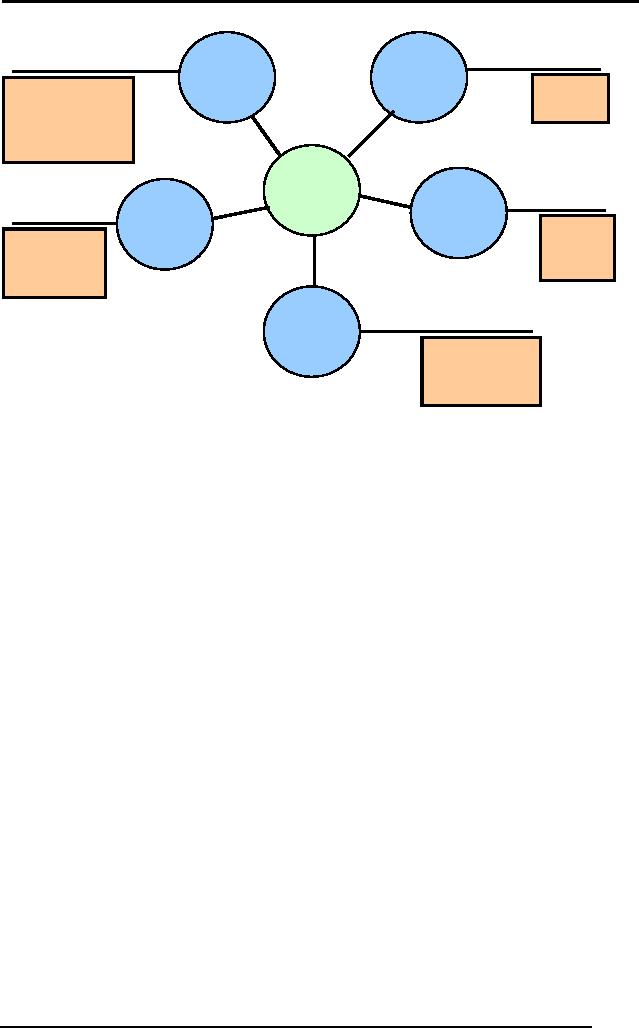
Artificial Intelligence (CS607)

Structural

Declarative

Knowledge

Objects

Relationships

Facts

between

Objects,

Concepts

Knowledge

Heuristic

Procedural

Knowledge

Rules

Knowledge

Rules

Procedure

Thumb

Methods

Meta-

Knowledge

about

Knowledge

Fig 2: Types of Knowledge

4.4 Towards Representation

There are multiple approaches and schemes that come to mind when we begin to

think about representation

Pictures and symbols. This is how the earliest humans represented

knowledge when sophisticated linguistic systems had not yet evolved

Graphs and Networks

Numbers

4.4.1 Pictures

Each type of representation has its benefits. What types of knowledge is best

represented using pictures? , e.g. can we represent the relationship between

individuals in a family using a picture? We could use a series of pictures to store

procedural knowledge, e.g. how to boil an egg. But we can easily see that

pictures are best suited for recognition tasks and for representing structural

information. However, pictorial representations are not very easily translated to

useful information in computers because computers cannot interpret pictures

directly with out complex reasoning. So even though pictures are useful for

human understanding, because they provide a high level view of a concept to be

obtained readily, using them for representation in computers is not as straight

forward.

4.4.2 Graphs and Networks

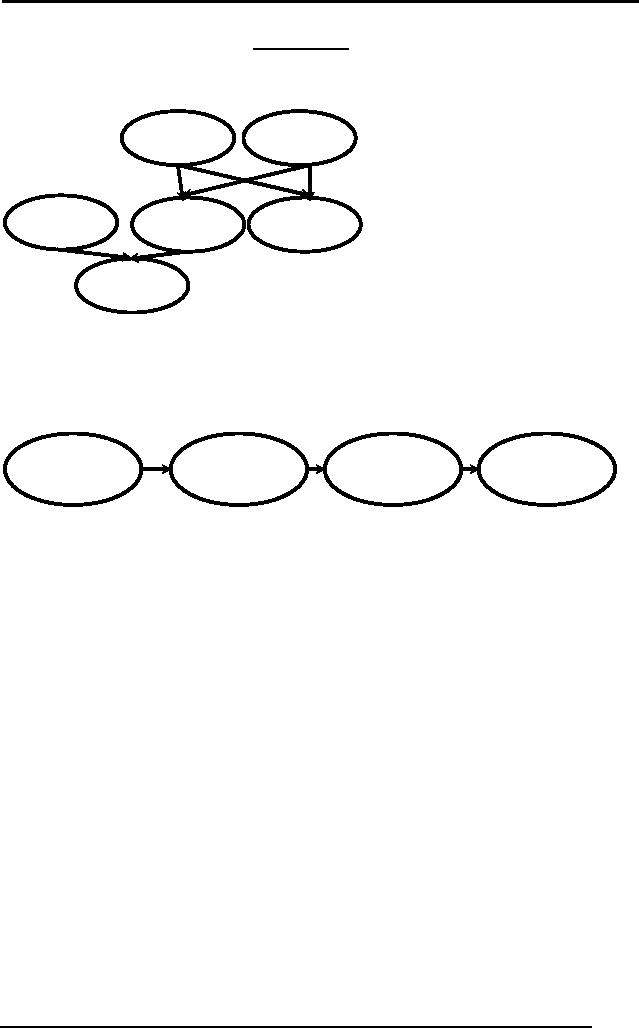
Artificial Intelligence (CS607)

Graphs and Networks allow relationships between objects/entities to be

incorporated, e.g., to show family relationships, we can use a graph.

Tariq

Ayesha

Hassan

Amina

Mona

Ali

Fig 3: Family Relationships

We can also represent procedural knowledge using graphs, e.g. How to start a

car?

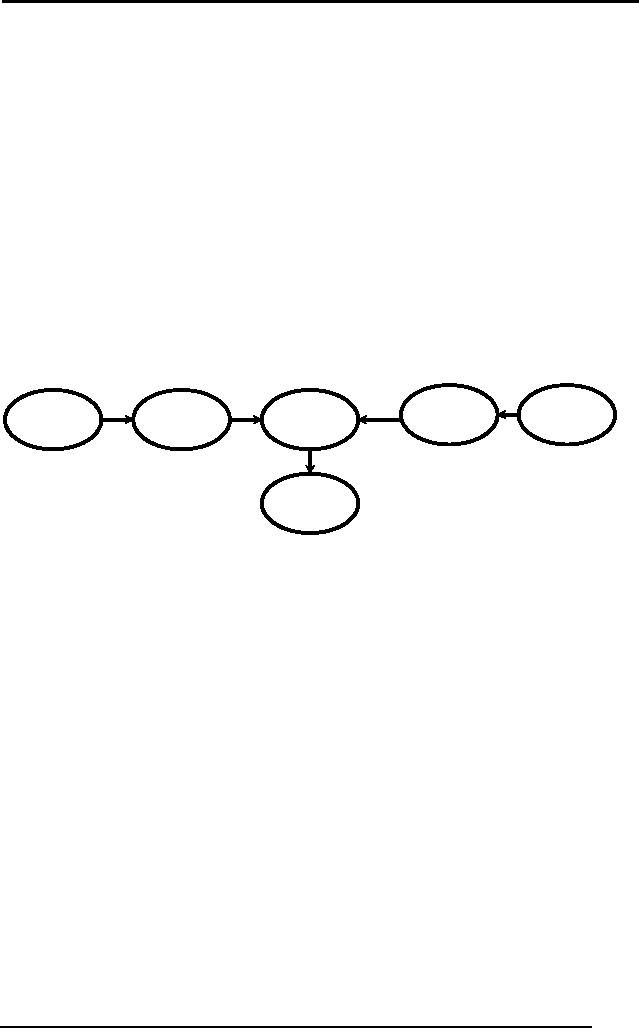
Insert Key

Turn Ignition

Press Clutch

Set Gear

Fig 4: Graph for procedural knowledge

4.4.3 Numbers

Numbers are an integral part of knowledge representation used by humans.

Numbers translate easily to computer representation. Eventually, as we know,

every representation we use gets translated to numbers in the computers internal

representation.

4.4.4 An Example

In the context of the above discussion, let's look at some ways to represent the

knowledge of a family

Using a picture

Artificial Intelligence (CS607)

Fig 5: Family Picture

As you can see, this kind of representation makes sense readily to humans, but if

we give this picture to a computer, it would not have an easy time figuring out the

relationships between the individuals, or even figuring out how many individuals

are there in the picture. Computers need complex computer vision algorithms to

understand pictures.

Using a graph

Ayesha

Tariq

Mona

Fig 6: Family graph

This representation is more direct and highlights relationships.

Using a description in words

For the family above, we could say in words

Tariq is Mona's Father

Ayesha is Mona's Mother

Mona is Tariq and Ayesha's Daughter

This example demonstrates the fact that each knowledge representation scheme

has its own strengths and weaknesses.

4.5 Formal KR techniques

In the examples above, we explored intuitive ways for knowledge representation.

Now, we will turn our attention to formal KR techniques in AI. While studying

these techniques, it is important to remember that each method is suited to

representing a certain type of knowledge. Choosing the proper representation is

Artificial Intelligence (CS607)

important because it must help in reasoning. As the saying goes `Knowledge is

Power'.

4.6 Facts

Facts are a basic block of knowledge (the atomic units of knowledge). They

represent declarative knowledge (they declare knowledge about objects). A

proposition is the statement of a fact. Each proposition has an associated truth

value. It may be either true or false. In AI, to represent a fact, we use a

proposition and its associated truth value, e.g.

Proposition A: It is raining

Proposition B: I have an umbrella

Proposition C: I will go to school

4.6.1 Types of facts

Single-valued or multiple valued

Facts may be single-valued or multi-valued, where each fact (attribute) can take

one or more than one values at the same time, e.g. an individual can only have

one eye color, but may have many cars. So the value of attribute cars may

contain more than one value.

Uncertain facts

Sometimes we need to represent uncertain information in facts. These facts are

called uncertain facts, e.g. it will probably be sunny today. We may chose to store

numerical certainty values with such facts that tell us how much uncertainty there

is in the fact.

Fuzzy facts

Fuzzy facts are ambiguous in nature, e.g. the book is heavy/light. Here it is

unclear what heavy means because it is a subjective description. Fuzzy

representation is used for such facts. While defining fuzzy facts, we use certainty

factor values to specify value of "truth". We will look at fuzzy representation in

more detail later.

Object-Attribute-Value triplets

Object-Attribute Value Triplets or OAV triplets are a type of fact composed of

three parts; object, attribute and value. Such facts are used to assert a particular

property of some object, e.g.

Ali's eye color is brown.

o Object: Ali

o Attribute: eye color

Artificial Intelligence (CS607)

o Value: brown

Ahmed's son is Ali

o Object: Ahmed

o Attribute: son

o Value: Ali

OAV Triplets are also defined as in figure below

Eye Color

Ali

Brown

Object

Attribute

Value

Color

Ahmed

Red

Object

Attribute

Value

Figure: OAV Triplets

4.7 Rules

Rules are another form of knowledge representation. Durkin defines a rule as "A

knowledge structure that relates some known information to other information

that can be concluded or inferred to be true."

4.7.1 Components of a rule

A Rule consists of two components

o Antecedent or premise or the IF part

o Consequent or conclusion or the THEN part

For example, we have a rule: IF it is raining THEN I will not go to school

Premise: It is raining

Conclusion: I will not go to school.

4.7.2 Compound Rules

Multiple premises or antecedents may be joined using AND (conjunctions) and

OR (disjunctions), e.g.

IF it is raining AND I have an umbrella

THEN I will go to school.

IF it is raining OR it is snowing

THEN I will not go to school

Artificial Intelligence (CS607)

4.7.3 Types of rules

Relationship

Relationship rules are used to express a direct occurrence relationship between

two events, e.g. IF you hear a loud sound THEN the silencer is not working

Recommendation

Recommendation rules offer a recommendation on the basis of some known

information, e.g.

IF it is raining

THEN bring an umbrella

Directive

Directive rules are like recommendations rule but they offer a specific line of

action, as opposed to the `advice' of a recommendation rule, e.g.

IF it is raining AND you don't have an umbrella

THEN wait for the rain to stop

Variable Rules

If the same type of rule is to be applied to multiple objects, we use variable rules,

i.e.

rules

with

variables,

e.g.

Student

AND

X's

GPA>3.7

THEN place X on honor roll.

Such rules are called pattern-matching rules. The rule is matched with known

facts and different possibilities for the variables are tested, to determine the truth

of the fact.

Uncertain Rules

Uncertain rules introduce uncertain facts into the system, e.g.

IF you have never won a match

THEN you will most probably not win this time.

Meta Rules

Meta rules describe how to use other rules, e.g.

IF you are coughing AND you have chest congestion

THEN use the set of respiratory disease rules.

Rule Sets

Artificial Intelligence (CS607)

As in the previous example, we may group rules into categories in our knowledge

representation scheme, e.g. the set of respiratory disease rules

4.8 Semantic networks

Semantic networks are graphs, with nodes representing objects and arcs

representing relationships between objects. Various types of relationships may

be defined using semantic networks. The two most common types of

relationships are

IS-A (Inheritance relation)

HAS (Ownership relation)

Let's consider an example semantic network to demonstrate how knowledge in a

semantic network can be used

IS-A

Truck

Bedford

Suzuki

Car

Vehicle

Travels by

Road

Figure: Vehicle Semantic Network

Network Operation

To infer new information from semantic networks, we can ask questions from

nodes

Ask node vehicle: `How do you travel?'

This node looks at arc and replies: road

Ask node Suzuki: `How do you travel?'

This node does not have a link to travel therefore it asks other

nodes linked by the IS-A link

Asks node Car (because of IS-A relationship)

Asks node Vehicle (IS-A relationship)

Node Vehicle Replies: road

Problems with Semantic Networks

o Semantic networks are computationally expensive at run-time as we need

to traverse the network to answer some question. In the worst case, we

may need to traverse the entire network and then discover that the

requested info does not exist.

o They try to model human associative memory (store information using

associations), but in the human brain the number of neurons and links are

Artificial Intelligence (CS607)

in the order of 1015. It is not practical to build such a large semantic

network, hence this scheme is not feasible for this type of problems.

o Semantic networks are logically inadequate as they do not have any

equivalent quantifiers, e.g., for all, for some, none.

4.9 Frames

"Frames are data structures for representing stereotypical knowledge of some

concept or object" according to Durkin, a frame is like a schema, as we would call

it in a database design. They were developed from semantic networks and later

evolved into our modern-day Classes and Objects. For example, to represent a

student, we make use of the following frame:

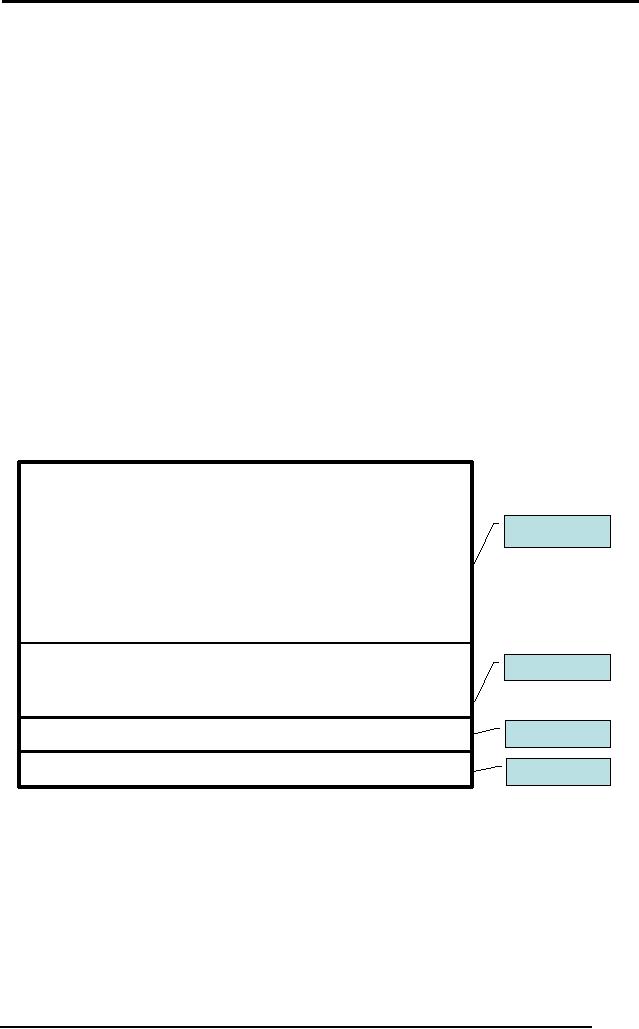
Frame Name: Student

Properties:

Age: 19

GPA: 4.0

Ranking: 1

Figure: Student Frame

The various components within the frame are called slots, e.g. Frame Name slot.

4.9.1 Facets

A slot in a frame can hold more that just a value, it consists of metadata and

procedures also. The various aspects of a slot are called facets. They are a

feature of frames that allows us to put constraints on frames. e.g. IF-NEEDED

Facets are called when the data of a particular slot is needed. Similarly, IF-

CHANGED Facets are when the value of a slot changes.

4.10 Logic

Just like algebra is a type of formal logic that deals with numbers, e.g. 2+4 = 6,

propositional logic and predicate calculus are forms of formal logic for dealing

with propositions. We will consider two basic logic representation techniques:

Propositional Logic

Predicate Calculus

4.10.1

Propositional logic

A proposition is the statement of a fact. We usually assign a symbolic variable to

represent a proposition, e.g.

Artificial Intelligence (CS607)

p = It is raining

q = I carry an umbrella

A proposition is a sentence whose truth values may be determined. So, each

proposition has a truth value, e.g.

The proposition `A rectangle has four sides' is true

The proposition `The world is a cube' is false.

4.10.1.1

Compound statements

Different propositions may be logically related and we can form compound

statements of propositions using logical connectives. Common logical

connectives are:

AND (Conjunction)

∧

OR (Disjunction)

∨

NOT (Negation)

If ... then (Conditional)

→

If and only if (bi-conditional)

⇔

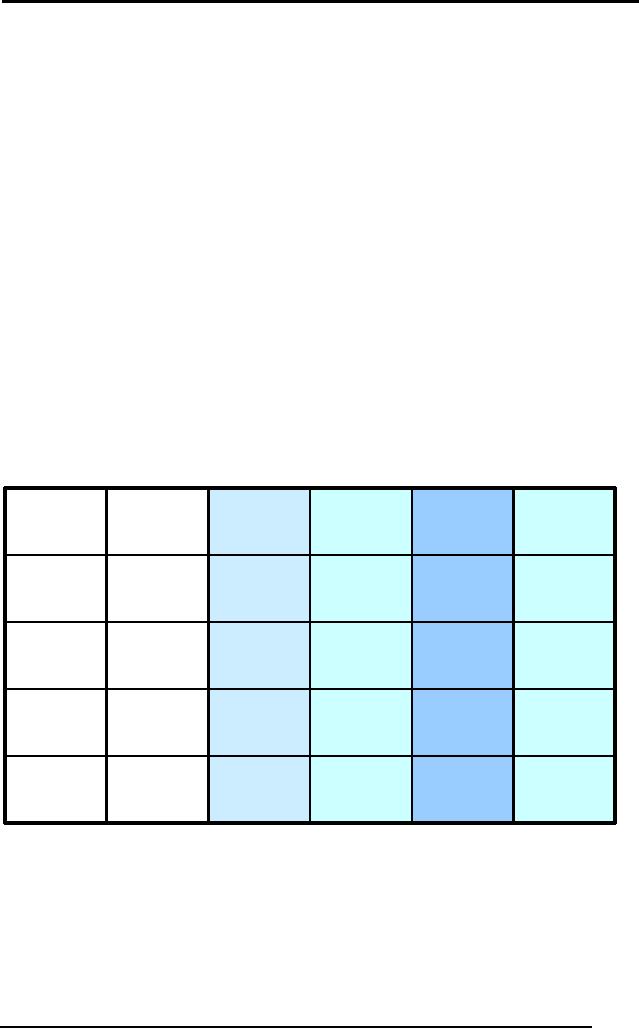
The table below shows the logic of the above connectives

p ∧q

p∨q

p⇒q

p⇔q

Figure: Truth Table of Binary Logical Connectives

4.10.1.2

Limitations of propositional logic

o Propositions can only represent knowledge as complete sentences, e.g.

a = the ball's color is blue.

o Cannot analyze the internal structure of the sentence.

Artificial Intelligence (CS607)

o No quantifiers are available, e.g. for-all, there-exists

o Propositional logic provides no framework for proving statements such as:

All humans are mortal

All women are humans

Therefore, all women are mortals

This is a limitation in its representational power.

4.10.2

Predicate calculus

Predicate Calculus is an extension of propositional logic that allows the structure

of facts and sentences to be defined. With predicate logic, we can use

expressions like

Color( ball, blue)

This allows the relationship of sub-sentence units to be expressed, e.g. the

relationship between color, ball and blue in the above example. Due to its greater

representational power, predicate calculus provides a mechanism for proving

statements and can be used as a logic system for proving logical theorems.

4.10.2.1

Quantifiers

Predicate calculus allows us to use quantifiers for statements. Quantifiers allow

us to say things about some or all objects within some set. The logical quantifiers

used in basic predicate calculus are universal and existential quantifiers.

The Universal quantifier

The symbol for the universal quantifier is ∀ It is read as "for every" or "for all" and

used in formulae to assign the same truth value to all variables in the domain,

e.g. in the domain of numbers, we can say that ( ∀ x) ( x + x = 2x). In words this

is: for every x (where x is a number), x + x = 2x is true. Similarly, in the domain of

shapes, we can say that ( ∀ x) (x = square → x = polygon), which is read in

words as: every square is a polygon. In other words, for every x (where x is a

shape), if x is a square, then x is a polygon (it implies that x is a polygon).

Existential quantifier

The symbol for the existential quantifier is ∃ . It is read as "there exists", " for

some", "for at least one", "there is one", and is used in formulae to say that

something is true for at least one value in the domain, e.g. in the domain of

persons, we can say that

( ∃ x) (Person (x) ∧ father (x, Ahmed) ). In words this reads as: there exists some

person, x who is Ahmed's father.

4.10.2.2

First order predicate logic

100

Artificial Intelligence (CS607)

First order predicate logic is the simplest form of predicate logic. The main types

of symbols used are

Constants are used to name specific objects or properties, e.g. Ali, Ayesha,

blue, ball.

Predicates: A fact or proposition is divided into two parts

Predicate: the assertion of the proposition

Argument: the object of the proposition

For example, the proposition "Ali likes bananas" can be represented in predicate

logic as Likes (Ali, bananas), where Likes is the predicate and Ali and bananas

are the arguments.

Variables: Variables are used to a represent general class of objects/properties,

e.g. in the predicate likes (X, Y), X and Y are variables that assume the values

X=Ali and Y=bananas

Formulae:

Formulas

combine

predicates

and

quantifiers

represent

information

Lets us illustrate these symbols using an example

man(ahmed)

father(ahmed, belal)

brother(ahmed, chand)

Predicates

owns(belal, car)

tall(belal)

hates(ahmed, chand)

family()

∀ Y (¬sister(Y,ahmed))

Formulae

∀X,Y,Z(man(X) ∧ man(Y) man(Z) ∧ father(Z,Y)

∧ father(Z,X) ⇒ brother(X,Y))

X, Y and Z

Variables

ahmed, belal, chand and car

Constants

Figure : Predicate Logic Example

The predicate section outlines the known facts about the situation in the form of

predicates, i.e. predicate name and its arguments. So, man(ahmed) means that

ahmed is a man, hates(ahmed, chand) means that ahmed hates chand.

101

Artificial Intelligence (CS607)

The formulae sections outlines formulae that use universal quantifiers and

variables to define certain rules. ∀ Y (¬sister(Y,ahmed)) says that there exists

no Y such that Y is the sister of ahmed, i.e. ahmed has no sister. Similarly,

∀X,Y,Z(man(X) ∧ man(Y) man(Z) ∧ father(Z,Y) ∧ father(Z,X) ⇒ brother(X,Y))

means that if there are three men, X, Y and Z, and Z is the father of both X

and Y, then X and Y are bothers. This expresses the rule for the two

individuals being brothers.

4.11 Reasoning

Now that we have looked at knowledge representation, we will look at

mechanisms to reason on the knowledge once we have represented it using

some logical scheme. Reasoning is the process of deriving logical conclusions

from given facts. Durkin defines reasoning as `the process of working with

knowledge, facts and problem solving strategies to draw conclusions'.

Throughout this section, you will notice how representing knowledge in a

particular way is useful for a particular kind of reasoning.

4.12 Types of reasoning

We will look at some broad categories of reasoning

4.12.1.1

Deductive reasoning

Deductive reasoning, as the name implies, is based on deducing new information

from logically related known information. A deductive argument offers assertions

that lead automatically to a conclusion, e.g.

If there is dry wood, oxygen and a spark, there will be a fire

Given: There is dry wood, oxygen and a spark

We can deduce: There will be a fire.

All men are mortal. Socrates is a man.

We can deduce: Socrates is mortal

4.12.2

Inductive reasoning

Inductive reasoning is based on forming, or inducing a `generalization' from a

limited set of observations, e.g.

Observation: All the crows that I have seen in my life are black.

Conclusion: All crows are black

Comparison of deductive and inductive reasoning

We can compare deductive and inductive reasoning using an example. We

conclude what will happen when we let a ball go using both each type of

reasoning in turn

102

Artificial Intelligence (CS607)

The inductive reasoning is as follows: By experience, every time I have let a ball

go, it falls downwards. Therefore, I conclude that the next time I let a ball go, it

will also come down.

The deductive reasoning is as follows: I know Newton's Laws. So I conclude

that if I let a ball go, it will certainly fall downwards.

Thus the essential difference is that inductive reasoning is based on experience

while deductive reasoning is based on rules, hence the latter will always be

correct.

4.12.3

Abductive reasoning

Deduction is exact in the sense that deductions follow in a logically provable way

from the axioms. Abduction is a form of deduction that allows for plausible

inference, i.e. the conclusion might be wrong, e.g.

Implication: She carries an umbrella if it is raining

Axiom: she is carrying an umbrella

Conclusion: It is raining

This conclusion might be false, because there could be other reasons that she is

carrying an umbrella, e.g. she might be carrying it to protect herself from the sun.

4.12.4

Analogical reasoning

Analogical reasoning works by drawing analogies between two situations, looking

for similarities and differences, e.g. when you say driving a truck is just like

driving a car, by analogy you know that there are some similarities in the driving

mechanism, but you also know that there are certain other distinct characteristics

of each.

4.12.5

Common-sense reasoning

Common-sense reasoning is an informal form of reasoning that uses rules gained

through experience or what we call rules-of-thumb. It operates on heuristic

knowledge and heuristic rules.

4.12.6

Non-Monotonic reasoning

Non-Monotonic reasoning is used when the facts of the case are likely to change

after some time, e.g.

Rule:

IF the wind blows

THEN the curtains sway

When the wind stops blowing, the curtains should sway no longer. However, if we

use monotonic reasoning, this would not happen. The fact that the curtains are

swaying would be retained even after the wind stopped blowing. In non-

103

Artificial Intelligence (CS607)

monotonic reasoning, we have a `truth maintenance system'. It keeps track of

what caused a fact to become true. If the cause is removed, that fact is removed

(retracted) also.

4.12.7

Inference

Inference is the process of deriving new information from known information. In

the domain of AI, the component of the system that performs inference is called

an inference engine. We will look at inference within the framework of `logic',

which we introduced earlier

4.12.7.1

Logic

Logic, which we introduced earlier, can be viewed as a formal language. As a

language, it has the following components: syntax, semantics and proof systems.

Syntax

Syntax is a description of valid statements, the expressions that are legal in that

language. We have already looked at the syntax of two type of logic systems

called propositional logic and predicate logic. The syntax of proposition gives us

ways to use propositions, their associated truth value and logical connectives to

reason.

Semantics

Semantics pertain to what expressions mean, e.g. the expression `the cat drove

the car' is syntactically correct, but semantically non-sensible.

Proof systems

A logic framework comes with a proof system, which is a way of manipulating

given statements to arrive at new statements. The idea is to derive `new'

information from the given information.

Recall proofs in math class. You write down all you know about the situation and

then try to apply all the rules you know repeatedly until you come up with the

statement you were supposed to prove. Formally, a proof is a sequence of

statements aiming at inferring some information. While doing a proof, you usually

proceed with the following steps:

You begin with initial statements, called premises of the proof (or knowledge

base)

Use rules, i.e. apply rules to the known information

Add new statements, based on the rules that match

Repeat the above steps until you arrive at the statement you wished to prove.

4.12.7.1.1

Rules of inference

104

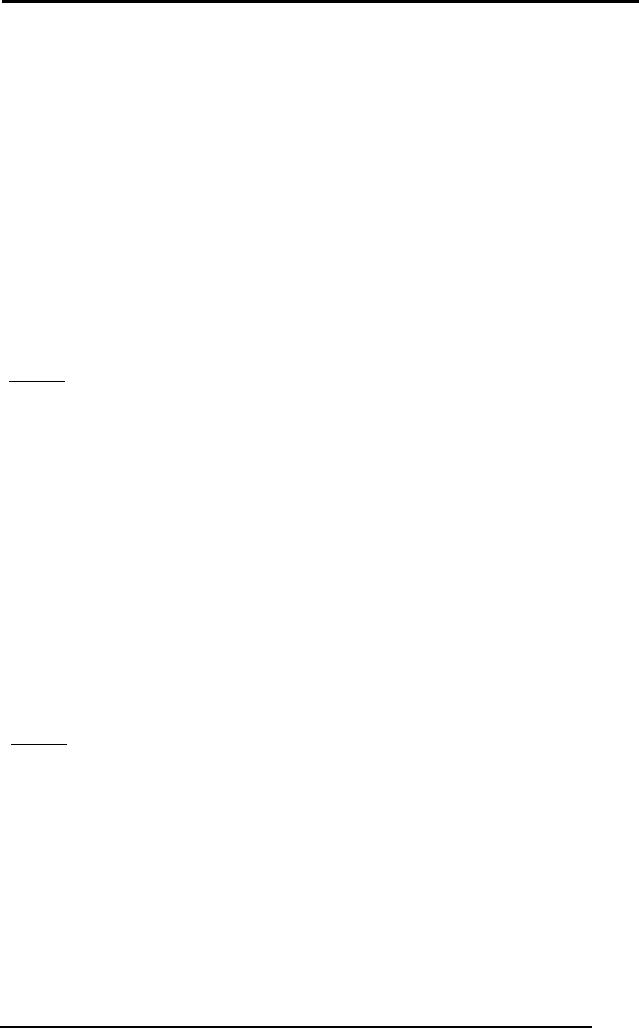
Artificial Intelligence (CS607)

Rules of inference are logical rules that you can use to prove certain things. As

you look at the rules of inference, try to figure out and convince yourself that the

rules are logically sound, by looking at the associated truth tables. The rules we

will use for propositional logic are:

Modus Ponens

Modus Tolens

And-Introduction

And-Elimination

Modus ponens

"Modus ponens" means "affirming method". Note: From now on in our discussion

of logic, anything that is written down in a proof is a statement that is true.

α →β

Modus-

Ponens

Modus Ponens says that if you know that alpha implies beta, and you know alpha

to be true, you can automatically say that beta is true.

Modus Tolens

Modus Tolens says that "alpha implies beta" and "not beta" you can conclude

"not alpha". In other words, if Alpha implies beta is true and beta is known to be

not true, then alpha could not have been true. Had alpha been true, beta would

automatically have been true due to the implication.

α →β

¬β

¬α

Modus -

Tolens

And-Introduction and and-Elimination

And-introduction say that from "Alpha" and from "Beta" you can conclude "Alpha

and Beta". That seems pretty obvious, but is a useful tool to know upfront.

Conversely, and-elimination says that from "Alpha and Beta" you can conclude

"Alpha".

105

Artificial Intelligence (CS607)

α ∧β

And-

elimination

Introduction

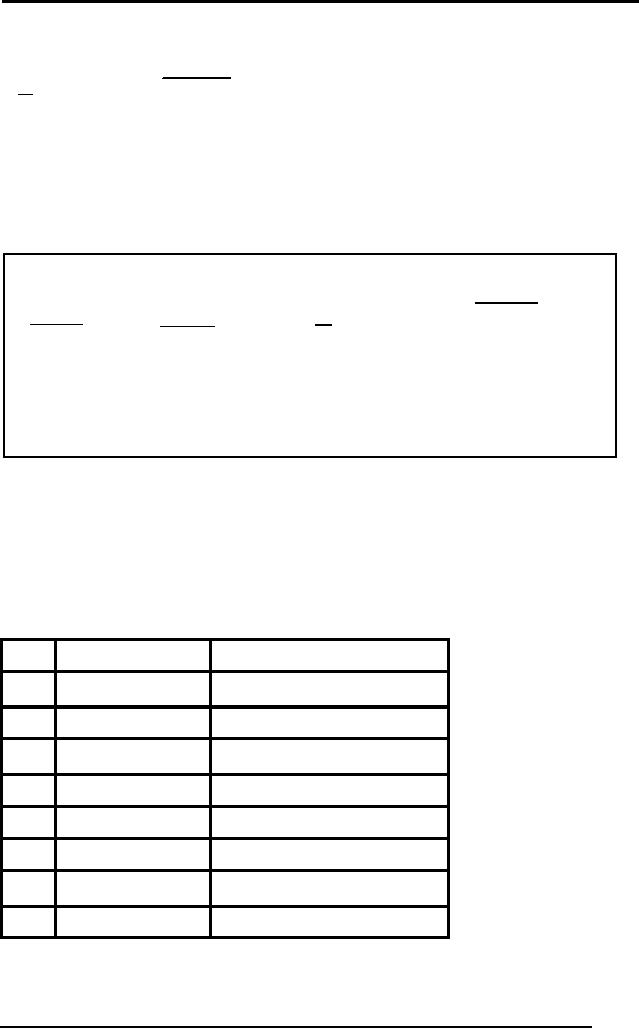
The table below gives the four rules of inference together:

α ∧β

α →β

¬β

¬α

α ∧β

And-

Modus

And-

Modus

elimination

Ponens

Introduction

Tolens

Figure : Table of Rules of Inference

4.12.7.2

Inference example

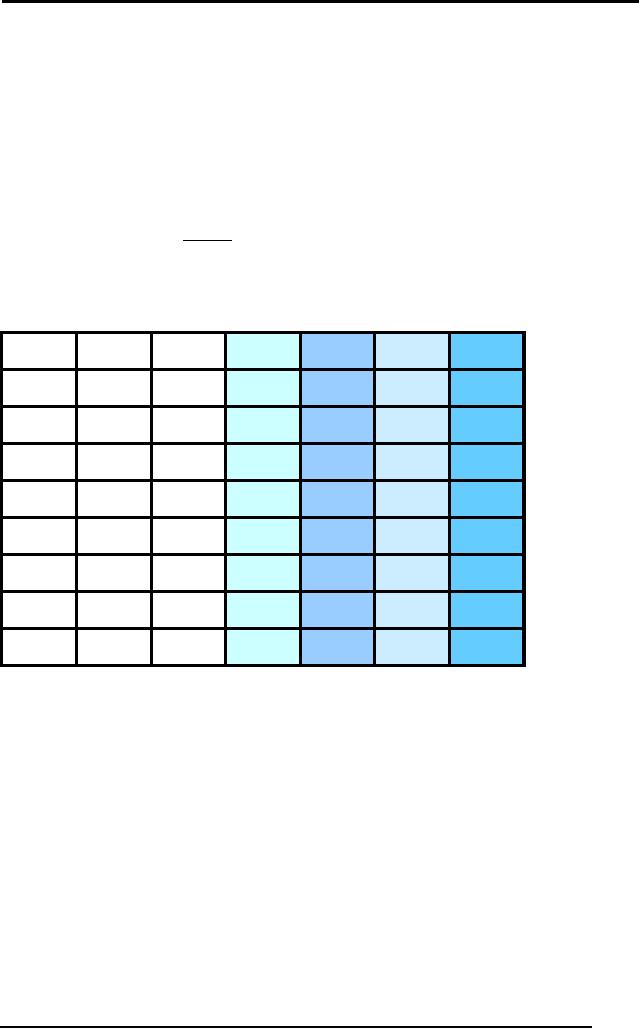
Now, we will do an example using the above rules. Steps 1, 2 and 3 are added

initially, they are the given facts. The goal is to prove D. Steps 4-8 use the rules

of inference to reach at the required goal from the given rules.

Step

Formula

Derivation

Given

A∧B

A→C

Given

(B ∧ C) →D

1 And-elimination

4, 2 Modus Ponens

1 And-elimination

5, 6 And-introduction

B ∧C

7, 3 Modus Ponens

Note: The numbers in the derivation reference the statements of other step

numbers.

106

Artificial Intelligence (CS607)

4.12.7.3

Resolution rule

The deduction mechanism we discussed above, using the four rules of inference

may be used in practical systems, but is not feasible. It uses a lot of inference

rules that introduce a large branch factor in the search for a proof. An alternative

is approach is called resolution, a strategy used to determine the truth of an

assertion, using only one resolution rule:

α∨β

¬β ∨ γ

α ∨γ

To see how this rule is logically correct, look at the table below:

¬β

α ∨γ

α∨β

¬β ∨ γ

You can see that the rows where the premises of the rule are true, the conclusion

of the rule is true also.

To be able to use the resolution rule for proofs, the first step is to convert all given

statements into the conjunctive normal form.

4.12.7.4

Conjunctive normal form

Resolution requires all sentences to be converted into a special form called

conjunctive normal form (CNF). A statement in conjunctive normal form (CNF)

consists of ANDs of Ors. A sentence written in CNF looks like

( A ∨ B) ∧ (B ∨ ¬C ) ∧ (D)

note : D = ( D ∨ ¬D)

107

Artificial Intelligence (CS607)

The outermost structure is made up of conjunctions. Inner units called clauses

are made up of disjunctions. The components of a statement in CNF are clauses

and literals. A clause is the disjunction of many units. The units that make up a

clause are called literals. And a literal is either a variable or the negation of a

variable. So you get an expression where the negations are pushed in as tightly

as possible, then you have ORs, then you have ANDs. You can think of each

clause as a requirement. Each clause has to be satisfied individually to satisfy the

entire statement.

4.12.7.5

Conversion to CNF

1. Eliminate arrows (implications)

A → B = ¬A ∨ B

2. Drive in negations using De Morgan's Laws, which are given below

¬( A ∨ B) = (¬A ∧ ¬B)

¬( A ∧ B) = (¬A ∨ ¬B)

3. Distribute OR over AND

A ∨ (B ∧ C)

= ( A ∨ B) ∧ ( A ∨ C )

4.12.7.6

Example of CNF conversion

( A ∨ B ) → (C → D )

1.¬( A ∨ B ) ∨ (¬C ∨ D )

2.(¬A ∧ ¬B ) ∨ (¬C ∨ D )

3.(¬A ∨ ¬C ∨ D ) ∧ (¬B ∨ ¬C ∨ D )

4.12.7.7

Resolution by Refutation

Now, we will look at a proof strategy called resolution refutation. The steps for

proving a statement using resolution refutation are:

· Write all sentences in CNF

· Negate the desired conclusion

· Apply the resolution rule until you derive a contradiction or cannot apply

the rule anymore.

· If we derive a contradiction, then the conclusion follows from the given

axioms

· If we cannot apply anymore, then the conclusion cannot be proved from

the given axioms

108

Artificial Intelligence (CS607)

4.12.8

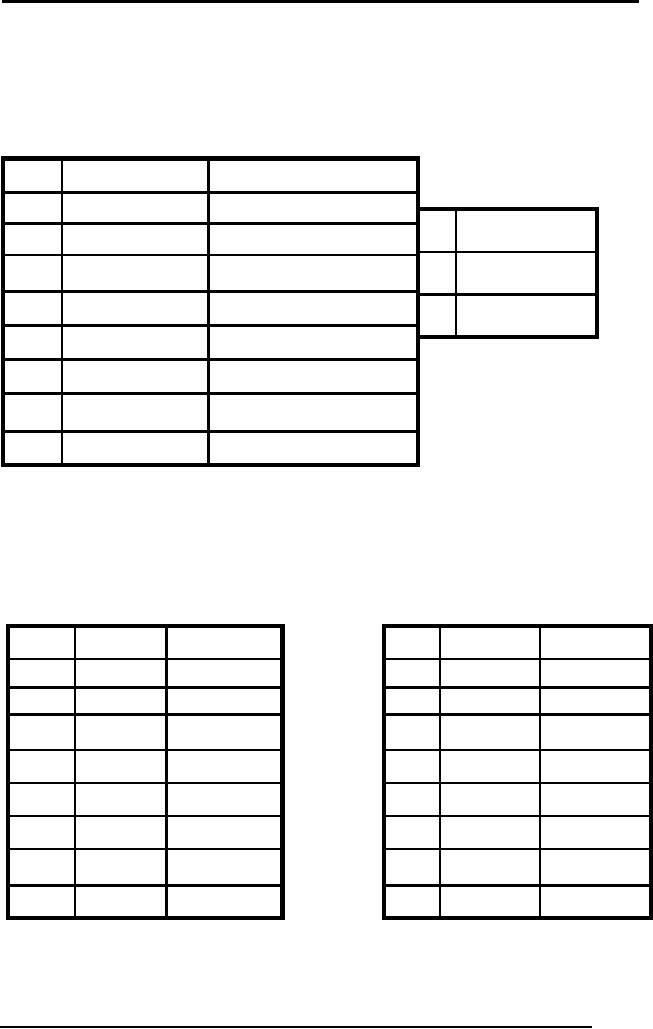
Resolution refutation example 1

Prove C

Ste

Formula

Derivation

Given

A∨B

Given

¬A ∨ C

A→C

Given

¬B ∨ C

¬C

Negated Conclusion

B →C

1, 2

B∨C

¬A

2, 4

¬B

3, 4

5, 7 Contradiction!

The statements in the table on the right are the given statements. These are

converted to CNF and are included as steps 1, 2 and 3. Our goal is to prove C.

Step 4 is the addition of the negation of the desired conclusion. Steps 5-8 use the

resolution rule to prove C.

Note that you could have come up with multiple ways of proving R:

Step

Formula

Step

Formula

Given

A∨B

Given

¬A ∨ C

Given

¬B ∨ C

¬C

¬B

3,4

1,2

B∨C

1,5

¬A

2,4

2,6

¬B

3,4

5,7

4.12.9

Resolution Refutation Example 2

109

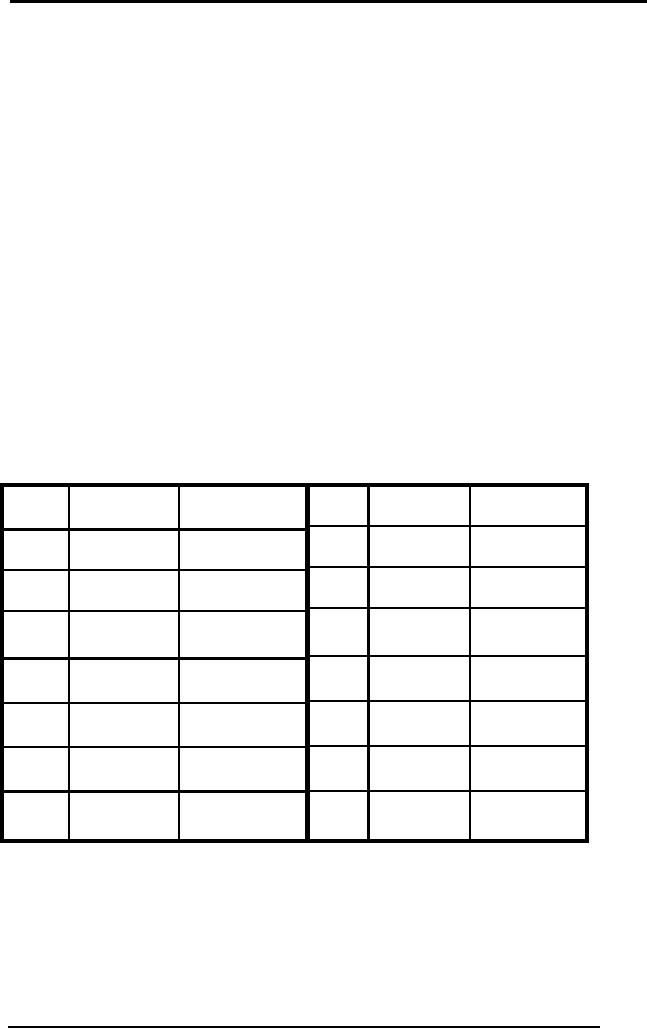
Artificial Intelligence (CS607)

1. (A→B) →B

2. A→C

3. ¬C → ¬B

Prove C

Convert to CNF

1.( A → B) → B

= (¬A ∨ B) → B

= ¬(¬A ∨ B) ∨ B

= ( A ∧ ¬B) ∨ B

= ( A ∨ B) ∧ (¬B ∨ B)

= ( A ∨ B)

2. A → C = ¬A ∨ C

3.¬C → ¬B = C ∨ ¬B

Proof

Step

Formula

Derivation

Step

Formula

Derivation

Given

B∨A

Given

B∨A

Given

¬A∨C

Given

¬A∨C

Given

C ∨ ¬B

Given

C ∨ ¬B

¬C

Negation of

¬C

conclusion

¬B

3,4

2,4

1,5

2,5

2,6

4.12.9.1

Proof strategies

As you can see from the examples above, it is often possible to apply more

than one rule at a particular step. We can use several strategies in such

cases. We may apply rules in an arbitrary order, but there are some rules of

thumb that may make the search more efficient

110

Table of Contents: