ZeePedia

Row language, Nonterminals

<< Conversion Form, Joints of the machine
Non-Context-Free language, Pumping lemma for CFLs >>
img
Theory of Automata
(CS402)
Theory of Automata
Lecture N0. 42
Reading Material
Introduction to Computer Theory
Chapter 15
Summary
Row language, nonterminals defined from summary table, productions defined by rows, rules for defining
productions, all possible productions of CFG for row language of the example under consideration, CFG
corresponding to the given PDA
Note
As has already been discussed that the Row language is the language whose alphabet
 = {Row1, Row2, ..., Row7}, for the example under consideration, so to determine the CFG of Row language,
the nonterminals of this CFG are introduced in the form Net(X, Y, Z)
where X and Y are joints and Z is any STACK character. Following is an example of Net(X, Y, Z)
a
b
Z
POP
POP
POP
PUSH a
PUSH b
If the above is the path segment between two joints then, the net STACK effect is same as POP Z.
For a given PDA, some sets of all possible sentences Net(X, Y, Z) are true, while other are false. For this
purpose every row of the summary table is examined whether the net effect of popping is exactly one letter.
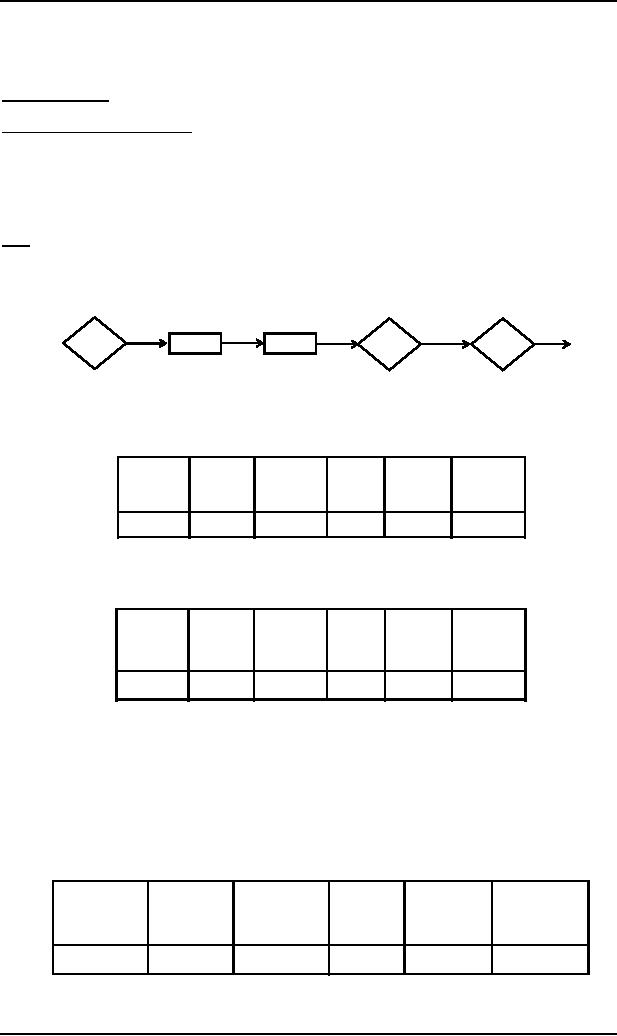
Consider the Row4 of the summary table developed for the PDA of the language {a2nbn}
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
READ1
HERE
b
a
--
4
The nonterminal corresponding to the above row may be written as Net (READ1, HERE, a) i.e.Row4 is a single
Net row.
Consider the following row from an arbitrary summary table
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
READ9
READ3
b
b
abb
11
which shows that Row11 is not Net style sentence because the trip from READ9 to READ3 does not pop one
letter form the STACK, while it adds two letters to the STACK. However Row11 can be concatenated with some
other Net style sentences e.g. Row11Net(READ3, READ7, a)Net(READ7, READ1, b)Net(READ1, READ8, b)
Which gives the nonterminal
Net(READ9, READ8, b), now the whole process can be written as
Net(READ9, READ8, b) Æ Row11Net(READ3, READ7,a) Net(READ7, READ1, b)Net(READ1, READ8, b)
Which will be a production in the CFG of the corresponding row language.
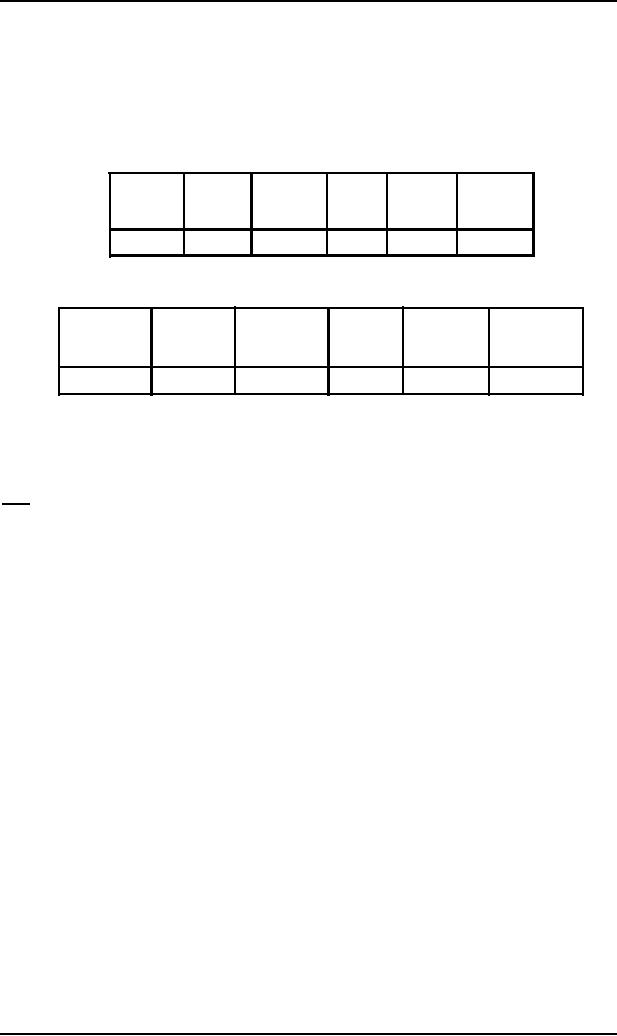
In general to create productions from rows of summary table, consider the following row in certain summary
table
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
READx
READy
u
w
i
m1m2...mn
then for any sequence of joint states S1, S2, ...Sn, the production in the row language can be included as
129
img
Theory of Automata
(CS402)
Net(READx, Sn, w) Æ RowiNet(READy, S1, m1)...Net(Sn-1, Sn, mn)
It may be noted that in CFG, in general, replacing a nonterminal with string of some other nonterminals does not
always lead to a word in the corresponding CFL e.g. S Æ X|Y, X Æ ab, Y Æ aYY
Here Y Æ aYY does not lead to any word of the language.
Following are the three rules of defining all possible productions of CFG of the row language
The trip starting from START state and ending in ACCEPT state with the NET style
Net(START, ACCEPT, $) gives the production of the form S Æ Net(START, ACCEPT, $)
From the summary table the row of the following form
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
X
Y
anything
z
i
--
Defines the productions of the form Net(X,Y,z) Æ Rowi
For each row that pushes string of characters on to the STACK of the form
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
READx
READy
u
w
i
m1m2...mn
then for any sequence of joint states S1, S2, ...Sn, the production in the row language can be included as
Net(READX,Sn, w) Æ RowiNet(READY, S1,m1) ...Net(Sn-1, Sn, mn)
It may be noted that this rule introduces new productions. It does not mean that each production of the form
Nonterminal Æ string of nonterminals, helps in defining some word of the language.
Note
Considering the example of PDA accepting the language {a2nbn:n=1, 2, 3, ...}, using rule1, rule2 and rule3 the
possible productions for the CFG of the row language are
S Æ Net(START, ACCEPT, $)
Net(READ1, HERE, a) Æ Row4
Net(HERE, READ2, a) Æ Row5
Net(READ2, HERE, a) Æ Row6
Net(READ2, ACCEPT, $) Æ Row7
Net(START, READ1, $) Æ Row1Net(READ1, READ1, $)
Net(START, READ2, $) Æ Row1Net(READ1,READ2, $)
Net(START, HERE, $) Æ Row1Net(READ1, HERE, $)
Net(START, ACCEPT, $) Æ Row1Net(READ1, ACCEPT, $)
Net(READ1, READ1, $) Æ Row2Net( READ1, READ1, a)Net(READ1, READ1, $)
Net(READ1, READ1, $) Æ Row2Net( READ1, READ2, a)Net(READ2, READ1, $)
Net(READ1, READ1, $) Æ Row2Net( READ1, HERE, a)Net(HERE, READ1, $)
Net(READ1, READ2, $) Æ Row2Net( READ1, READ1, a)Net(READ1, READ2, $)
Net(READ1, READ2, $) Æ Row2Net( READ1, READ2, a)Net(READ2, READ2, $)
Net(READ1, READ2, $) Æ Row2Net( READ1, HERE, a)Net(HERE, READ2, $)
Net(READ1, HERE, $) Æ Row2Net( READ1, READ1, a)Net(READ1, HERE, $)
Net(READ1, HERE, $) Æ Row2Net( READ1, READ2, a)Net(READ2, HERE, $)
Net(READ1, HERE, $) Æ Row2Net( READ1, HERE, a)Net(HERE, HERE, $)
Net(READ1, ACCEPT, $) Æ Row2Net( READ1,READ1,a)Net(READ1,ACCEPT, $)
Net(READ1,ACCEPT, $) Æ Row2Net( READ1,READ2,a)Net(READ2,ACCEPT, $)
Net(READ1, ACCEPT, $) Æ Row2Net( READ1, HERE, a)Net(HERE, ACCEPT, $)
Net(READ1, READ1, a) Æ Row3Net( READ1, READ1, a)Net(READ1, READ1, a)
Net(READ1, READ1, a) Æ Row3Net( READ1, READ2, a)Net(READ2, READ1, a)
Net(READ1, READ1, a) Æ Row3Net( READ1, HERE, a)Net(HERE, READ1, a)
Net(READ1, READ2, a) Æ Row3Net( READ1, READ1, a)Net(READ1, READ2, a)
Net(READ1, READ2, a) Æ Row3Net( READ1, READ2, a)Net(READ2, READ2, a)
Net(READ1, READ2, a) Æ Row3Net( READ1, HERE, a)Net(HERE, READ2, a)
Net(READ1, HERE, a) Æ Row3Net( READ1, READ1, a)Net(READ1, HERE, a)
Net(READ1, HERE, a) Æ Row3Net( READ1, READ2, a)Net(READ2, HERE, a)
130
img
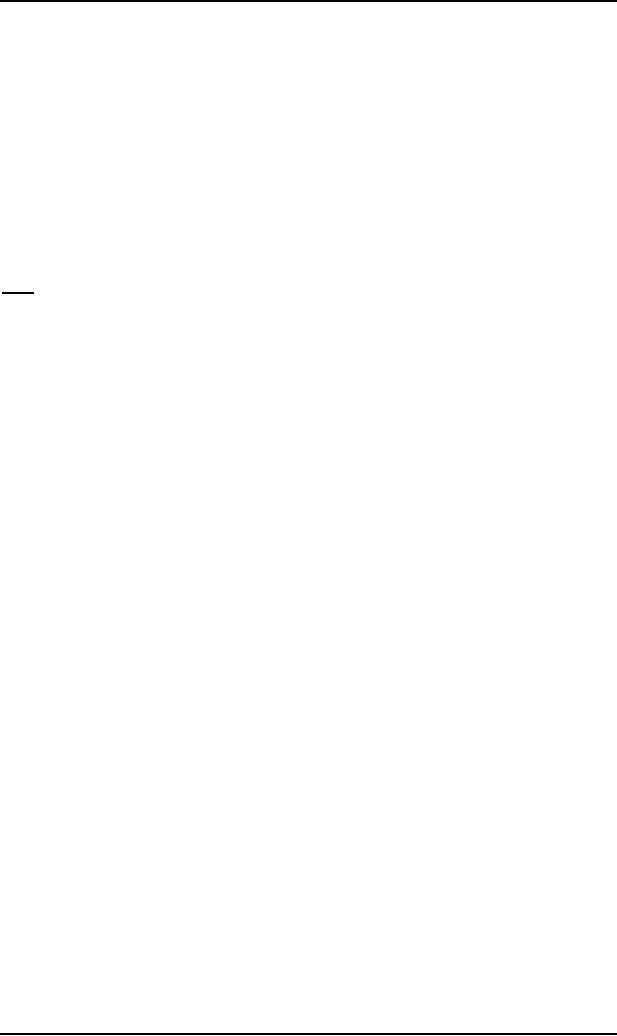
Theory of Automata
(CS402)
Net(READ1, HERE, a) Æ Row3Net( READ1, HERE, a)Net(HERE, HERE, a)
Net(READ1, ACCEPT, a) Æ Row3Net( READ1, READ1,a)Net(READ1,ACCEPT,a)
Net(READ1, ACCEPT, a) Æ Row3Net( READ1, READ2,a)Net(READ2,ACCEPT,a)
Net(READ1, ACCEPT, a) Æ Row3Net (READ1, HERE,a)Net(HERE,ACCEPT,a)
Following is a left most derivation of a word of row language
fi Net(START, ACCEPT, $)
S
...
using 1
fi Row1Net(READ1, ACCEPT, $)
...
using 9
fi Row1Row2Net(RD1,RD2, a)Net(RD2,AT, $)
...
using 20
fi Row1Row2Row3Net(RD1, HERE,a)Net (RD2,HERE,a)Net(RD2,AT,$)...
using 27
fi Row1Row2Row3Row4Net(HERE, RD2, a)Net(RD2, ACCEPT, $)
...
using 2
fi Row1Row2Row3Row4Row5Net(HERE, ACCEPT, $)
...
using 3
fi Row1Row2Row3Row4Row5Row7
...
using 5
Which is the shortest word in the whole row language.
It can be observed that each left most derivation generates the sequence of rows of the summary table, which are
both joint- and STACK- consistent.
Note: So far the rules have been defined to create all possible productions for the CFG of the row language.
Since in each row in the summary table, the READ column contains L and D in addition to the letters of the
alphabet of the language accepted by the PDA, so each word of the row language generates the word of the
language accepted by the given PDA.
Thus the following rule 4 helps in completing the CFG corresponding to the given PDA
Each row of the summary table defines a production of the form Rowi Æ a where in Rowi the READ column
consists of letter a.
Application of rule 4 to the summary table for the PDA accepting {a2nbn : n=1,2,3,...} under consideration adds
the following productions
Row1 Æ L
Row2 Æ a
Row3 Æ a
Row4 Æ b
Row5 Æ L
Row6 Æ b
Row7 Æ D
Which shows that the word Row1Row2Row3Row4Row5Row7 of the row language is converted to LaabLD = abb
131
Table of Contents:
  1. What does automata mean, Introduction to languages
  2. Kleene Star Closure, Recursive definition of languages
  3. Regular Expression, Recursive definition of Regular Expression
  4. Equivalent Regular Expressions
  5. Finite Automaton
  6. Equivalent FAs
  7. FA corresponding to finite languages
  8. Examples of TGs: accepting all strings
  9. Generalized Transition Graphs
  10. Nondeterminism, Kleene’s Theorem
  11. Proof(Kleene’s Theorem Part II)
  12. Kleene’s Theorem Part III
  13. Concatenation of FAs
  14. Closure of an FA
  15. Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
  16. NFA with Null String
  17. NFA and Kleene’s Theorem
  18. NFA corresponding to Concatenation of FAs
  19. Distinguishable strings and Indistinguishable strings
  20. Finite Automaton with output, Moore machine
  21. Mealy machine
  22. Equivalent machines
  23. Mealy machines in terms of sequential circuit
  24. Regular languages, Complement of a language
  25. Nonregular languages
  26. Pumping Lemma
  27. Pumping Lemma version II
  28. Pseudo theorem
  29. Decidability
  30. finiteness of a language
  31. Context Free Grammar (CFG), CFG terminologies
  32. Trees
  33. Polish Notation (o-o-o)
  34. Total language tree, Regular Grammar
  35. Null Production
  36. Chomsky Normal Form (CNF)
  37. A new format for FAs
  38. Nondeterministic PDA
  39. PDA corresponding to CFG
  40. Conversion form of PDA
  41. Conversion Form, Joints of the machine
  42. Row language, Nonterminals
  43. Non-Context-Free language, Pumping lemma for CFLs
  44. Decidablity, Parsing Techniques
  45. Turing machine