Conversion Form, Joints of the machine

<< Conversion form of PDA

Row language, Nonterminals >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 41

Reading Material

Introduction to Computer Theory

Chapter 15

Summary

Recap of PDA in conversion form, example of PDA in conversion form, joints of the machine, new pictorial

representation of PDA in conversion form, summary table, row sequence, row language.

Conversion form of PDA

Definition

A PDA is in conversion form if it fulfills the following conditions:

There is only one ACCEPT state.

There are no REJECT states.

Every READ or HERE is followed immediately by a POP i.e. every edge leading out of any READ or HERE

state goes directly into a POP state.

No two POPs exist in a row on the same path without a READ or HERE between them whether or not there are

any intervening PUSH states (i.e. the POP states must be separated by READs or HEREs).

All branching, deterministic or nondeterministic occurs at READ or HERE states, none at POP states and every

edge has only one label.

Even before we get to START, a "bottom of STACK" symbol $ is placed on the STACK. If this symbol is ever

popped in the processing it must be replaced immediately. The STACK is never popped beneath this symbol.

Right before entering ACCEPT this symbol is popped out and left.

The PDA must begin with the sequence

START

POP

HERE

PUSH $

The entire input string must be read before the machine can accept the word.

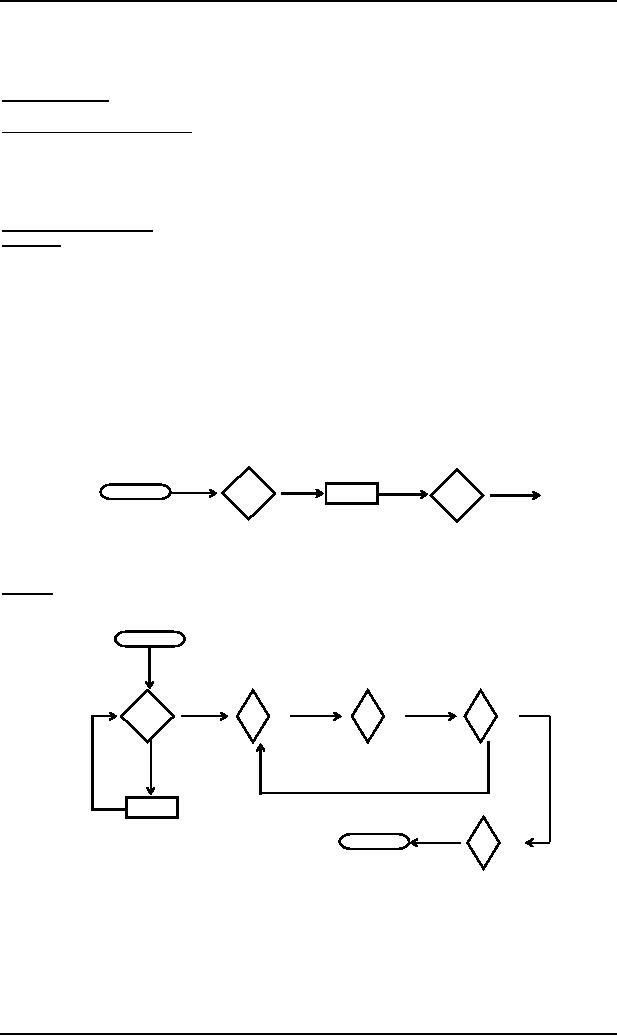
Example

Consider the following PDA accepting the language {a2nbn : n = 1,2,3, ...}

START

POP2

POP1

PUSH a

POP3

Which may be converted to

126

Theory of Automata

(CS402)

POP4

START

PUSH $

POP2

POP1

HERE

POP5

POP6

POP3

PUSH a

PUSH $

PUSH a

The above PDA accepts exactly the same language

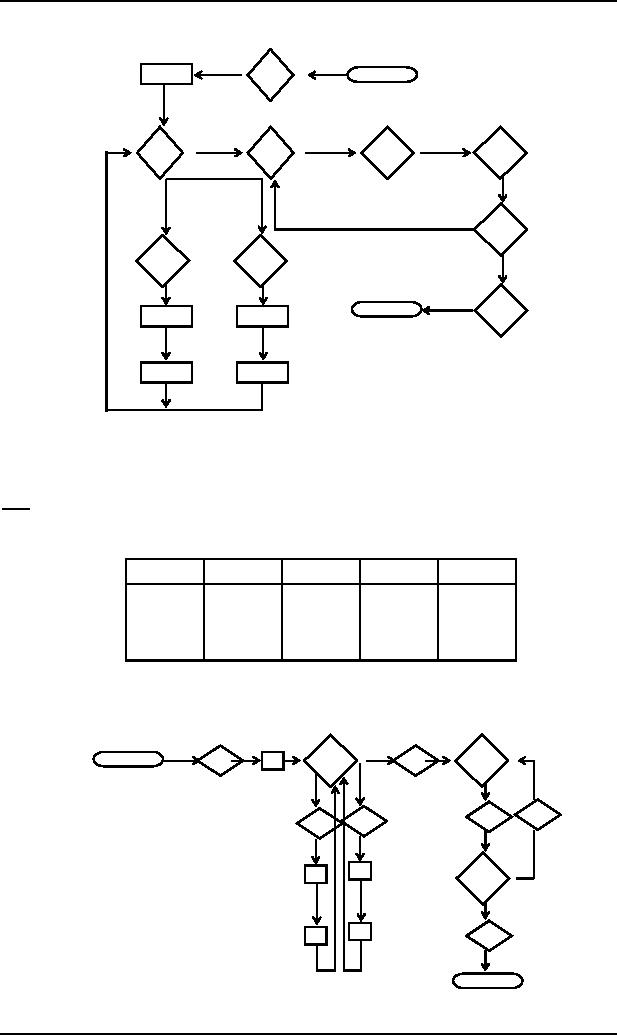
Note

It may be noted that any PDA which is in conversion form can be considered to be the collection of path

segments, where each path segment is of the following form

FROM

READ

POP

PUSH

START

READ

ONE or

Exactly

Any

or READ

or HERE

no input

one

string

STACK

onto the

or HERE

letter

character

STACK

START, READ, HERE and ACCEPT states are called the joints of the machine. Between two consecutive

joints on a path exactly one character is popped and any number of characters can be pushed.

The PDA which is in the conversion form can be supposed to be the set of joints with path segments in

between, similar to a TG

START

HERE

127

Theory of Automata

(CS402)

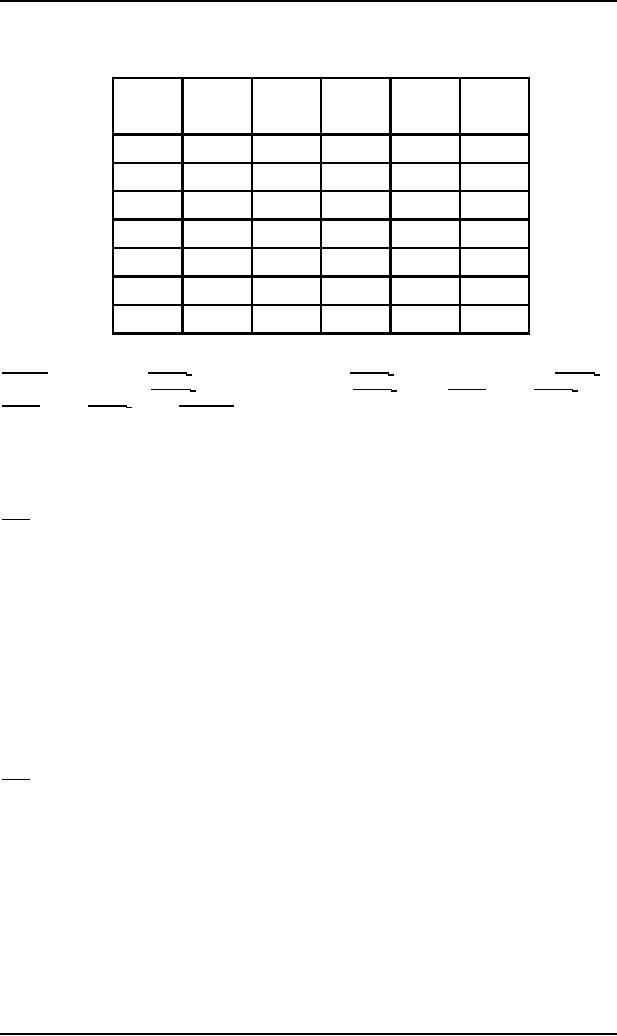
The above entire machine can be described as a list of all joint-to-joint path segments, called summary table.

The PDA converted to the conversion form has the following summary table

FROM

READ

POP

PUSH

ROW

Where

What

Number

START

HERE

HERE

Consider the word aaaabb. This word is accepted by the above PDA through the following path

START-POP4-PUSH$-READ1-POP6-PUSH $-PUSH a-READ1-POP5-PUSH a-PUSH a- READ1-

POP5-PUSH a-PUSH a-READ1-POP5-PUSH a-PUSH a-READ1-POP1- HERE-POP2-READ2-POP1-

HERE-POP2-READ2-POP3-ACCEPT.

The above path can also be expressed by the following path in terms of sequence of rows

Row1 Row2 Row3 Row3 Row3 Row4 Row5 Row6 Row5 Row7

It can be observed that the above path is not only joint-to-joint consistent but STACK consistent as well.

It may be noted that in FAs, paths correspond to strings of letters, while in PDAs, paths correspond to strings of

rows from the summary table.

Note

It may be noted that since the HERE state reads nothing from the TAPE, therefore L is kept in the READ what

column.

It may also be noted that the summary table contains all the information of the PDA which is in the pictorial

representation. Every path through the PDA is a sequence of rows of the summary table. However, not every

sequence of rows from the summary table represents a viable path, i.e. every sequence of rows may not be

STACK consistent.

It is very important to determine which sequences of rows do correspond to possible paths through the PDA,

because the paths are directly related to the language accepted, e.g. Row4 cannot be immediately followed by

Row6 because Row4 leaves in HERE, while Row6 begins in Read2. Some information must be kept about the

STACK before rows are concatenated.

To represent a path, a sequence of rows must be joint-consistent (the rows meet up end to end) and STACK-

consistent (when a row pops a character it should be there at the top of the STACK).

The next target is to define row language whose alphabet is Â = {Row1, Row2, ..., Row7} i.e. the alphabet

consists of the letters which are the names of the rows in the summary table.

Note

It may be noted that the words of the row language trace joint-to-joint and STACK consistent paths, which

shows that all the words of this language begin with Row1 and end in Row7. Consider the following row

sequence Row5 Row5 Row3 Row6

This is string of 4 letters, but not word of the row language because

It does not represent a path starting from START and ending in ACCEPT state.

It is not joint consistent.

It is not STACK consistent.

Before the CFG that generates the language accepted by the given PDA, is determined, the CFG that generates

the row language is to be determined. For this purpose new nonterminals are to be introduced that contain the

information needed to ensure joint and STACK consistency.

It is not needed to maintain any information about what characters are read from the TAPE.

128

Table of Contents: