Equivalent Regular Expressions

<< Regular Expression, Recursive definition of Regular Expression

Finite Automaton >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 4

Reading Material

Chapter 4, 5

Introduction to Computer Theory

Summary

Regular expression of EVEN-EVEN language, Difference between a* + b* and (a+b)*, Equivalent regular

expressions; sum, product and closure of regular expressions; regular languages, finite languages are regular,

introduction to finite automaton, definition of FA, transition table, transition diagram

An important example

The Language EVEN-EVEN

Language of strings, defined over Σ={a, b} having even number of a's and even number of b's. i.e.

EVEN-EVEN = {Λ, aa, bb, aaaa,aabb,abab, abba, baab, baba, bbaa, bbbb,...}, its regular expression can be

written as (aa+bb+(ab+ba)(aa+bb)*(ab+ba))*

Note

It is important to be clear about the difference of the following regular expressions

r1 = a*+b*

r2 = (a+b)*

Here r1 does not generate any string of concatenation of a and b, while r2 generates such strings.

Equivalent Regular Expressions

Definition

Two regular expressions are said to be equivalent if they generate the same language.

Example

Consider the following regular expressions

r1 = (a + b)* (aa + bb)

r2 = (a + b)*aa + ( a + b)*bb then both regular expressions define the language of strings ending in aa or bb.

Note

If r1 = (aa + bb) and r2 = ( a + b) then

r1+r2 = (aa + bb) + (a + b)

r1r2 = (aa + bb) (a + b)

= (aaa + aab + bba + bbb)

(r1)* = (aa + bb)*

Regular Languages

Definition

The language generated by any regular expression is called a regular language.

It is to be noted that if r1, r2 are regular expressions, corresponding to the languages L1 and L2

then the languages generated by r1+ r2, r1r2( or r2r1) and r1*( or r2*) are also regular

languages.

Note

It is to be noted that if L1 and L2 are expressed by r1and r2, respectively then the language expressed by

r1+ r2, is the language L1 + L2 or L1 « L2

r1r2, , is the language L1L2, of strings obtained by prefixing every string of L1 with every string of L2

r1*, is the language L1*, of strings obtained by concatenating the strings of L, including the null string.

Example

If r1 = (aa+bb) and r2 = (a+b) then the language of strings generated by r1+r2, is also a regular language,

expressed by (aa+bb) + (a+b)

If r1 = (aa+bb) and r2 = (a+b) then the language of strings generated by r1r2, is also a regular language, expressed

by (aa+bb)(a+b)

If r = (aa+bb) then the language of strings generated by r*, is also a regular language, expressed by (aa+bb)*

Theory of Automata

(CS402)

All finite languages are regular

Example

Consider the language L, defined over Σ = {a,b}, of strings of length 2, starting with a, then

L = {aa, ab}, may be expressed by the regular expression aa+ab. Hence L, by definition, is a regular language.

Note

It may be noted that if a language contains even thousand words, its RE may be expressed, placing ` + ' between

all the words.

Here the special structure of RE is not important.

Consider the language L = {aaa, aab, aba, abb, baa, bab, bba, bbb}, that may be expressed by a RE

aaa+aab+aba+abb+baa+bab+bba+bbb, which is equivalent to (a+b)(a+b)(a+b).

Introduction to Finite Automaton

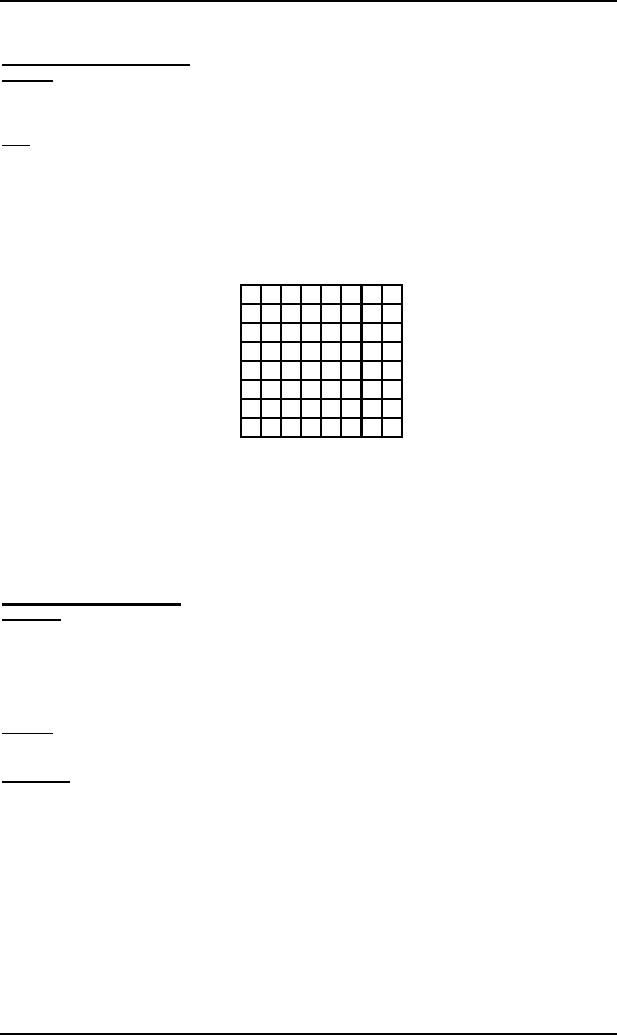
Consider the following game board that contains 64 boxes

There are some pieces of paper. Some are of white colour while others are of black colour. The number of

pieces of paper are 64 or less. The possible arrangements under which these pieces of paper can be placed in the

boxes, are finite. To start the game, one of the arrangements is supposed to be initial arrangement. There is a

pair of dice that can generate the numbers 2,3,4,...12 . For each number generated, a unique arrangement is

associated among the possible arrangements.

It shows that the total number of transition rules of arrangement are finite. One and more arrangements can be

supposed to be the winning arrangement. It can be observed that the winning of the game depends on the

sequence in which the numbers are generated. This structure of game can be considered to be a finite automaton.

Method 4 (Finite Automaton)

Definition

A Finite automaton (FA), is a collection of the followings

Finite number of states, having one initial and some (maybe none) final states.

Finite set of input letters (Σ) from which input strings are formed.

Finite set of transitions i.e. for each state and for each input letter there is a transition showing how to move

from one state to another.

Example

Σ = {a,b}

States: x, y, z where x is an initial state and z is final state.

Transitions:

At state x reading a, go to state z

At state x reading b, go to state y

At state y reading a, b go to state y

At state z reading a, b go to state z

These transitions can be expressed by the following table called transition table

Theory of Automata

(CS402)

Old States

New States

Reading a

Reading b

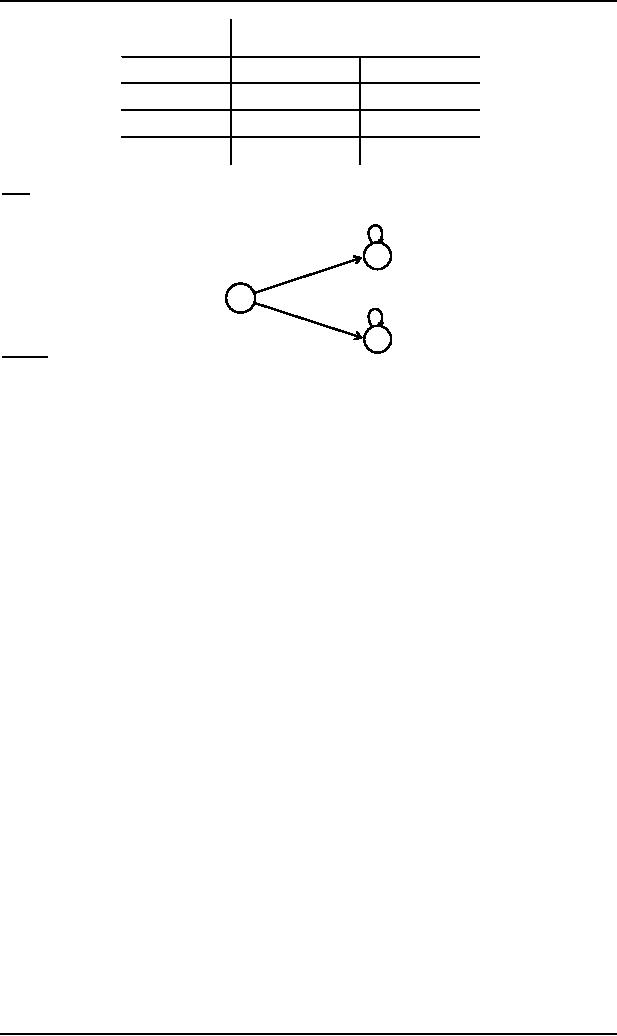
Note

It may be noted that the information of an FA, given in the previous table, can also be depicted by the following

diagram, called the transition diagram, of the given FA

a,b

Z+

Remark

The above transition diagram is an FA accepting the language of strings, defined over Σ = {a, b}, starting with

a. It may be noted that this language may be expressed by the regular expression a(a + b)*

Table of Contents: