ZeePedia

PDA corresponding to CFG

<< Nondeterministic PDA
Conversion form of PDA >>
img
Theory of Automata
(CS402)
Theory of Automata
Lecture N0. 39
Reading Material
Introduction to Computer Theory
Chapter 15
Summary
PDA corresponding to CFG, Examples of PDA corresponding to CFG
PDA corresponding to CFG
Theorem
Corresponding to any CFG there exists a PDA accepting the language generated by the CFG.
Since an algorithm has already been discussed to convert the CFG in CNF, so the PDA can be constructed
corresponding to the CFG. As the CFG in CNF generates all the nonnull words of the corresponding CFL, so
accepting the null string (if it is contained in the CFL), can be managed separately.
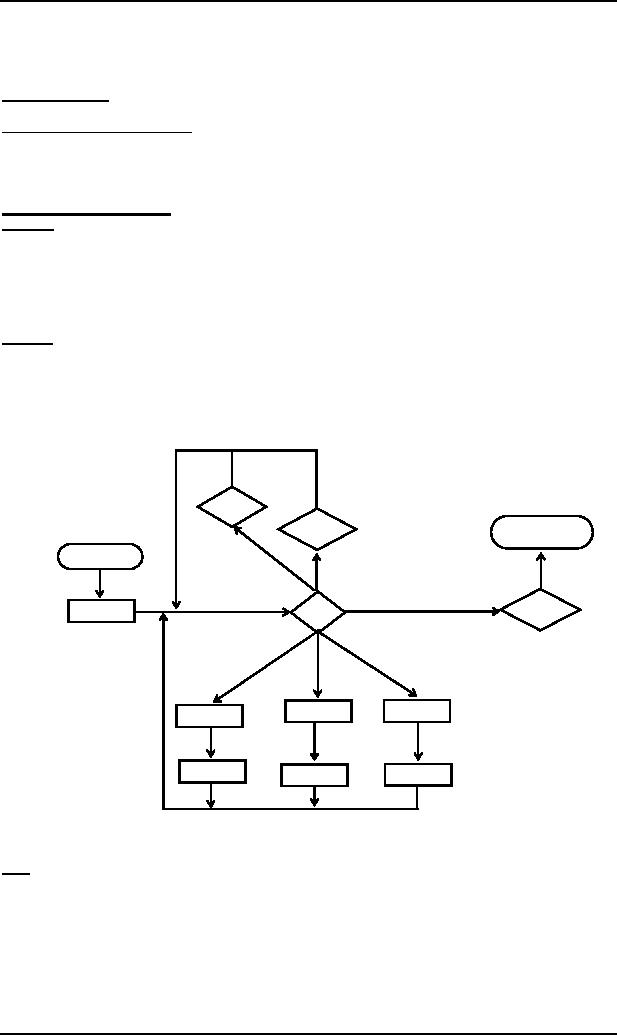
Example
Consider the following CFG which is in CNF and does not generate the null string
S � SB|AB
A � CC
B�b
C�a
The corresponding PDA will be
a
b
READ1
READ2
ACCEPT
START
C
B
READ3
PUSH S
POP
S
A
S
PUSH C
PUSH B
PUSH B
PUSH S
PUSH A
PUSH C
Here the STACK alphabet G= {S, A, B, C}, where the TAPE alphabet �={a, b}
Note: It may be noted that when the POP state is entered either a nonterminal is replaced by two nonterminals at
the top of the STACK accommodating a production, or a nonterminal is popped out from the top of the stack
and a READ state is entered to read a specified letter from the TAPE or else the machine crashes.
The choice of path taken at POP state to accommodate the word belonging to the CFL can be determined by the
left most derivation of the word. Consider the word aab with its left most derivation, as follows
119
img
Theory of Automata
(CS402)
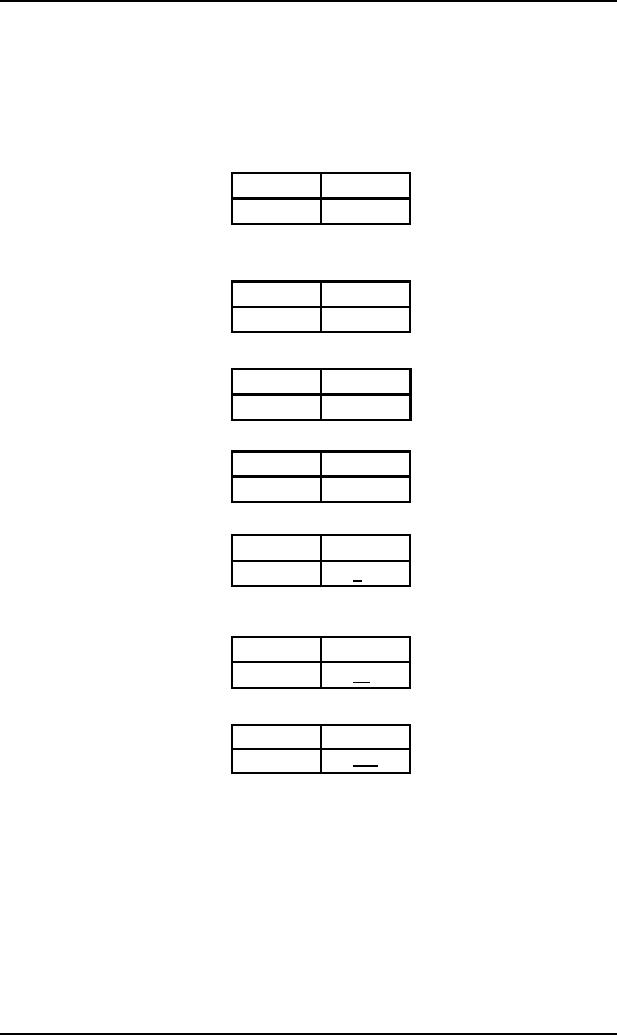
Working-String Generation
Production
Used
S fi AB
S � AB
step 1
fi CCB
A � CC
step 2
fi aCB
C�a
step 3
fi aaB
C�a
step 4
fi aab
B�b
step 5
First of all the START state is entered
STACK
TAPE
...
aab ...
The PUSH S state is entered
STACK
TAPE
aab ...
S
The POP state is entered and to accommodate the production S � AB, PUSH B and PUSH A states are entered.
STACK
TAPE
aab ...
AB
Then the POP state is entered and to accommodate the production A � CC, PUSH C, PUSH C states are entered
STACK
TAPE
CCB
aab
The POP state is entered and to accommodate the production C � a, READ1 is entered and the letter a is read
from the TAPE.
STACK
TAPE
CB
aab
The POP state is entered and to accommodate the production C � a, READ1 state is entered and the letter a is
read from the TAPE
STACK
TAPE
aab
B
The POP state is entered and to accommodate the production B � b, READ2 state is entered and the letter b is
read from the TAPE
STACK
TAPE
aab
D
The D shown in the STACK indicates that there are no nonterminals in the working string and D is read from the
STACK which leads to READ3 state where the D is read from the TAPE and the ACCEPT state is entered
which shows that the word aab is accepted by the PDA.
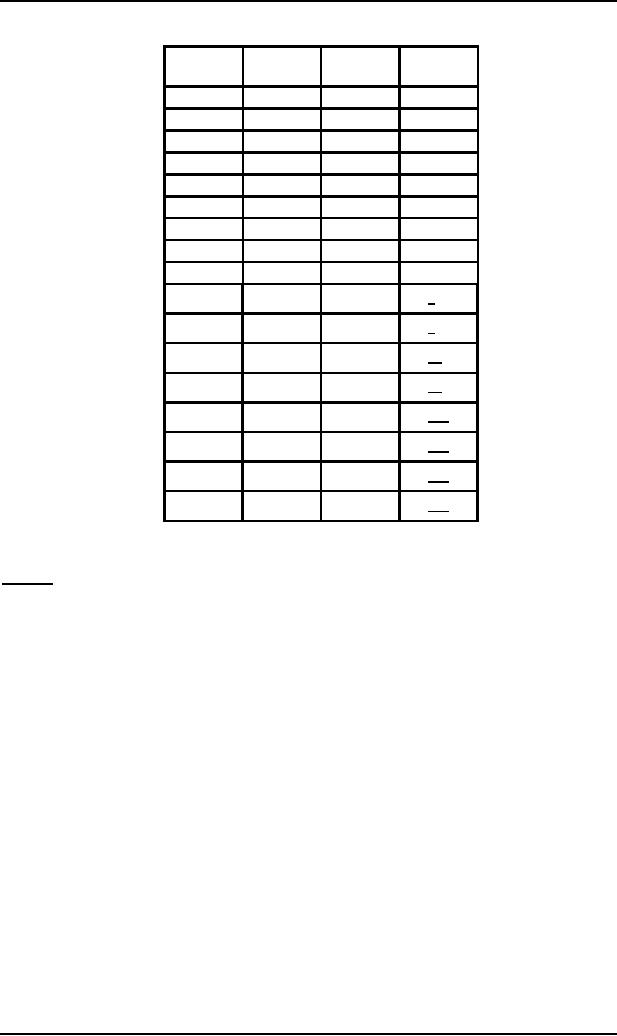
Following is the table showing all the observations discussed above, for the word aab
120
img
Theory of Automata
(CS402)
Left most
STATE
STACK
TAPE
derivation
D
START
aab
S
PUSH S
S
aab
D
POP
aab
aab
PUSH B
B
fiAB
PUSH A
AB
aab
POP
B
aab
PUSH C
CB
aab
fiCCB
PUSH C
CCB
aab
POP
CB
aab
fiaCB
READ1
CB
aab
POP
B
aab
fiaaB
READ1
B
aab
D
POP
aab
fiaab
D
READ2
aab
D
POP
aab
D
READ3
aab
D
ACCEPT
aab
Following is an example of building the PDA corresponding to the given CFG
Example
Consider the following CFG
S � XY
X � aX | bX |a
Y � Ya | Yb | a
First of all, converting the CFG to be in CNF, introduce the nonterminals A and B as
A�a
B�b
The following CFG is in CNF
S � XY
X � AX | BX |a
Y � YA | YB | a
A�a
B�b
121
img
Theory of Automata
(CS402)
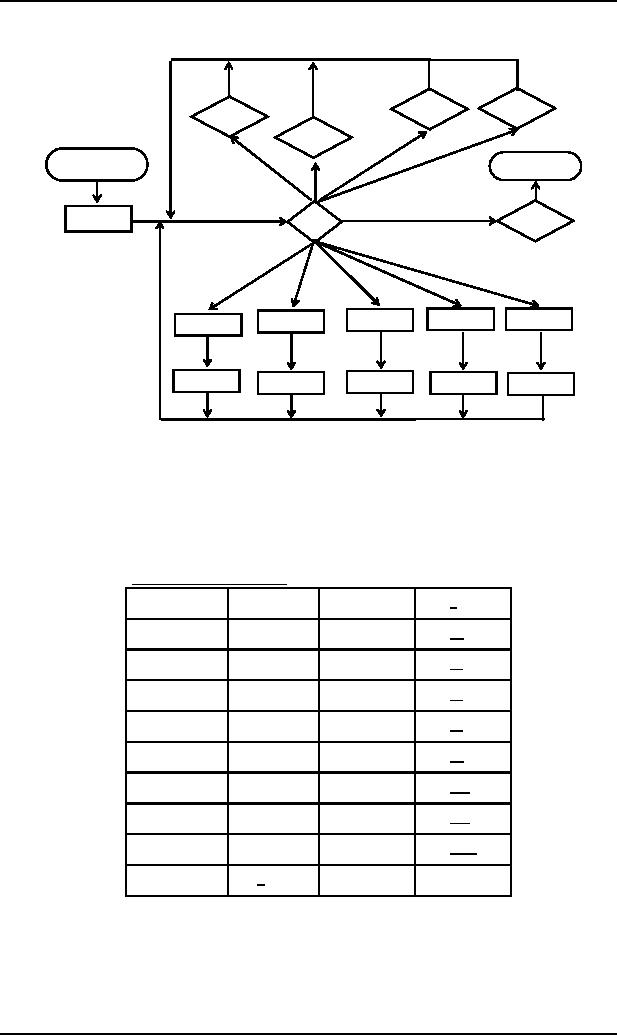
The PDA corresponding to the above CFG will be
a
b
a
a
READ3
READ4
READ1
READ2
B
A
START
ACCEPT
Y
X
PUSH S
READ5
POP
S
Y
X
X
Y
PUSH B
PUSH X
PUSH A
PUSH X
PUSH Y
PUSH X
PUSH B
PUSH A
PUSH Y
PUSH Y
The word aaab can be generated as
Working-String Generation
Production
Used
S fi XY
S � XY
step 1
fi AXY
X � AX
step 2
fi aXY
A�a
step 3
fi aaY
X�a
step 4
fi aaYB
Y � YB
step 5
fi aaaB
Y�a
step 6
fi aaab
B�b
step 7
STACK
TAPE
STACK
TAPE
(START)
aaab
(POP)
Y
aaab
(PUSH S) S
aaab
(READ1) Y
aaab
(POP)
(POP)
aaab
aabb
(PUSH Y) Y
aaab
(PUSH B) B
aabb
(PUSH X) XY
aaab
(PUSH Y) YB
aabb
aaab
(POP)
Y
aaab
(POP)
B
(PUSH X) XY
aaab
(READ2) B
aaab
(POP)
(PUSH A) AXY
aaab
aaab
(POP) XY
aaab
(READ4)
aaab
(POP)
(READ3) XY
aaab
122
Table of Contents:
  1. What does automata mean, Introduction to languages
  2. Kleene Star Closure, Recursive definition of languages
  3. Regular Expression, Recursive definition of Regular Expression
  4. Equivalent Regular Expressions
  5. Finite Automaton
  6. Equivalent FAs
  7. FA corresponding to finite languages
  8. Examples of TGs: accepting all strings
  9. Generalized Transition Graphs
  10. Nondeterminism, Kleene’s Theorem
  11. Proof(Kleene’s Theorem Part II)
  12. Kleene’s Theorem Part III
  13. Concatenation of FAs
  14. Closure of an FA
  15. Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
  16. NFA with Null String
  17. NFA and Kleene’s Theorem
  18. NFA corresponding to Concatenation of FAs
  19. Distinguishable strings and Indistinguishable strings
  20. Finite Automaton with output, Moore machine
  21. Mealy machine
  22. Equivalent machines
  23. Mealy machines in terms of sequential circuit
  24. Regular languages, Complement of a language
  25. Nonregular languages
  26. Pumping Lemma
  27. Pumping Lemma version II
  28. Pseudo theorem
  29. Decidability
  30. finiteness of a language
  31. Context Free Grammar (CFG), CFG terminologies
  32. Trees
  33. Polish Notation (o-o-o)
  34. Total language tree, Regular Grammar
  35. Null Production
  36. Chomsky Normal Form (CNF)
  37. A new format for FAs
  38. Nondeterministic PDA
  39. PDA corresponding to CFG
  40. Conversion form of PDA
  41. Conversion Form, Joints of the machine
  42. Row language, Nonterminals
  43. Non-Context-Free language, Pumping lemma for CFLs
  44. Decidablity, Parsing Techniques
  45. Turing machine