 |
A new format for FAs |
| << Chomsky Normal Form (CNF) |
| Nondeterministic PDA >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 37
Reading
Material
Introduction
to Computer Theory
Chapter
14
Summary
New
format for FAs, input
TAPE, START, ACCEPT , REJECT,
READ states Examples of New
Format of FA,
PUSH Down
STACK , PUSH and POP,
Example of PDA
A new
format for FAs
A class
of machines (FAs) has been
discussed accepting the
regular language i.e.
corresponding to a
regular
language
there is a machine in this
class, accepting that
language and corresponding to a machine
of this class
there is
a regular language accepted by
this machine. It has also
been discussed that there is
a CFG
corresponding to
regular language and CFGs
also define some nonregular
languages, as well
There is
a question whether there is a class of
machines accepting the CFLs?
The answer is yes. The
new
machines
which are to be defined are
more powerful and can be
constructed with the help of
FAs with new
format.
To define
the new format of an FA,
the following are to be
defined
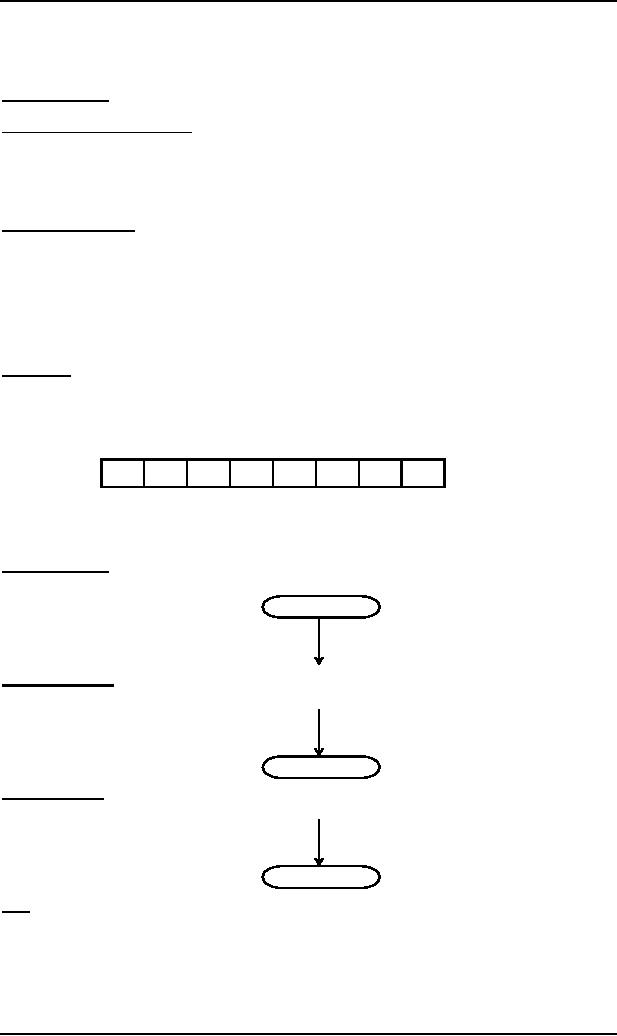
Input
TAPE
The part
of an FA, where the input string is
placed before it is run, is called the
input TAPE.
The
input TAPE is supposed to
accommodate all possible
strings. The input TAPE is
partitioned with cells,
so
that
each letter of the input string
can be placed in each cell.
The input string abbaa is shown in
the following
input
TAPE.
Cell i
Cell ii Cell iii
a
b
b
a
a
.
The
character indicates a blank in
the TAPE. The input
string is read from the
TAPE starting from the cell
(i).
It is
assumed that when first
is read, the rest of
the TAPE is supposed to be
blank.
The
START state
This
state is like initial state
of an FA and is represented by
START
An ACCEPT
state
This
state is like a final state
of an FA and is expressed by
ACCEPT
A REJECT
state
This
state is like dead-end non
final state and is expressed
by
REJECT
Note: It
may be noted that the
ACCEPT and REJECT states
are called the halt
states.
110
Theory of
Automata
(CS402)
A READ
state
This
state is to read an input letter
and lead to some other
state. The READ state is
expressed by
a
b
READ
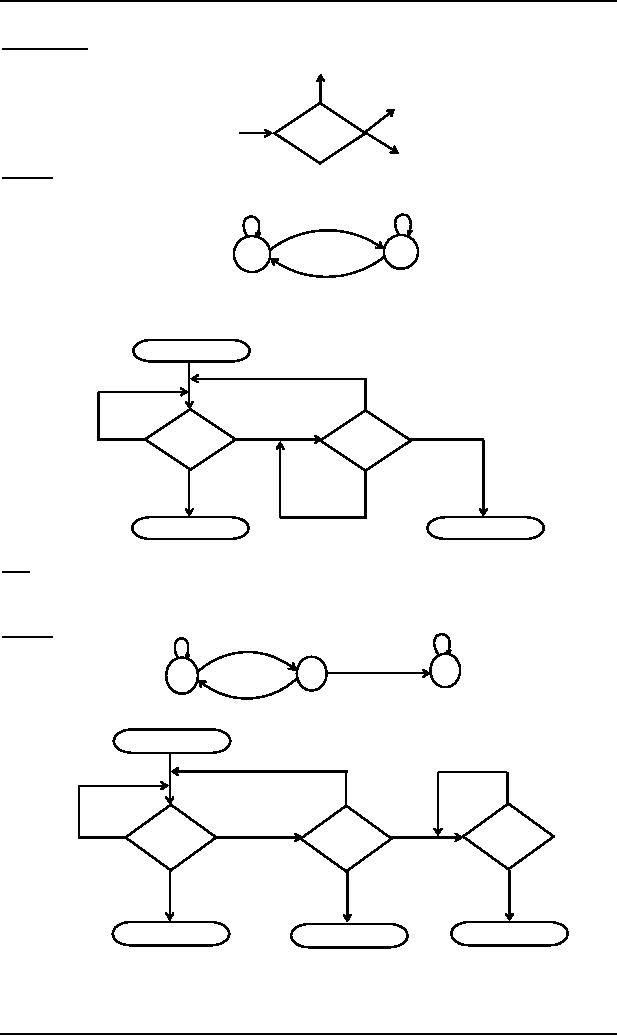
Example
Before
some other states are
defined consider the
following example of an FA along with
its new format
a
b
a
y+
x-
b
Obviously
the above FA accepts the
language of strings, expressed by
(a+b)*a. Following is the
new format of
the
above FA
START
b
a
READ
READ
b
a
REJECT
ACCEPT
Note
The
edge should not be confused with
Y-labeled
edge. The -edges start
only from READ boxes
and lead to
halt
states.
a,b
Example
a
b
b
+
1
+
-
1
a
The
above FA accepts the
language expressed by
(a+b)*bb(a+b)*
START
a
a,b
a
b
b
READ
READ
READ
REJECT
ACCEPT
REJECT
111
Theory of
Automata
(CS402)
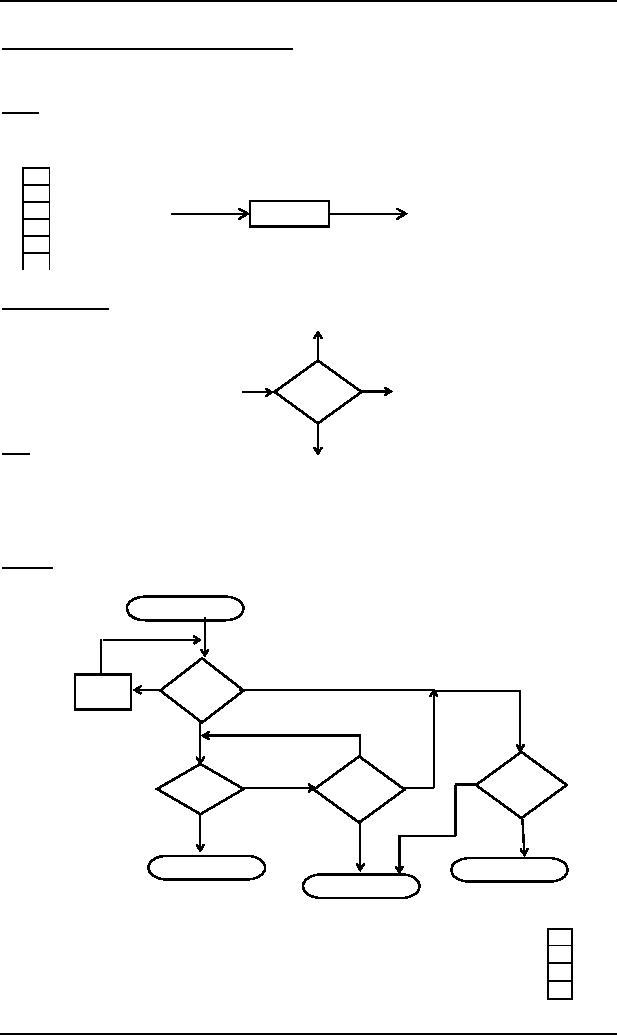
PUSHDOWN
STACK or PUSHDOWN
STORE
PUSHDOWN
STACK is a place where the
input letters can be placed
until these letters are
refered again. It can
store as
many letters as one can in a
long column.
Initially
the STACK is supposed to be
empty i.e.
each of
its storage location contains a
blank.
PUSH
A PUSH operator
adds a new letter at the top of
STACK, for e.g.
if
the letters a, b, c and d
are pushed to the
STACK
that was initially blank,
the STACK can be shown
as
STACK
The PUSH
state is expressed by
d
c
b
PUSH
a
a
When a
letter is pushed, it replaces the
existing letter and pushes it one
position below.
�
POP
and STACK
POP is an
operation that takes out a letter from
the top of the STACK. The
rest of the letters are
moved one
location
up. POP state is expressed
as
b
a
POP
Note
It may be
noted that popping an empty
STACK is like reading an empty TAPE,
i.e.
popping a
blank character .
It may
also be noted that when
the new format of an FA
contains PUSH and POP
states, it is called
PUSHDOWN
Automata or PDAs. It may be observed that
if the PUSHDOWN STACK (the memory
structure)
is added
to an FA then its language recognizing
capabilities are increased considerably.
Following is an example
of
PDA
Example
Consider
the following PDA
START
a
READ1
PUSH
a
b
b
a
READ2
POP2
POP1
b,
a,b
a
REJECT
ACCEPT
REJECT
STACK
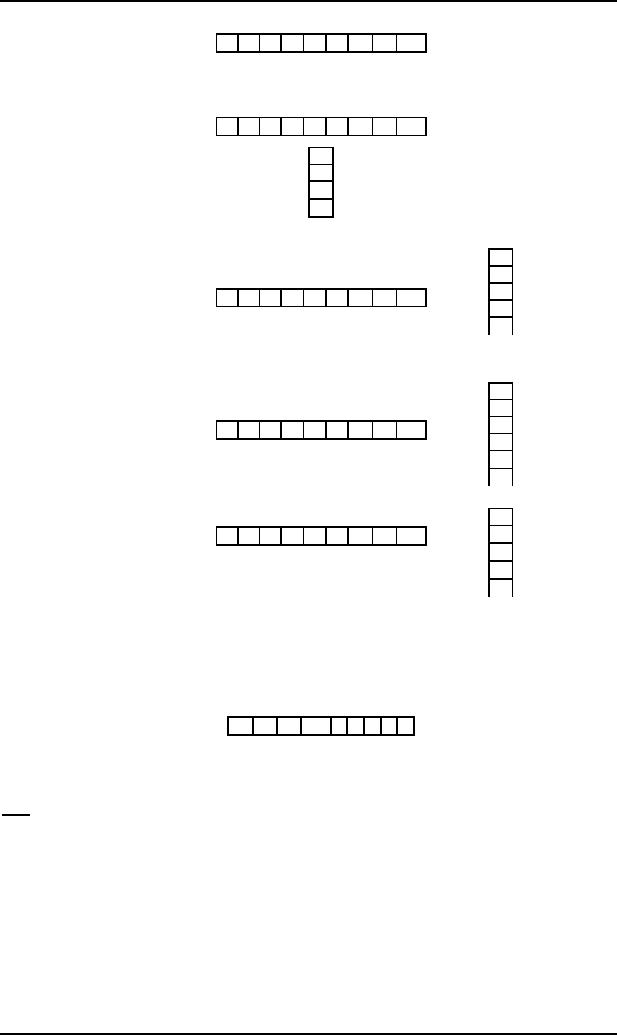
The
string aaabbb is to be run on this
machine. Before the string
is processed,
D the
string is
supposed to be placed on the
TAPE and the STACK is
supposed to
be
empty as
shown below
112
Theory of
Automata
(CS402)
D
D
∫
a
a
a
b
b
b
Reading
first a from the TAPE we
move from READ1State to PUSH a state, it
causes the letter a deleted
from
the
TAPE and added to the
top of the STACK, as shown
below
TAPE
a a a b
b b D D
∫
/
STACK
a
Reading
next two a's successively, will
delete further two a's
from
STACKthe
TAPE
and
a
add
these letters to the top of
the STACK, as shown
below
a
a
TAPE
a a a b
b b D D
∫
///
�
Then
reading the next letter which is b
from the TAPE will
lead to the POP1 state. The top letter at the
STACK
STACK
STACK is shown
is a,
which is popped out and READ2 state is entered. Situation of
TAPE and
a
below
a
a
TAPE
a a a b
b b D D
∫
////
�
Reading
the next two b's
successively will delete two b's
from the TAPE, will lead to
the
STACK
POP1 state and these
b's will be removed from the
STACK as shown
below
D
D
∫
a
a
a
b
b
b
TAPE
/
/
/
/
/
/
�
Now
there is only blank
character left, to be read
from the TAPE, which
leads to POP2 state. While the
only
blank
characters is left in the
STACK to be popped out and
the ACCEPT state is entered,
which shows that
the
string
aaabbb is accepted by this
PDA. It may be observed that
the above PDA accepts
the language
{anbn: n
= 0,1,2, ... }.
Since
the null string is like a
blank character, so to determine how
the null string is accepted, it
can be placed in
the
TAPE as shown below
TAPE
D D D
∫
Reading at
state READ1 leads to POP2 state and POP2 state contains only ,
hence it leads to ACCEPT
state
and
the null string is
accepted.
Note: The
process of running the string
aaabbb can also be expressed
in the table given in the
next lecture.
113
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine