ZeePedia

Chomsky Normal Form (CNF)

<< Null Production
A new format for FAs >>
img
Theory of Automata
(CS402)
Theory of Automata
Lecture N0. 36
Reading Material
Introduction to Computer Theory
Chapter 13,14
Summary
Chomsky Normal Form, Theorem regarding CNF, examples of converting CFG to be in CNF, Example of an
FA corresponding to Regular CFG, Left most and Right most derivations, New format of FAs.
Chomsky Normal Form (CNF)
If a CFG has only productions of the form
nonterminal Æ string of two nonterminals
or
nonterminal Æ one terminal
then the CFG is said to be in Chomsky Normal Form (CNF).
Note
It is to be noted that any CFG can be converted to be in CNF, if the null productions and unit productions are
removed. Also if a CFG contains nullable productions as well, then the corresponding new production are also
to be added. Which leads the following theorem
Theorem
All NONNULL words of the CFL can be generated by the corresponding CFG which is in CNF i.e. the
grammar in CNF will generate the same language except the null string.
Following is an example showing that a CFG in CNF generates all nonnull words of corresponding CFL.
Example
Consider the following CFG
S Æ aSa|bSb|a|b|aa|bb
To convert the above CFG to be in CNF, introduce the new productions as
A Æ a, B Æ b, then the new CFG will be
S Æ ASA|BSB|AA|BB|a|b
AÆa
BÆb
Introduce nonterminals R1 and R2 so that
S Æ AR1|BR2|AA|BB|a|b
R1 Æ SA
R2 Æ SB
AÆa
BÆb
which is in CNF.
It may be observed that the above CFG which is in CNF generates the NONNULLPALINDROME, which does
not contain the null string.
Example
Consider the following CFG
S Æ ABAB
A Æ a|L
B Æ b|L
Here S Æ ABAB is nullable production and A Æ L, B Æ L are null productions. Removing the null productions
A Æ L and B Æ L, and introducing the new productions as
S Æ BAB|AAB|ABB|ABA|AA|AB|BA|BB|A|B
Now S Æ A|B are unit productions to be eliminated as shown below
S Æ A gives S Æ a (using A Æ a)
S Æ B gives S Æ b (using B Æ b)
Thus the new resultant CFG takes the form
107
img
Theory of Automata
(CS402)
S Æ BAB|AAB|ABB|ABA|AA|AB|BA|BB|a|b, A Æ a, B Æ b.
Introduce the nonterminal C where C Æ AB, so that
S Æ BAB|AAB|ABB|ABA|AA|AB|BA|BB|a|b
S Æ BC|AC|CB|CA|AA|C|BA|BB|a|b
AÆa
BÆb
C Æ AB
is the CFG in CNF.
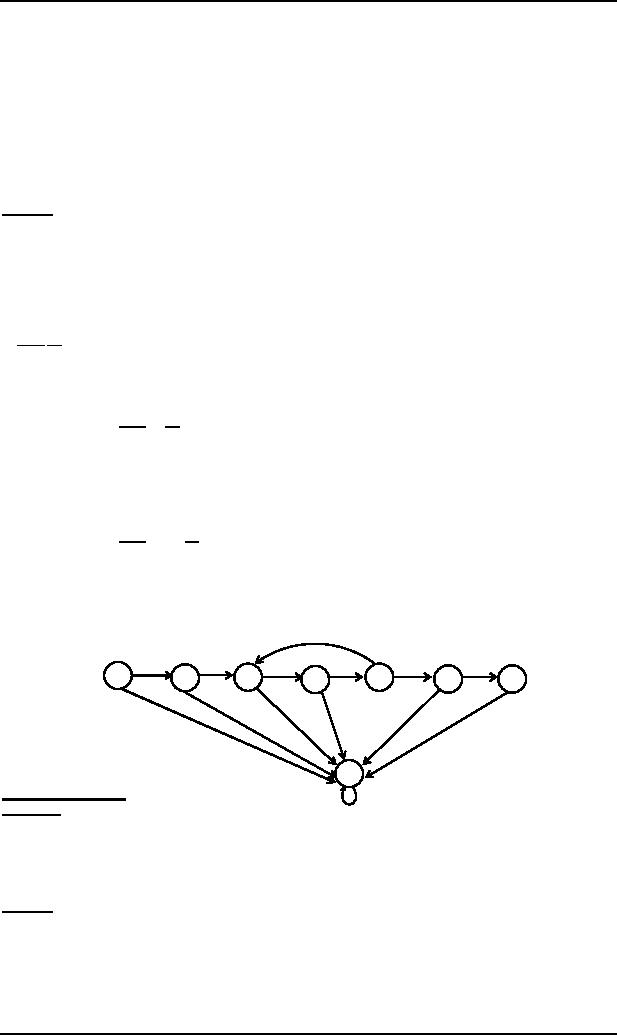
Example
To construct an FA that accepts the grammar
SÆabA
AÆbaB
BÆaA|bb
The language can be identified by the three words generated as follows
fi abA
S
fi abbaB
(using AÆbaB)
(using BÆbb)
fi abba bb
fi abA
S
fi abbaB
(using AÆbaB)
fi abbaaA
(using BÆ aA)
fi abbaabaB
(using AÆ baB)
fi abbaababb
(using BÆ bb)
fi abA
S
fi abbaB
(using AÆbaB)
fi abbaaA
(using BÆ aA)
fi abbaabaB
(using AÆ baB)
fi abbaabaaA
(using BÆ aA)
fi abbaabaabaB
(using AÆ baB)
fi abbaabaababb
(using BÆ bb)
which shows that corresponding language has RE abba(aba)*bb. Thus the FA accepting the given CFG may be
a
S-
A
B
+
a
b
b
a
b
b
a
a
b
b
a
a,b
Left most derivation
a,b
Definition
The derivation of a word w, generated by a CFG, such that at each step, a production is applied to the left most
nonterminal in the working string, is said to be left most derivation.
It is to be noted that the nonterminal that occurs first from the left in the working string, is said to be left most
nonterminal.
Example
Consider the following CFG
SÆXY
X Æ XX|a
YÆYY|b
then following are the two left most derivations of aaabb
108
img
Theory of Automata
(CS402)
fi XY
S fi XY
S
fi XXY
fi XXY
fi aXY
fi XXXY
fi aXXY
fi aXXY
fi aaXY
fi aaXY
fi aaaY
fi aaaY
fi aaaYY
fi aaaYY
fi aaabY
fi aaabY
= aaabb
= aaabb
Theorem
Any word that can be generated by a certain CFG has also a left most derivation.
It is to be noted that the above theorem can be stated for right most derivation as well.
Example
Consider the following CFG
SÆYX
X Æ XX|b
YÆYY|a
Following are the left most and right most derivations of abbbb
S fi YX
fi YX
S
fi aX
fi YXX
fi aXX
fi YXb
fi abX
fi YXXb
fi abXX
fi YXbb
fi abbX
fi YXXbb
fi abbXX
fi YXbbb
fi abbbX
fi Ybbbb
= abbbb
= abbbb
A new format for FAs
A class of machines (FAs) has been discussed accepting the regular language i.e. corresponding to a regular
language there is a machine in this class, accepting that language and corresponding to a machine of this class
there is a regular language accepted by this machine. It has also been discussed that there is a CFG
corresponding to regular language and CFGs also define some nonregular languages, as well
There is a question whether there is a class of machines accepting the CFLs? The answer is yes. The new
machines which are to be defined are more powerful and can be constructed with the help of FAs with new
format.
To define the new format of an FA, some terms are defined in the next lecture.
109
Table of Contents:
  1. What does automata mean, Introduction to languages
  2. Kleene Star Closure, Recursive definition of languages
  3. Regular Expression, Recursive definition of Regular Expression
  4. Equivalent Regular Expressions
  5. Finite Automaton
  6. Equivalent FAs
  7. FA corresponding to finite languages
  8. Examples of TGs: accepting all strings
  9. Generalized Transition Graphs
  10. Nondeterminism, Kleene’s Theorem
  11. Proof(Kleene’s Theorem Part II)
  12. Kleene’s Theorem Part III
  13. Concatenation of FAs
  14. Closure of an FA
  15. Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
  16. NFA with Null String
  17. NFA and Kleene’s Theorem
  18. NFA corresponding to Concatenation of FAs
  19. Distinguishable strings and Indistinguishable strings
  20. Finite Automaton with output, Moore machine
  21. Mealy machine
  22. Equivalent machines
  23. Mealy machines in terms of sequential circuit
  24. Regular languages, Complement of a language
  25. Nonregular languages
  26. Pumping Lemma
  27. Pumping Lemma version II
  28. Pseudo theorem
  29. Decidability
  30. finiteness of a language
  31. Context Free Grammar (CFG), CFG terminologies
  32. Trees
  33. Polish Notation (o-o-o)
  34. Total language tree, Regular Grammar
  35. Null Production
  36. Chomsky Normal Form (CNF)
  37. A new format for FAs
  38. Nondeterministic PDA
  39. PDA corresponding to CFG
  40. Conversion form of PDA
  41. Conversion Form, Joints of the machine
  42. Row language, Nonterminals
  43. Non-Context-Free language, Pumping lemma for CFLs
  44. Decidablity, Parsing Techniques
  45. Turing machine