 |
Polish Notation (o-o-o) |
| << Trees |
| Total language tree, Regular Grammar >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 33
Reading
Material
Introduction
to Computer Theory
Chapter
12
Summary
Example
of trees, Polish Notation, examples,
Ambiguous CFG, example
Example
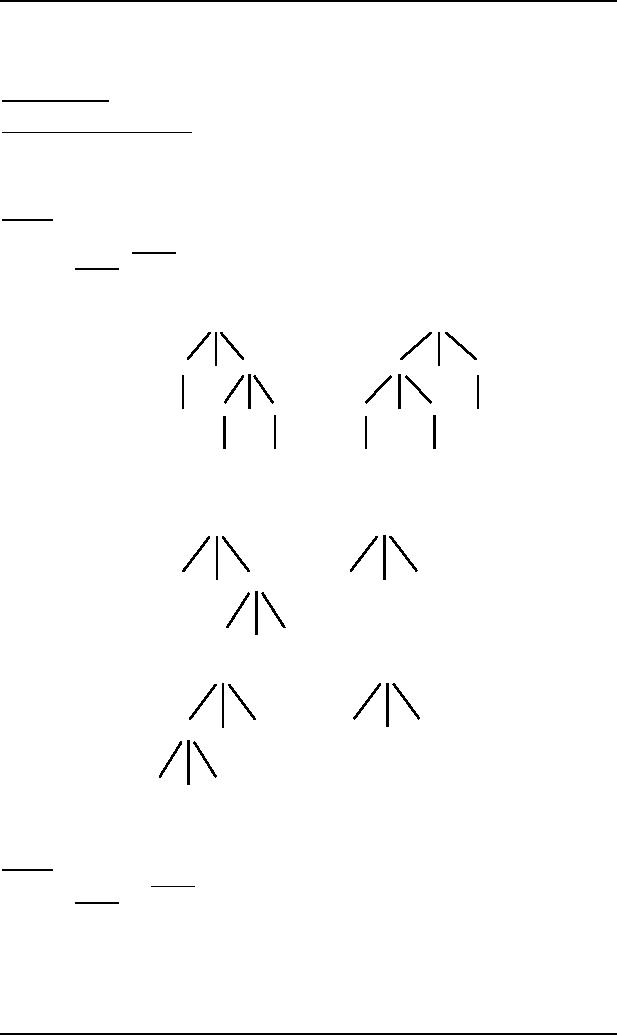
Consider
the following CFG
S � S+S|S*S|number
where S
and number are non-terminals and
the operators behave like
terminals.
The
above CFG creates ambiguity
as the expression 3+4*5 has
two possibilities (3+4)*5=35 and
3+(4*5)=23
which
can be expressed by the
following production
trees
S
S
S
S
S
S
(ii)
(i)
+
*
S
S
S
S
+
3
5
*
5
3
4
4
The
expressions can be calculated starting
from bottom to the top, replacing
each nonterminal by the
result of
calculation
e.g.
S
S
fi
fi
23
(i)
fi
S
3
3
20
+
+
5
4
*
S
S
Similarly
fi
fi 35
(ii)
fi
7
5
5
S
*
*
4
3
+
The
ambiguity that has been
observed in this example can be
removed with a change in the
CFG as discussed in
the
following example
Example
S � (S+S)|(S*S)|number
where S
and number are nonterminals, while (, *,
+, ) and the numbers are
terminals.
Here it
can be observed that
S fi (S+S)
fi (S+(S*S))
fi (3+(4*5))
= 23
S fi (S*S)
fi ((S+S)*S)
98
Theory of
Automata
(CS402)
fi ((3+4)*5)
= 35
Polish
Notation (o-o-o)
There is
another notation for arithmetic
expressions for the CFG, S�S+S|S*S|number.
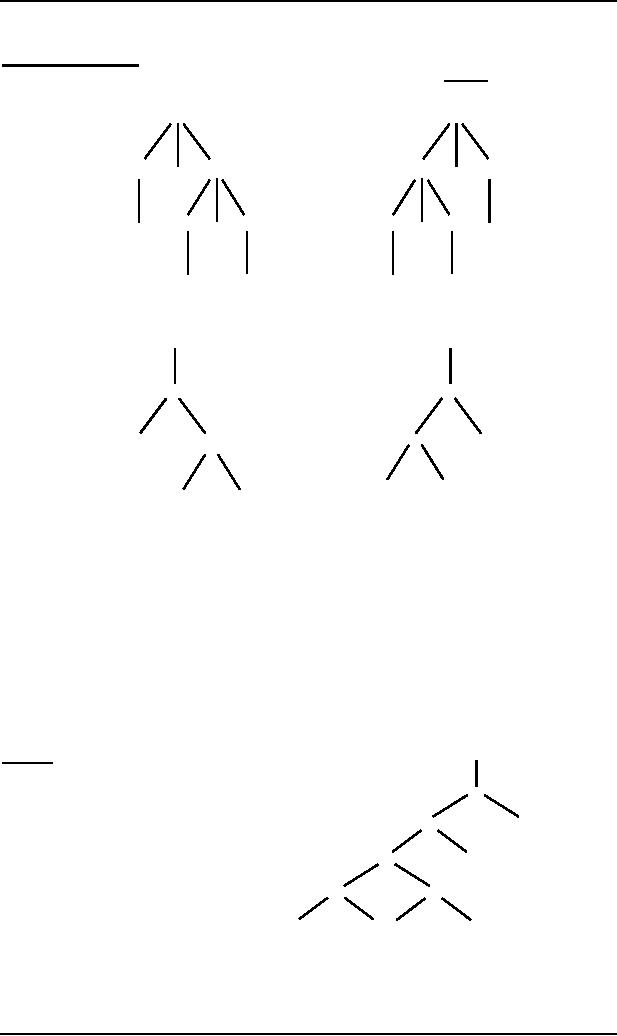
Consider the following
derivation
trees
S
S
S
S
S
S
(i)
(ii)
+
*
S
S
S
S
3
5
+
*
4
3
5
4
The
arithmetic expressions shown by the trees
(i) and (ii) can be
calculated from the
following trees,
respectively
S
S
+
*
+
3
5
(i)
(ii)
*
3
4
5
4
Here most
of the S's are eliminated.
The
branches are connected
directly with the operators.
Moreover, the operators +
and * are no longer
terminals
as these
are to be replaced by numbers
(results).
To write
the arithmetic expression, it is required
to traverse from the left
side of S and going onward
around the
tree.
The arithmetic expressions will be as
under
(i) + 3 *
4 5
(ii) * +3
4 5
The
above notation is called operator prefix
notation.
To evaluate
the strings of characters,
the first substring (from
the left) of the form
operator-operand-operand
(o-o-o)
is found and is replaced by
its calculation e.g.
+3*4 5 =
+3 20 = 23
*+3 4 5 =
* 7 5 = 35
It may be
noted that 4*5+3 is an infix
arithmetic expression, while an arithmetic
expression in (o-o-o) form is
a
prefix
arithmetic expression.
S
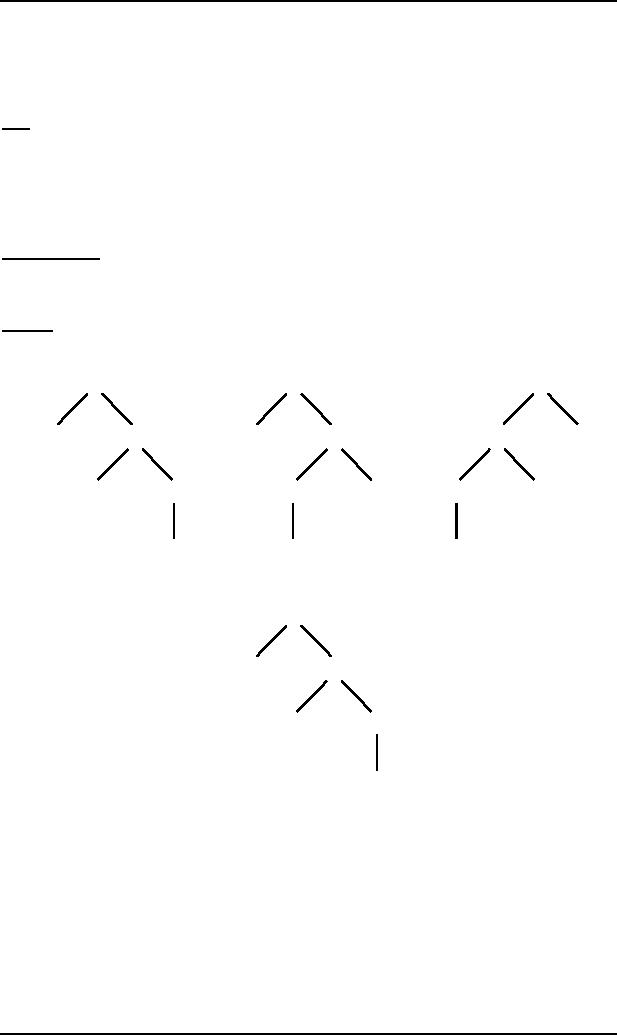
Example
To
calculate the arithmetic expression of
the following tree
*
+
6
5
*
+
+
1
3
4
2
99
Theory of
Automata
(CS402)
It can be
written as *+*+1 2+3 4 5 6
The
above arithmetic expression in (o-o-o)
form can be calculated
as
*+*+1 2+3
4 5 6 = *+*3+3 4 5 6
= *+*3 7
5 6 = *+21 5 6 = *26 6 =
156.
Note
The
previous prefix arithmetic expression
can be converted into the
following infix arithmetic expression
as
*+*+1
2+3 4 5 6
= *+*+1 2
(3+4) 5 6
=
*+*(1+2) (3+4) 5 6
=
*(((1+2)*(3+4)) + 5) 6
=
(((1+2)*(3+4)) + 5)*6
Ambiguous
CFG
The
CFG is said to be ambiguous if
there exists atleast one
word of it's language that
can be
generated
by the different production
trees.
Example:
Consider the following
CFG
S�aS|Sa|a
The
word aaa can be generated by
the following three
different trees
S
S
S
a
a
S
S
a
S
a
a
S
S
S
a
a
a
a
Thus the
above CFG is ambiguous,
while the CFG, S�aS|a is
not ambiguous as neither the word
aaa nor any
other
word can be derived from
more than one production
trees. The derivation tree
for aaa is as follows
S
a
S
a
S
a
100
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine