 |
Trees |
| << Context Free Grammar (CFG), CFG terminologies |
| Polish Notation (o-o-o) >> |

Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 32
Reading
Material
Introduction
to Computer Theory
Chapter
12
Summary
Examples
of CFL, EVEN-EVEN, EQUAL,
Language of strings containing
bbb,
PALINDROME,
{anbn},
Language of strings beginning
and ending in different
letters,
Parsing
tree, example
Example
� =
{a,b}
productions:
S � SS
S � XS
S�L
S � YSY
X � aa
X � bb
Y � ab
Y � ba
This
grammar generates EVEN-EVEN
language.
Example
� =
{a,b}
productions:
S � aB
S � bA
A�a
A � aS
A � bAA
B�b
B � bS
B � aBB
This
grammar generates the language
EQUAL(The language of strings,
with number of a's equal to number
of
b's).
Note
It is to be
noted that if the same
non-terminal have more than
one productions, it can be written in
single line
e.g.
S
�
aS, S
�
bS, S
� L
can be
written as S � aS|bS|L
It may
also be noted that the
productions S � SS|L always
defines the language which is
closed w.r.t.
concatenation
i.e.the
language expressed by RE of type
r*. It may also be noted
that the production S � SS
defines
the language expressed by r+.
Example
� =
{a,b}
productions:
S � YXY
Y � aY|bY|L
X � bbb
It can be
observed that, using prod.2, Y generates
L. Y
generates a. Y generates b. Y also
generates all the
combinations of a
and b. thus Y generates the
strings generated by (a+b). It may
also be observed that the
above
95

Theory of
Automata
(CS402)
CFG
generates the language
expressed by (a+b)*bbb(a+b)*. Following
are four words generated by
the given
CFG
fi YXY
S fi YXY
S
fi bYbbbaY
fi aYbbbL
fi bLbbbabY
fi abYbbb
fi bbbbabbY
fi abLbbb
fi bbbbabbaY
=
abbbb
fi bbbbabbaL
=
bbbbabba
S fi
fi YXY
YXY
S
fi
LbbbaY
fi bYbbbaY
fi
fi bLbbbaL
bbbabY
fi
=
bbbba
bbbabaY
fi
bbbabaL
=
bbbaba
Example
Consider
the following CFG
S � SS|XaXaX|L
X � bX|L
It can be
observed that, using prod.2, X generates
L. X
generates any number of b's.
Thus X generates the
strings
generated by b*. It may also
be observed that the above
CFG generates the language
expressed by
(b*ab*ab*)*.
Example
Consider
the following CFG
� =
{a,b}
productions:
S � aSa|bSb|a|b|L
The
above CFG generates the
language PALINDROME. It may be
noted that the
CFG
S � aSa|bSb|a|b
generates the language
NON-NULLPALINDROME.
Example
Consider
the following CFG
� =
{a,b}
productions:
S � aSb|ab|L
It can be
observed that the CFG
generates the language {anbn: n = 0,1,2,3, ...}. It
may also be noted that
the
language
{anbn:
n=1,2,3, ...} can be generated by
the CFG, S � aSb|ab
Example
Consider
the following CFG
S � aXb|bXa
X � aX|bX|L
The
above CFG generates the
language of strings, defined
over �={a,b},
beginning
and ending in
different
letters.
Trees
As in English
language any sentence can be
expressed by parse tree, so
any word generated by the
given CFG
can
also be expressed by the
parse tree, e.g.
consider
the following CFG
S � AA
A � AAA|bA|Ab|a
Obviously,
baab can be generated by the
above CFG. To express the
word baab as a parse tree,
start with S.
Replace S
by the string AA, of nonterminals,
drawing the downward lines
from S to each character of
this string
as
follows
S
A
A
96
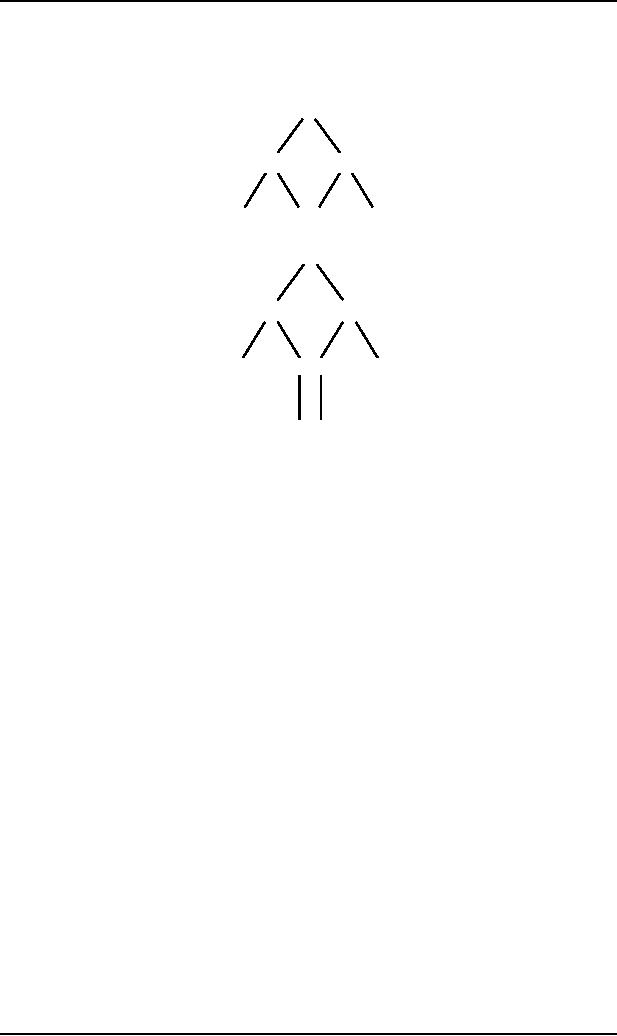
Theory of
Automata
(CS402)
Now let
the left A be replaced by bA
and the right one by Ab
then the tree will
be
S
A
A
AA
b
b
Replacing both
A's by a, the above tree
will be
S
A
A
AA
b
b
aa
Thus the
word baab is generated. The
above tree to generate the
word baab is called Syntax
tree or Generation
tree or
Derivation tree as
well.
97
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine