 |
Pseudo theorem |
| << Pumping Lemma version II |
| Decidability >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 28
Reading
Material
Chapter
10
Introduction
to Computer Theory
Summary
Examples
of Myhill Nerode theorem, Quotient of a
language, examples, Pseudo
theorem: Quotient of a
language
is regular, prefixes of a language,
example
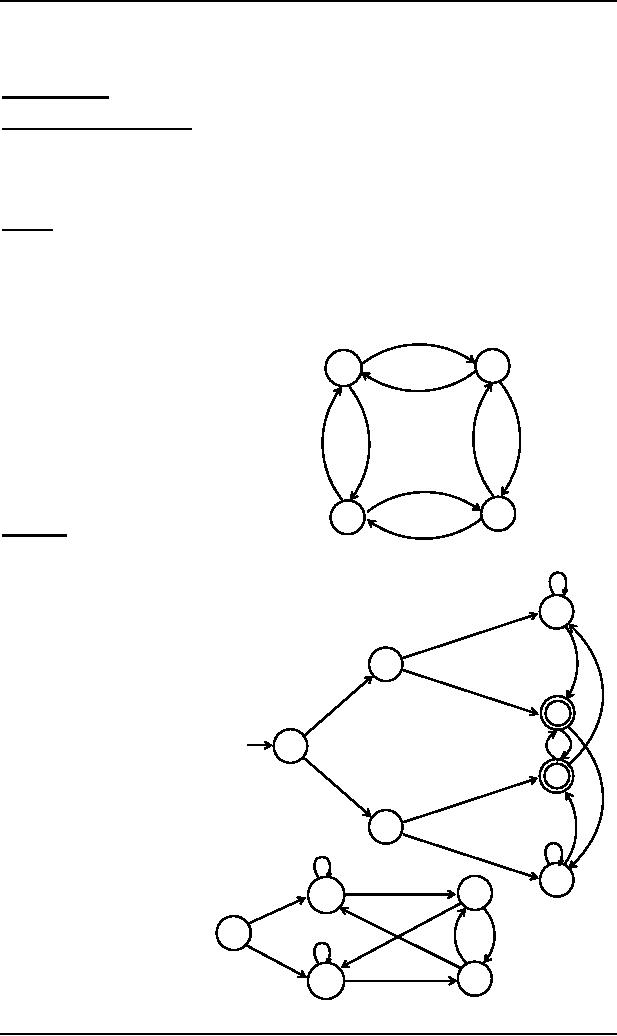
Example
Consider
the language L which is
EVEN-EVEN, defined over S = {a,b}.
It can be observed that L partitions S*
into
the following four
classes
C1 = set
of all strings with even
number of a's and odd number of
b's.
C2 = set
of all strings with odd number of
a's and odd number of
b's.
C3 = set
of all strings with odd number of
a's and even number of
b's.
C4 = set
of all strings with even
number of a's and even number of
b's. b
Since
there are finite many
classes generated
C1
C4�
by L, so L is
regular and hence following
is
b
an FA,
built with the help of C1, C2,
C3
and
C4, accepting L.
a
a
a
a
b
C2
C3
Example
b
Consider
the language L = {w OE {a,b}*:
length(w) ≥ 2, w ends
in either ab or ba}.
It can be
observed that L partitions S* into
the following seven
classes
a
C1 = set
containing only null string.
C2 = set
containing only letter a.
c4
C3 = set
containing only letter b.
a
C4 = set
of strings ending in
aa.
c2
C5 = set
of strings ending in
ab.
b
C6 = set
of strings ending in
ba.
b
a
a
C7 = set
of strings ending in
bb.
c5
Since
there are finite many
classes generated by
L, so L is
regular and hence FA
shown
b
c1
a
aside, is
built with the help
of C1,
C2, C3 , C4, C5 , C6 and
c6
b
a
C7,
accepting L
b
c3
a
b
b
a
c7
Following
is an FA equivalent to the above
FA
b
4+
2
a
b
a
1
a
b
b
b
a
5+
3
82

Theory of
Automata
(CS402)
Note It
can be noted, from the
above two FAs accepting
the same language, that if
the language L, partitions S*
into n
distinct classes, then L may
partition S* into
finite many distinct classes other
than n.
Quotient
of a language into
another
Remark
The theorem has been
proved to show under what conditions a
language is regular. It has also
been
proved
that the product of two
regular languages is regular.
The
question arises that whether
there exists a theorem
showing that quotient of regular
languages is regular.
There is
a problem in defining the quotient of
two regular languages. There
is an approach in defining
the
quotient of
regular languages i.e. the
language Q is said to be quotient
of two regular languages P and
R,
denoted
by Q=R/P if PQ=R.
It is to be
noted that this definition
does not determine a unique language e.g.
for P=Q=R expressed by a*
then
PQ=R
and so Q=R/P i.e. a*=a* /
a*. But for Q={Y}, P=R
expressed by a*, PQ=R is
still true which shows
that
Q={Y}=R/P
expressed by a* / a*
Similarly,
for the same P and R, Q
may be taken as {Y},{a},{aaaa},{aaaaaaaa},
... Thus there exist
infinite
many
choices for defining the
quotient language in this case of
one-letter alphabet.
Pseudo
theorem
Statement
For
three languages P,Q and R,
while PQ=R the language Q
must be regular if both P and R
are regular.
(Note: It
is to be noted that since
this theorem is not true, so
the theorem is called pseudo
theorem.)
Disproof
The
theorem can be disproved by contradiction
i.e. supposing that Q is
regular.
Let P=a*,
Q be the product of {anbn:n=0,1,2,...} and b* then
PQ=a*{anbn}b*=a*b*=R which shows
that R is
regular.
To
disproof this theorem, it is
sufficient to prove that Q is not
regualr. By definition, the words in Q
are of the
form
axby where x
y.
Let Q be regualr and hence
there exists an FA that
accepts Q. Suppose the number
of
states in
this machine be N. Now the
word aNbN is
also in Q and must be
accepted by this FA.
Since
the number of states in this
machine is N, there must be a
circuit in this machine to
run the substring aN.
Thus
while accepting the word
aNbN, the
machine looping the circuit
once again, can accept
the word
amore than
NbN, which is not in Q. Hence it is
impossible to find any FA that
accepts exactly the language
Q. Thus
Q is not
regular and hence the
theorem is disproved.
Prefixes
of a language in another
language
If two
languages R and Q are given,
then the language the
prefixes of Q in R denoted
by Pref(Q in
R) is
the set
of
strings of letters that, when
concatenated to the front of
some word in Q to produce
some word in R i.e.
Pref(Q in
R) = the set of all strings
p such that there exists
words q in Q and w in R such
that pq = w. Following
are
the examples in this
regard
Example
Let Q =
{aa,abaaabb,bbaaaaa,bbbbbbbbbb} and R =
{b,bbbb,bbbaaa,bbbaaaaa}
It can be
observed that aa and bbaaaaa
occur at the ending parts of
some words of R, hence these
words help in
defining
the language pref(Q in R).
Thus pref(Q in R) =
{b,bbba,bbbaaa}
Note: The
language of prefixes may be consisting of
word L, while there is also
a possibility that this
language
may not
contain any string (even not the
null string).
83
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine