 |
NFA corresponding to Concatenation of FAs |
| << NFA and Kleene’s Theorem |
| Distinguishable strings and Indistinguishable strings >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 18
Reading
Material
Introduction
to Computer Theory
Chapter
7
Summary
NFA
corresponding to union of FAs, example,
NFA corresponding to concatenation of
FAs, examples, NFA
corresponding to
closure of an FA,
example
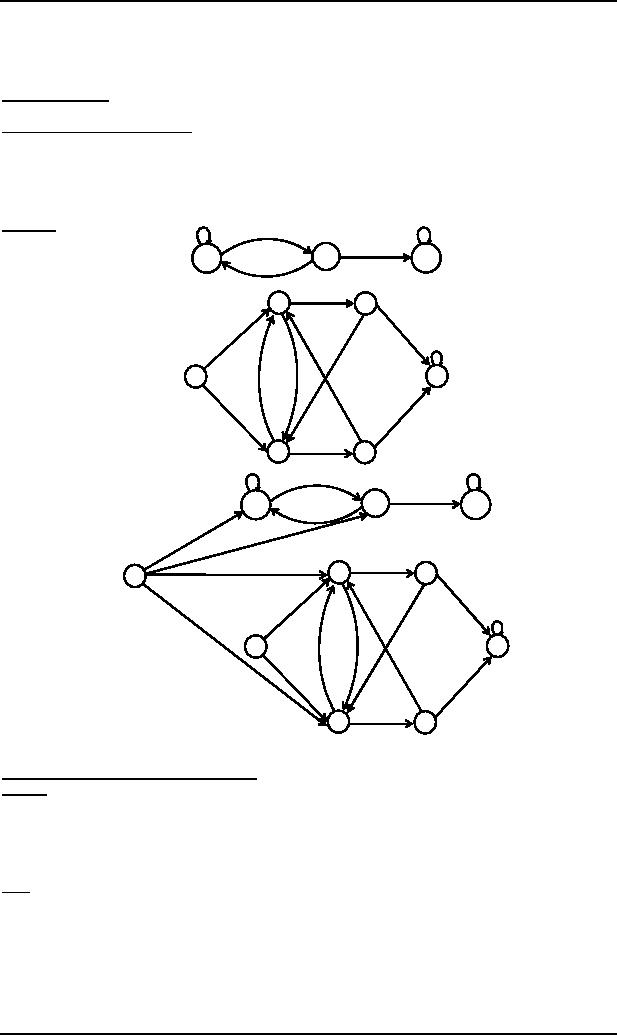
b
a,b
Example
a
a
q
FA1
p-
+
b
a
2
4
a
a
a,b
b
FA2
6+
1
a
b
b
a
b
b
3
5
3
a,b
b
a
a
q
p
+
b
b
a
a
a
2
4
-
a
a
a,b
b
b
1
6+
a
b
a
b
b
b
3
5
NFA
equivalent to FA1�FA2
NFA
corresponding to Concatenation of
FAs
Method
Introduce
additional transitions for
each letter connecting each final
state of the first FA with
the states of
second FA
that are connected with
the initial state of second
FA corresponding to each letter of the
alphabet.
Remove
the +ve sign of each of
final states of first FA and
ve sign of the initial
state of second FA. It
will
create
non-determinism at final states of first
FA and hence NFA, thus
obtained, will be the
required NFA.
Note
It may be
noted that if first FA
accepts the Null string then
every string accepted by second FA
must be accepted
by the
concatenation of FAs as well.
This situation will automatically be
accommodated using the
method
discussed
earlier. However if the
second FA accepts Null string,
then every string accepted by
first FA must be
accepted
by the required FA as well.
This target can be achieved
as, while introducing new
transitions at final
states of
first FA the +ve sign of
these states will not be
removed.
53
Theory of
Automata
(CS402)
Lastly if both
FAs accepts the Null string,
then the Null string must be
accepted by the required FA.
This
situation
will automatically be accommodated as the
second FA accepts the Null
string and hence the +ve
signs
of final
states of first FA will not
be removed.
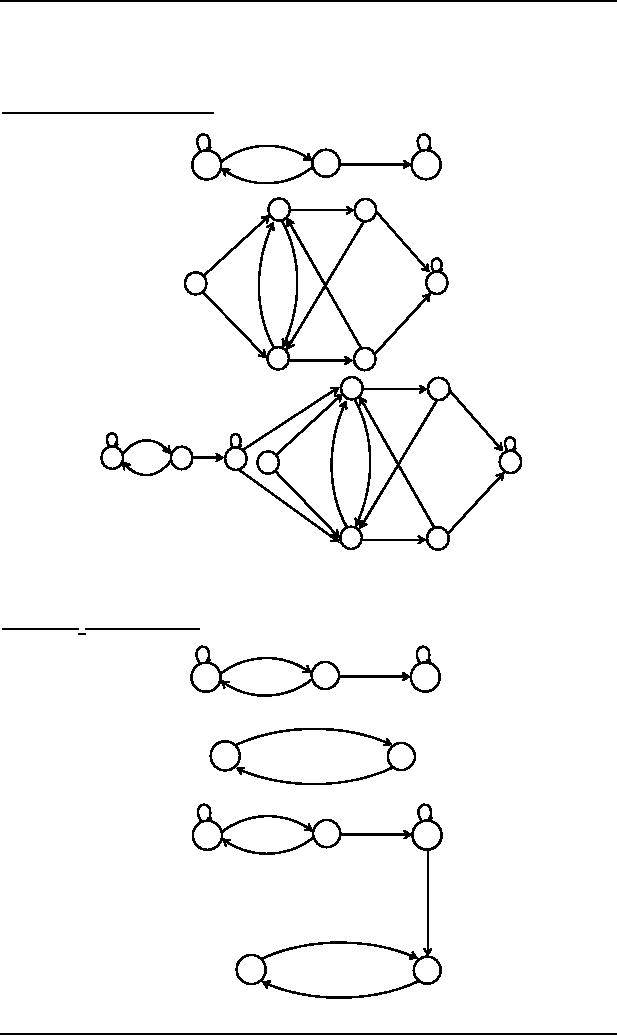
Example
(No FA accepts Null
string)
b
a,b
a
FA1
a
q
p-
r+
b
a
2
4
a
a
a,b
b
FA2
6+
1
a
b
b
a
b
b
3
5
3
a
2
4
a a
a
b
a,b
b
a,b
a
a
q
p-
r
a
6+
1
p
b
b
b
a
b
b
b
3
5
NFA
equivalent to FA1FA2
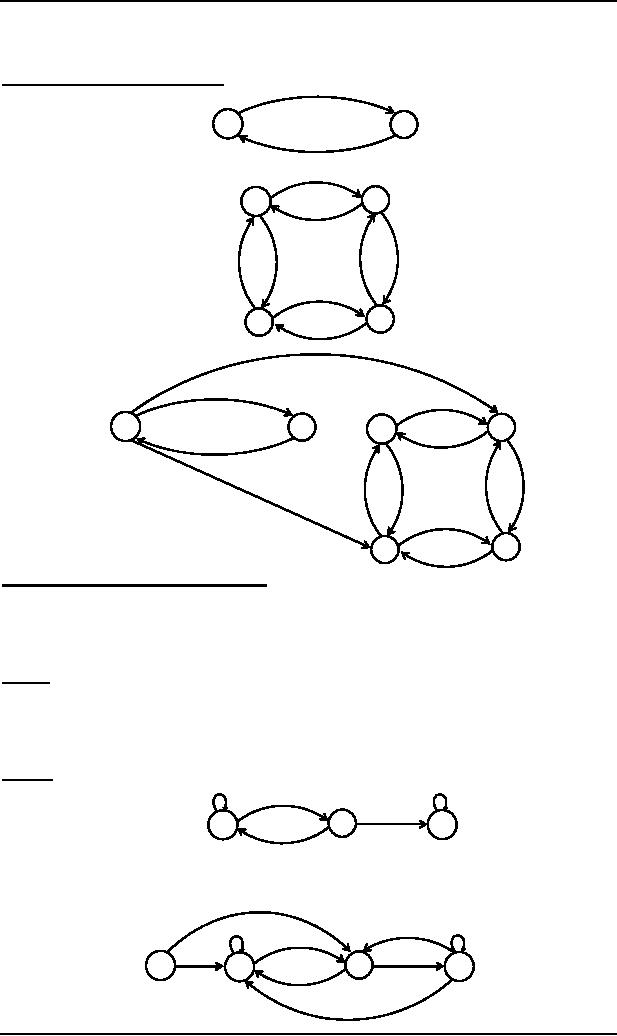
Example
(FA2 accepts Null
string)
b
a,b
a
a
q
p-
r+
b
FA1
a,
b
x�
y
FA2
a,
b
a,b
b
a
a
q
p-
r+
b
a,
b
a,
b
y
x+
a,
b
54
Theory of
Automata
(CS402)
NFA
equivalent to FA1FA2
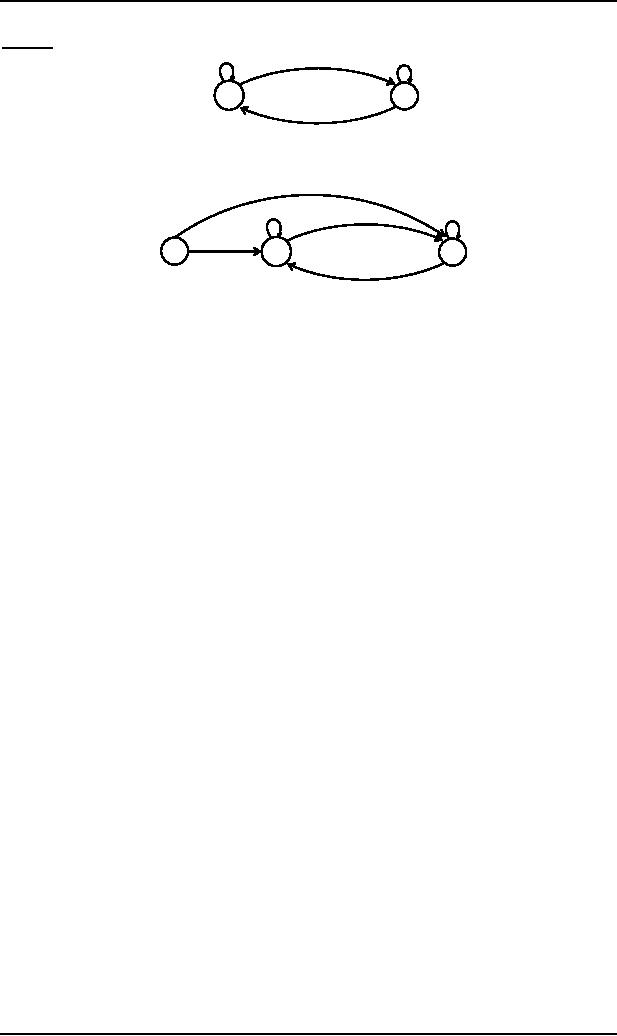
Example
(Both FAs accept Null
string)
a,
b
x�
y
FA1
a,
b
b
1�
3
b
a
a
a
a
FA2
b
4
2
b
b
a,
b
b
y
3
�
1+
b
a,
b
a
a
a
a
a
b
4
2
NFA
equivalent to FA1FA2
b
NFA
corresponding to the Closure of an
FA
Apparently, it
seems that since closure of
an FA accepts the Null string, so
the required NFA may be
obtained
considering
the initial state of given
FA to be final as well, but this
may allow the unwanted string to
be
accepted
as well. For example, an FA,
with two states, accepting
the language of strings,
defined over. S =
{a,
b},
ending in
a,
will accept all unwanted
strings, if the initial
state is supposed to be final as
well.
Method
Thus, to
accommodate this situation, introduce an
initial state which should be
final as well (so that
the Null
string is
accepted) and connect it
with the states originally
connected with the old
start state with the
same
transitions
as the old start state,
then remove the ve sign
of old start state.
Introduce new transitions,
for each
letter, at
each of the final states
(including new final state)
with those connected with
the old start
state.This
creates
non-determinism and hence results in
the required NFA.
Example
b
a,b
Consider
the following FA
a
a
2
1-
3+
b
It may be
observed that the FA* accepts only the
additional string which is the
Null string.
Considering
the state 1 to be final as
well, will allow the
unwanted strings be accepted as well.
Hence the
required
NFA is constructed introducing
the new initial state,
shown below.
a
a,b
a
b
a
b
a
�
2
1
3+
b
b
55
Theory of
Automata
(CS402)
Example
Consider
the following FA
b
a
a
1
2+
b
It may be
observed that the FA* accepts only the
additional string which is the
Null string
As observed in
the previous example the
required NFA can be
constructed only if the new
initial state is
introduced as shown
below.
a
b
a
a
b
�
1
2+
b
56
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine