Kleeneâ€™s Theorem Part III

<< Proof(Kleeneâ€™s Theorem Part II)

Concatenation of FAs >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 12

Reading Material

Chapter 7

Introduction to Computer Theory

Summary

Examples of writing REs to the corresponding TGs, RE corresponding to TG accepting EVEN-EVEN language,

Kleene's theorem part III (method 1:union of FAs), examples of FAs corresponding to simple REs, example of

Kleene's theorem part III (method 1) continued

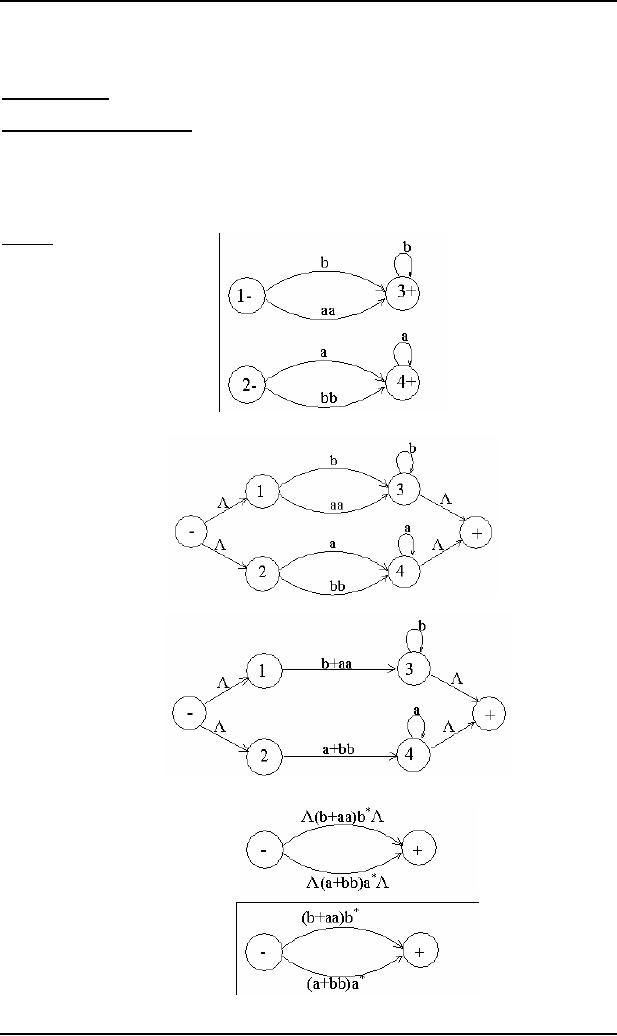
Example

Consider the following TG

To have single initial and single final state the above TG can be reduced to the following

To obtain single transition edge between 1 and 3; 2 and 4, the above can be reduced to the following

To eliminate states 1,2,3 and 4, the above TG can be reduced to the following TG

Theory of Automata

(CS402)

To connect the initial state with the final state by single transition edge, the above TG can be reduced to the

following

Hence the required RE is (b+aa)b*+(a+bb)a*

Example

Consider the following TG, accepting EVEN-EVEN language

1±

It is to be noted that since the initial state of this TG is final as well and there is no other final state, so to obtain

a TG with single initial and single final state, an additional initial and a final state are introduced as shown in the

following TG

To eliminate state 2, the above TG may be reduced to the following

To have single loop at state 1, the above TG may be reduced to the following

To eliminate state 1, the above TG may be reduced to the following

Hence the required RE is (aa+bb+(ab+ba)(aa+bb)*(ab+ba))*

Kleene's Theorem Part III

Statement:

If the language can be expressed by a RE then there exists an FA accepting the language.

Theory of Automata

(CS402)

As the regular expression is obtained applying addition, concatenation and closure on the letters of an alphabet

and the Null string, so while building the RE, sometimes, the corresponding FA may be built easily, as shown in

the following examples

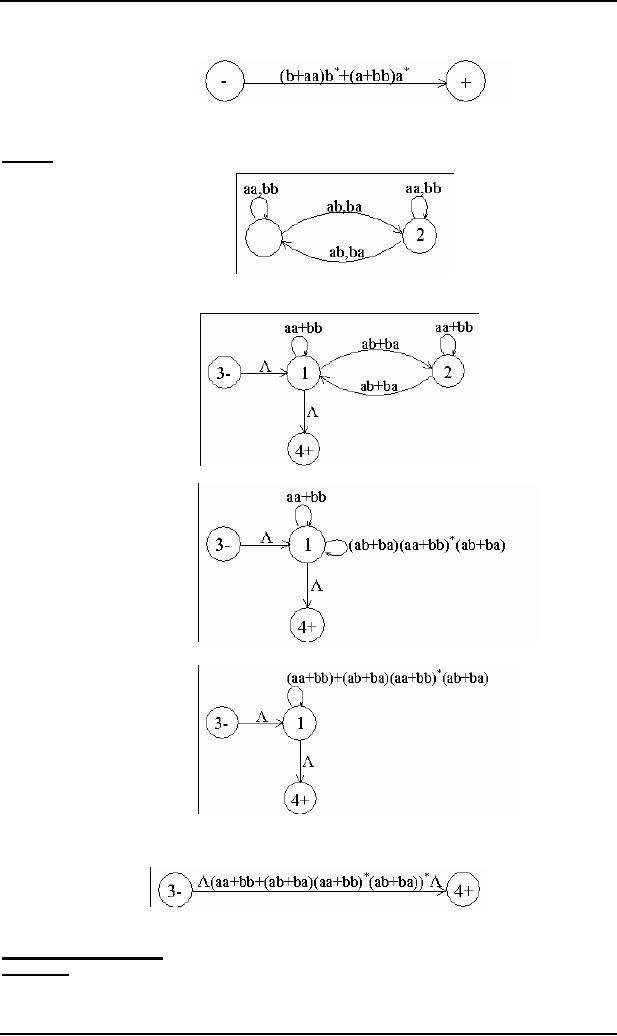
Example

Consider the language, defined over Σ = {a,b}, consisting of only b, then this language may be accepted by the

following FA

which shows that this FA helps in building an FA accepting only one letter

Example

Consider the language, defined over Σ = {a,b}, consisting of only Y, then this language may be accepted by the

following FA

As, if r1 and r2 are regular expressions then their sum, concatenation and closure are also regular expressions, so

an FA can be built for any regular expression if the methods can be developed for building the FAs

corresponding to the sum, concatenation and closure of the regular expressions along with their FAs. These

three methods are explained in the following discussion

Method1 (Union of two FAs): Using the FAs corresponding to r1 and r2 an FA can be built, corresponding to

r1+ r2. This method can be developed considering the following examples

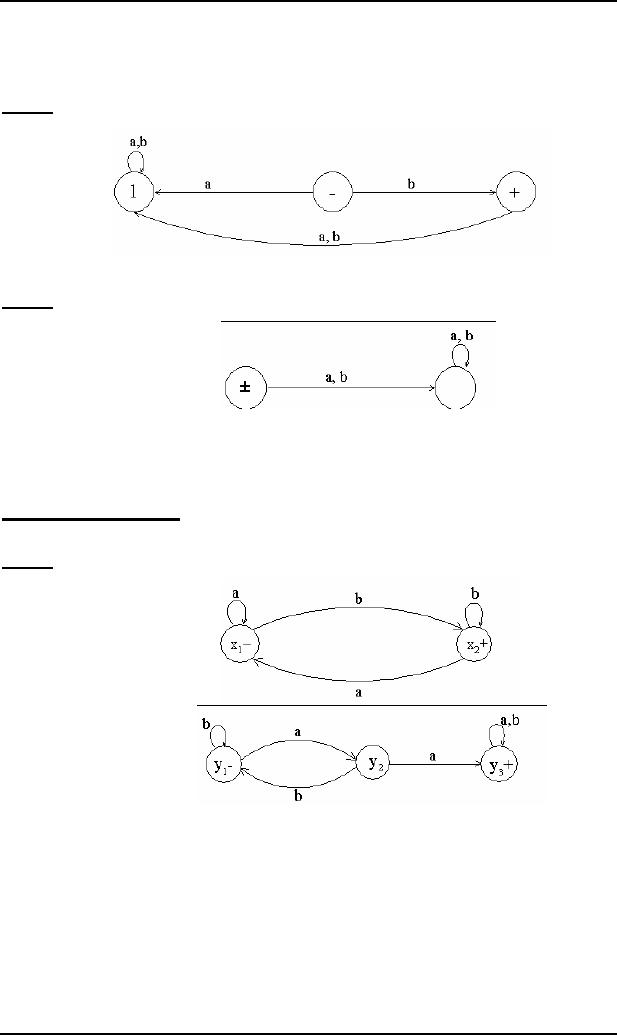
Example

Let r1 = (a+b)*b defines L1 and the FA1 be

and r2 = (a+b )*aa(a+b )* defines L2 and FA2 be

Let FA3 be an FA corresponding to r1+ r2, then the initial state of FA3 must correspond to the initial state of FA1

or the initial state of FA2.

Since the language corresponding to r1+ r2 is the union of corresponding languages L1 and L2, consists of the

strings belonging to L1or L2 or both, therefore a final state of FA3 must correspond to a final state of FA1 or FA2

or both.

Since, in general, FA3 will be different from both FA1 and FA2, so the labels of the states of FA3 may be

supposed to be z1,z2, z3, ..., where z1 is supposed to be the initial state. Since z1 corresponds to the states x1 or y1,

so there will be two transitions separately for each letter read at z1. It will give two possibilities of states either z1

or different from z1. This process may be expressed in the following transition table for all possible states of

FA3.

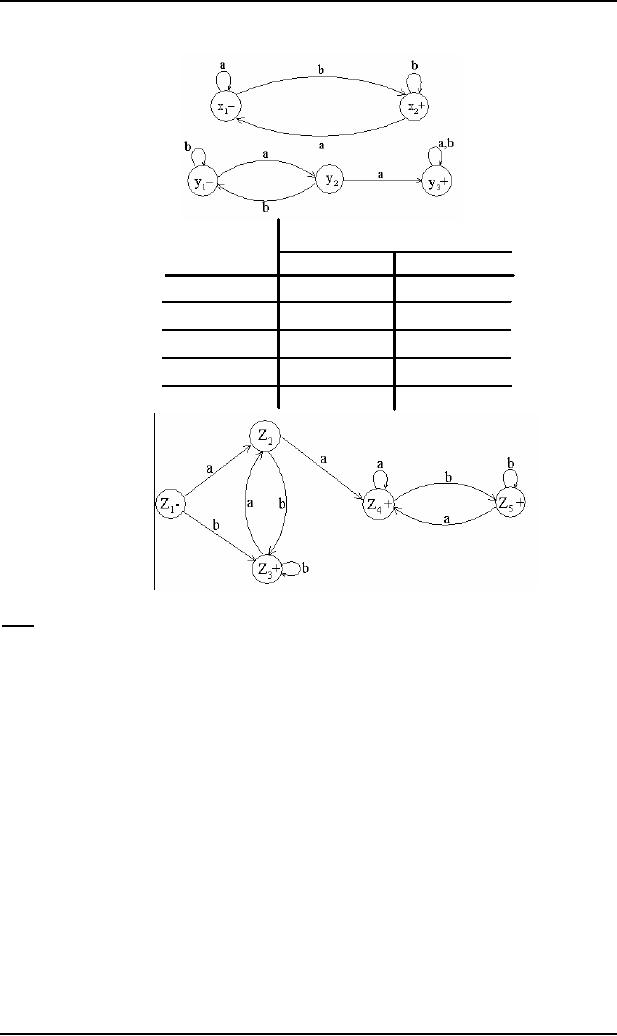
Theory of Automata

(CS402)

New States after reading

Old States

z1∫(x1,y1)

(x1,y2) ∫z2

(x2,y1) ∫ z3

z2 ∫(x1,y2)

(x1,y3) ∫z4

(x2,y1) ∫ z3

z3+ ∫(x2,y1)

(x1,y2) ∫ z2

(x2,y1) ∫ z3

z4+ ∫(x1,y3)

(x1,y3) ∫ z4

(x2,y3) ∫ z5

z5+ ∫(x2,y3)

(x1,y3) ∫ z4

(x2,y3) ∫ z5

RE corresponding to the above FA may be r1+r2 = (a+b)*b + (a+b )*aa(a+b )*.

Note: Further examples are discussed in the next lecture.

Table of Contents: