Proof(Kleene’s Theorem Part II)

<< Nondeterminism, Kleene’s Theorem

Kleene’s Theorem Part III >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 11

Reading Material

Chapter 7

Introduction to Computer Theory

Summary

proof of Kleene's theorem part II (method with different steps), particular examples of TGs to determine

corresponding REs.

Proof(Kleene's Theorem Part II)

To prove part II of the theorem, an algorithm consisting of different steps, is explained showing how a RE can

be obtained corresponding to the given TG. For this purpose the notion of TG is changed to that of GTG i.e. the

labels of transitions are corresponding REs.

Basically this algorithm converts the given TG to GTG with one initial state along with a single loop, or one

initial state connected with one final state by a single transition edge. The label of the loop or the transition edge

will be the required RE.

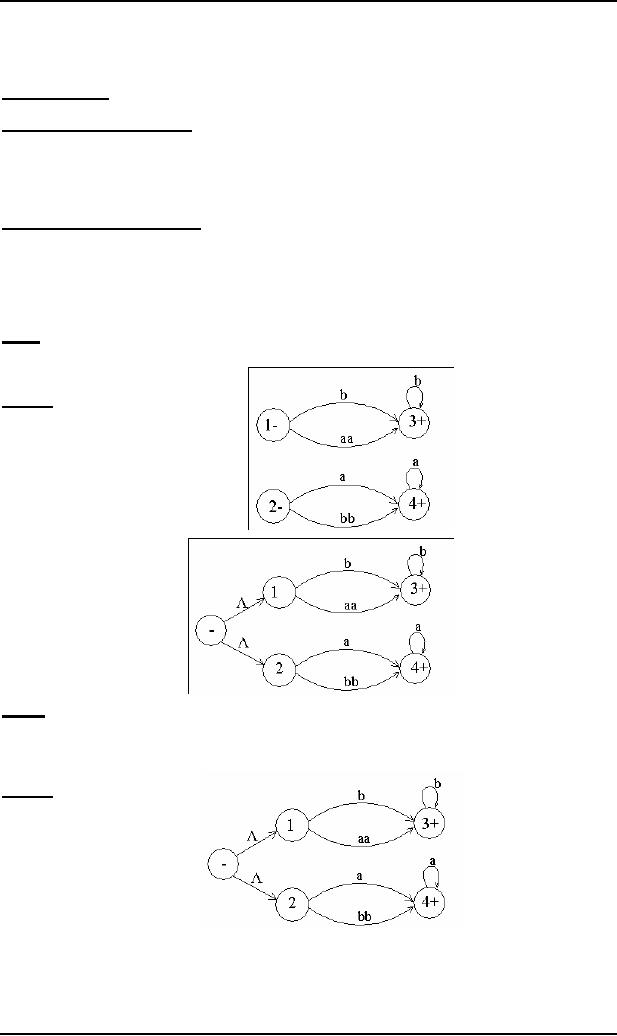
Step 1 If a TG has more than one start states, then introduce a new start state connecting the new state to the old

start states by the transitions labeled by Λ and make the old start states the non-start states. This step can be

shown by the following example

Example

The above TG can be converted to

Step 2:

If a TG has more than one final states, then introduce a new final state, connecting the old final states to the new

final state by the transitions labeled by Λ.

This step can be shown by the previous example of TG, where the step 1 has already been processed

Example

Theory of Automata

(CS402)

The above TG can be converted to

Step 3:

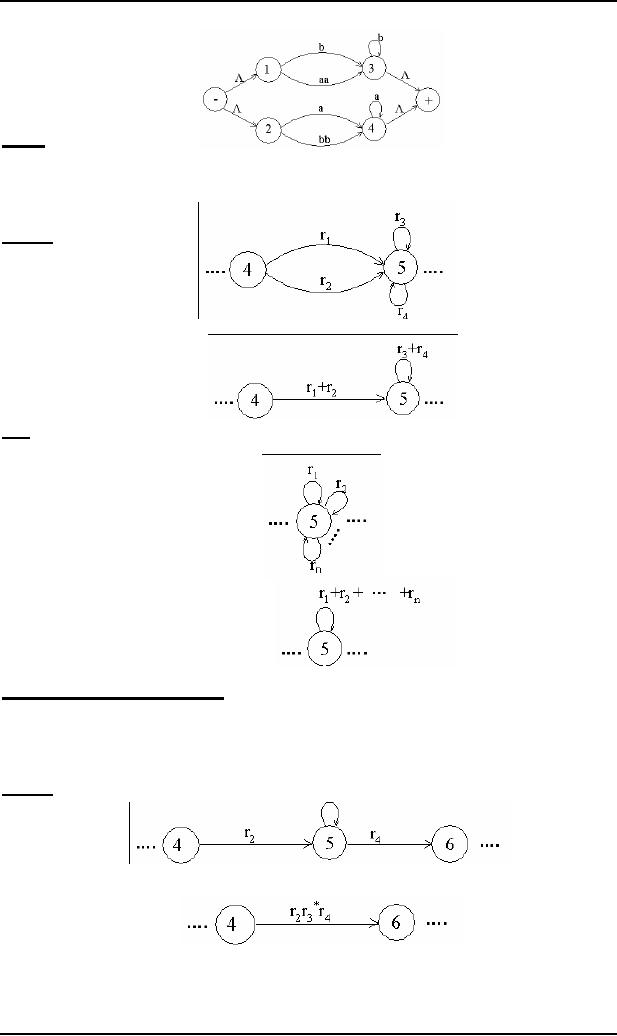
If a state has two (more than one) incoming transition edges labeled by the corresponding REs, from the same

state (including the possibility of loops at a state), then replace all these transition edges with a single transition

edge labeled by the sum of corresponding REs.

This step can be shown by a part of TG in the following example

Example

The above TG can be reduced to

Note

The step 3 can be generalized to any finite number of transitions as shown below

The above TG can be reduced to

Step 4 (bypass and state elimination)

If three states in a TG, are connected in sequence then eliminate the middle state and connect the first state with

the third by a single transition (include the possibility of circuit as well) labeled by the RE which is the

concatenation of corresponding two REs in the existing sequence. This step can be shown by a part of TG in the

following example

Example

To eliminate state 5 the above can be reduced to

Consider the following example containing a circuit

Theory of Automata

(CS402)

Example

Consider the part of a TG, containing a circuit at a state, as shown below

To eliminate state 3 the above TG can be reduced to

Example

Consider a part of the following TG

To eliminate state 3 the above TG can be reduced to

To eliminate state 4 the above TG can be reduced to

Note

It is to be noted that to determine the RE corresponding to a certain TG, four steps have been discussed. This

process can be explained by the following particular examples of TGs

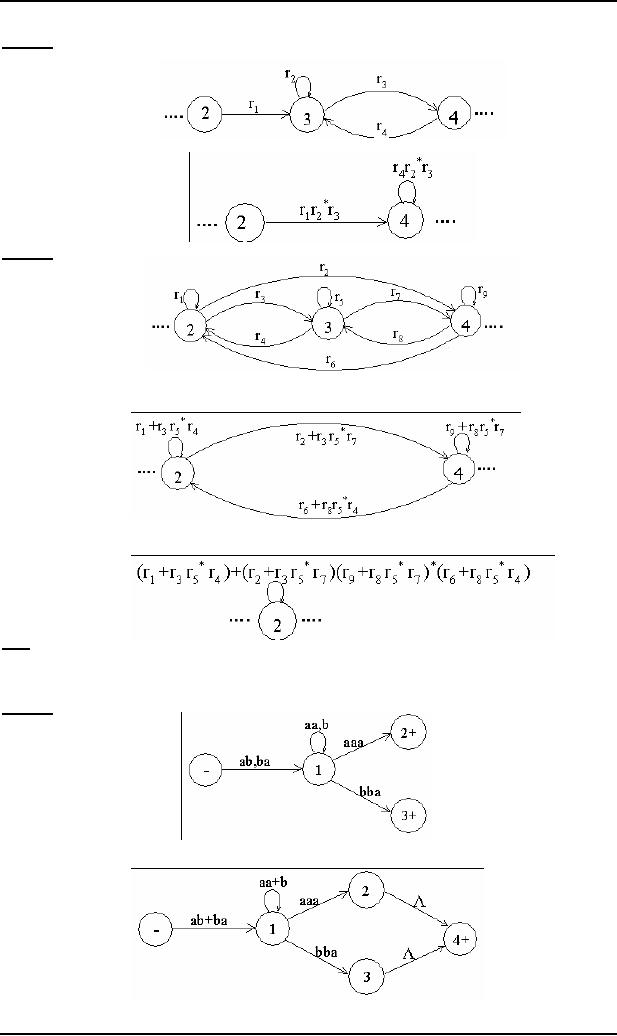
Example

Consider the following TG

To have single final state, the above TG can be reduced to the following

Theory of Automata

(CS402)

To eliminate states 2 and 3, the above TG can be reduced to the following

To eliminate state 1 the above TG can be reduced to the following

Hence the required RE is (ab+ba)(aa+b)*(aaa+bba)

Table of Contents: