What does automata mean, Introduction to languages

<< Table of Contents

Kleene Star Closure, Recursive definition of languages >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 1

Reading Material

Introduction to Computer Theory

Chapter 2

Summary

Introduction to the course title, Formal and In-formal languages, Alphabets, Strings, Null string, Words, Valid

and In-valid alphabets, length of a string, Reverse of a string, Defining languages, Descriptive definition of

languages, EQUAL, EVEN-EVEN, INTEGER, EVEN, { an bn}, { an bn an }, factorial, FACTORIAL,

DOUBLEFACTORIAL, SQUARE, DOUBLESQUARE, PRIME, PALINDROME.

What does automata mean?

It is the plural of automaton, and it means "something that works automatically"

Introduction to languages

There are two types of languages

Formal Languages (Syntactic languages)

Informal Languages (Semantic languages)

Alphabets

Definition

A finite non-empty set of symbols (called letters), is called an alphabet. It is denoted by Σ ( Greek letter sigma).

Example

Σ = {a,b}

Σ = {0,1} (important as this is the language which the computer understands.)

Σ = {i,j,k}

Note Certain version of language ALGOL has 113 letters.

Σ (alphabet) includes letters, digits and a variety of operators including sequential operators such as GOTO and

Strings

Definition

Concatenation of finite number of letters from the alphabet is called a string.

Example

If Σ = {a,b} then

a, abab, aaabb, ababababababababab

Note

Empty string or null string

Sometimes a string with no symbol at all is used, denoted by (Small Greek letter Lambda) λ or (Capital Greek

letter Lambda) Λ, is called an empty string or null string.

The capital lambda will mostly be used to denote the empty string, in further discussion.

Words

Definition

Words are strings belonging to some language.

Example

If Σ= {x} then a language L can be defined as

L={xn : n=1,2,3,.....} or L={x,xx,xxx,....}

Here x,xx,... are the words of L

Note

All words are strings, but not all strings are words.

Theory of Automata

(CS402)

Valid/In-valid alphabets

While defining an alphabet, an alphabet may contain letters consisting of group of symbols for example Σ1= {B,

aB, bab, d}.

Now consider an alphabet

Σ2= {B, Ba, bab, d} and a string BababB.

This string can be tokenized in two different ways

(Ba), (bab), (B)

(B), (abab), (B)

Which shows that the second group cannot be identified as a string, defined over

Σ = {a, b}.

As when this string is scanned by the compiler (Lexical Analyzer), first symbol B is identified as a letter

belonging to Σ, while for the second letter the lexical analyzer would not be able to identify, so while defining

an alphabet it should be kept in mind that ambiguity should not be created.

Remarks

While defining an alphabet of letters consisting of more than one symbols, no letter should be started with the

letter of the same alphabet i.e. one letter should not be the prefix of another. However, a letter may be ended in a

letter of same alphabet.

Conclusion

Σ1= {B, aB, bab, d}

Σ2= {B, Ba, bab, d}

Σ1 is a valid alphabet while Σ2 is an in-valid alphabet.

Length of Strings

Definition

The length of string s, denoted by |s|, is the number of letters in the string.

Example

Σ={a,b}

s=ababa

|s|=5

Example

Σ= {B, aB, bab, d}

s=BaBbabBd

Tokenizing=(B), (aB), (bab), (B), (d)

|s|=5

Reverse of a String

Definition

The reverse of a string s denoted by Rev(s) or sr, is obtained by writing the letters of s in reverse order.

Example

If s=abc is a string defined over Σ={a,b,c}

then Rev(s) or sr = cba

Example

Σ= {B, aB, bab, d}

s=BaBbabBd

Rev(s)=dBbabaBB

Defining Languages

The languages can be defined in different ways , such as Descriptive definition, Recursive definition, using

Regular Expressions(RE) and using Finite Automaton(FA) etc.

Descriptive definition of language

The language is defined, describing the conditions imposed on its words.

Theory of Automata

(CS402)

Example

The language L of strings of odd length, defined over Σ={a}, can be written as

L={a, aaa, aaaaa,.....}

Example

The language L of strings that does not start with a, defined over Σ ={a,b,c}, can be written as

L ={L, b, c, ba, bb, bc, ca, cb, cc, ...}

Example

The language L of strings of length 2, defined over Σ ={0,1,2}, can be written as

L={00, 01, 02,10, 11,12,20,21,22}

Example

The language L of strings ending in 0, defined over Σ ={0,1}, can be written as

L={0,00,10,000,010,100,110,...}

Example

The language EQUAL, of strings with number of a's equal to number of b's, defined over Σ={a,b}, can be

written as

{Λ ,ab,aabb,abab,baba,abba,...}

Example

The language EVEN-EVEN, of strings with even number of a's and even number of b's, defined over Σ={a,b},

can be written as

{Λ, aa, bb, aaaa,aabb,abab, abba, baab, baba, bbaa, bbbb,...}

Example

The language INTEGER, of strings defined over Σ={-,0,1,2,3,4,5,6,7,8,9}, can be written as

INTEGER = {...,-2,-1,0,1,2,...}

Example

The language EVEN, of stings defined over Σ={-,0,1,2,3,4,5,6,7,8,9}, can be written as

EVEN = { ...,-4,-2,0,2,4,...}

Example

The language {anbn }, of strings defined over Σ={a,b}, as

{an bn : n=1,2,3,...}, can be written as

{ab, aabb, aaabbb,aaaabbbb,...}

Example

The language {anbnan }, of strings defined over Σ={a,b}, as

{an bn an: n=1,2,3,...}, can be written as

{aba, aabbaa, aaabbbaaa,aaaabbbbaaaa,...}

Example

The language factorial, of strings defined over Σ={0,1,2,3,4,5,6,7,8,9} i.e.

{1,2,6,24,120,...}

Example

The language FACTORIAL, of strings defined over Σ={a}, as

{an! : n=1,2,3,...}, can be written as

{a,aa,aaaaaa,...}. It is to be noted that the language FACTORIAL can be defined over any single letter alphabet.

Example

The language DOUBLEFACTORIAL, of strings defined over Σ={a, b}, as

{an!bn! : n=1,2,3,...}, can be written as

{ab, aabb, aaaaaabbbbbb,...}

Example

The language SQUARE, of strings defined over Σ={a}, as

Theory of Automata

(CS402)

{an 2 : n=1,2,3,...}, can be written as

{a, aaaa, aaaaaaaaa,...}

Example

The language DOUBLESQUARE, of strings defined over Σ={a,b}, as

{an 2 bn 2 : n=1,2,3,...}, can be written as

{ab, aaaabbbb, aaaaaaaaabbbbbbbbb,...}

Example

The language PRIME, of strings defined over Σ={a}, as

{ap : p is prime}, can be written as

{aa,aaa,aaaaa,aaaaaaa,aaaaaaaaaaa...}

An Important language

PALINDROME

The language consisting of Λ and the strings s defined over Σ such that Rev(s)=s.

It is to be denoted that the words of PALINDROME are called palindromes.

Example

For Σ={a,b},

PALINDROME={Λ , a, b, aa, bb, aaa, aba, bab, bbb, ...}

Remark

There are as many palindromes of length 2n as there are of length 2n-1.

To prove the above remark, the following is to be noted:

Note

Number of strings of length `m' defined over alphabet of `n' letters is nm.

Examples

The language of strings of length 2, defined over Σ={a,b} is L={aa, ab, ba, bb} i.e. number of strings = 22

The language of strings of length 3, defined over Σ={a,b} is L={aaa, aab, aba, baa, abb, bab, bba, bbb} i.e.

number of strings = 23

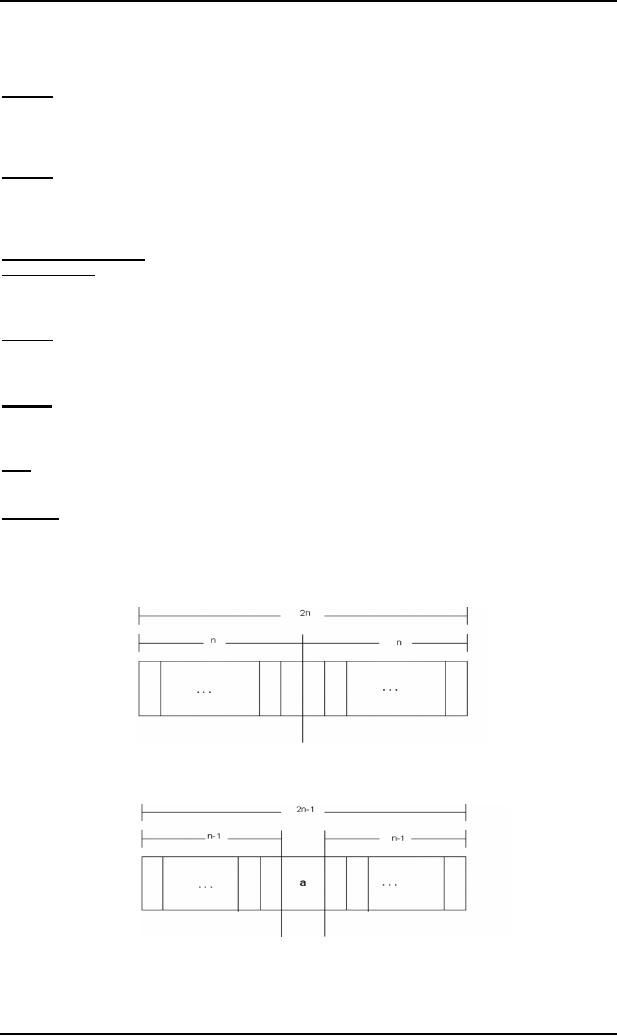
To calculate the number of palindromes of length(2n), consider the following diagram,

which shows that there are as many palindromes of length 2n as there are the strings of length n i.e. the required

number of palindromes are 2n.

To calculate the number of palindromes of length (2n-1) with `a' as the middle letter, consider the following

diagram,

which shows that there are as many palindromes of length 2n-1 as there are the strings of length n-1 i.e. the

required number of palindromes are 2n-1.

Theory of Automata

(CS402)

Similarly the number of palindromes of length 2n-1, with ` b ' as middle letter, will be 2n-1 as well. Hence the

total number of palindromes of length 2n-1 will be 2n-1 + 2n-1 = 2 (2n-1)= 2n .

Table of Contents: