Stream Manipulations, Manipulators, Non Parameterized Manipulators, Formatting Manipulation

<< Source and Destination of streams, Formatted Input and Output, Buffered Input/Output

Overloading Insertion and Extraction Operators >>

CS201 Introduction to Programming

Lecture Handout

Introduction to Programming

Lecture No. 36

Reading Material

Deitel & Deitel - C++ How to Program

Chapter. 11

11.6, 11.7

Summary

37)

Stream Manipulations

38)

Manipulators

39)

Non Parameterized Manipulators

40)

Parameterized Manipulators

41)

Format State Slags

42)

Formatting Manipulation

43)

Showing the Base

44)

Scientific representation

45)

Exercise

Stream Manipulations

After having a thorough look into the properties and object definition of I/O streams, we

will discuss their manipulations. Here, there is need of some header files to include in our

program the way, cin and cout are used. We include iostream.h and fstream.h while using

file manipulations. In case of manipulation of the I/O streams, the header file with the

name of iomanip.h is included. It is required to be included whenever there is need of

employing manipulators.

As discussed earlier, we can determine the state of a stream. The states of the stream can

be determined. For example, in case of cin, we can check where the end of file comes.

For state- checking, these stream objects have set of flags inside them. These flags can be

considered as an integer or long integer. The bit position of these integers specifies some

specific state. There is a bit for the end of file to test. It can be written as under:

cin.eof() ;

Page 458

CS201 Introduction to Programming

It will return the state of end of file. The bit will be set if the file comes to an end.

Similarly, there is a fail bit. This bit determines whether an operation has failed or not.

For example, an operation could be failed due to a formatting error. The statement

cin.fail; will return the value of the fail bit. As this statement returns a value, we can use

it in an `if statement' and can recover the error. Then there is a bad bit. This bit states that

data has lost. The presence of this bit means that some data has lost during I/O operation.

So we can check it in the following manner.

cin.bad();

It can be used in parentheses as a function call that will allow us to check whether the

operation failed or successful. Similarly we can also check for' good', that is a bit

showing that everything is good. This bit will be set if fail and bad bits are not set. We

can check this bit as cin.good ; and can find out whether the input operation was

successful. If some bit like bad has been set, there should also be a mechanism to clear it.

For this, we have

cin.clear() ;

as a member function for these objects. This will reset the bits to their normal good state.

This is a part of checking input stream.

Manipulators

Whenever carrying out some formatting, we will want that the streams can manipulate

and a number should be displayed in a particular format. We have stream manipulators

for doing this. The manipulators are like something that can be inserted into stream,

effecting a change in the behavior. For example, if we have a floating point number, say

pi (л), and have written it as float pi = 3.1415926 ; Mow there is need of printing the

value of pi up to two decimal places i.e. 3.14 . This is a formatting functionality. For this,

we have a manipulator that tells about width and number of decimal points of a number

being printed. Some manipulators are parameter less. We simply use the name of the

manipulator that works. For example, we have been using endl, which is actually a

manipulator, not data. When we write cout << endl ; a new line is output besides

flushing the buffer. Actually, it manipulates the output stream. Similarly flush was a

manipulator for which we could write cout << flush that means flushing the output

buffer. So it manipulates the output.

A second type of manipulators takes some argument. It can be described with the help of

an example. Suppose we want to print the value of pi up to two decimal places. For this

purpose, there should be some method so that we can provide the number i.e. two (2) up

to which we want the decimal places. This is sent as a parameter in the manipulators.

Thus we have the parameterized manipulators.

Let's have a look on what streams do for us. We know that streams are like ordered

sequence of bytes and connect two things i.e., a source and a destination. In the middle,

the stream does some conversion. So it may take some binary representation of some

information and convert it into human readable characters. It may also take characters

Page 459

CS201 Introduction to Programming

and convert them into an internal representation of data. With in the conversion of data,

we can do some other things. For example, you might have seen that if a system prints

computerized cheques, it puts some special characters with the numbers. If there is a

cheque for four thousand rupees, this amount would be written on it as ****4000.00. The

idea of printing * before the amount is that no body could insert some number before the

actual amount to change it. As we don't want that somebody has increased the amount on

the cheque from Rs 4000 to Rs 14000.The printing of * before the amount is a

manipulation that we can do with input or output objects. We can also tell the width for a

number to be printed. So there are many conversions that we can do. We can use fill

characters like * as mentioned in the example of cheque printing. To accomplish all these

tasks, there are different methods. So it becomes a little confusing that the same work is

being done through 2-3 different methods. Some are inline manipulators like endl. We

can use it with << and write inline as cout << endl ; The same work could be done with

the flush method. We could also write cout.flush ; Thus it is confusing that there is an

inline manipulator and a function for the same work.

Non-Parameterized Manipulators

Let's start with simple manipulators. We have been dealing with numbers like integers,

floats etc for input and out put. We know that our number representations are associated

with some base. In daily life, the numbers of base 10 are used in arithmetic. When we see

4000 written on a cheque, we understand that it is four thousands written in the decimal

number system (base 10). But in the computer world, many systems are used for number

representation that includes binary (base 2), octal (base 8), decimal (base 10) and

hexadecimal (base 16) systems. A simple justification for the use of these different

systems is that computers internally run on bits and bytes. A byte consists of eight bits.

Now if we look at the values that can be in eight bits. 256 values (from 0 to 255 ) can be

stored in eight bits. Now consider four bits and think what is the highest number that we

can store in four bits. We know that the highest value in a particular number of bits can

be determined by the formula 2n - 1 (where n is the number of bits). So the highest value

that can be stored in four bits will be 24 - 1 i.e. 15. Thus the highest value, we can store in

four bits is 15 but the number of different values that can be stored will be 2n i.e. 16

including zero. Thus we see that while taking half of a byte i.e. four bits, 16 (which is the

base of hexadecimal system) different numbers can be stored in these four bits. It means

that there is some relationship between the numbers that have a base of some power of

two. So they can easily be manipulated as bit format. Thus four bits are hex. What about

eight (octal)? If we have three bits, then it is 23 = 8, which is the base of octal system.

Thus, we can use three bits for octal arithmetic.

We can use manipulators to convert these numbers from one base to the other. The

manipulators used for this purpose, can be used with cin and cout. These are non-

parameterized manipulators. So if we say the things like int i = 10 ; Here i has the

decimal value 10. We write cout << i ; and 10 is being displayed on the screen. If we

want to display it in octal form, we can use a manipulator here. If we write

cout << oct << i ;

Page 460

CS201 Introduction to Programming

it will display the octal value of i (10) which is 12. This manipulator converts the

decimal number into an octal number before displaying it. So the octal representation of

10 which is 12, will be displayed on the screen. Similarly if we write

cout << hex << i ;

Here hex stands for the hexadecimal. hex is the manipulator that goes into the out put

stream before i and manipulates the stream by converting the decimal number into a

hexadecimal number. As a result, the hexadecimal value of 10 is displayed on the screen.

If we have a number in octal or hexadecimal system , it can be converted into a decimal

number by putting the dec manipulator in the stream like

cout << dec << i ;

These (oct, hex and dec) are very simple inline manipulators without any argument.

There is also a manipulator for white space. The white space has a special meaning. It is a

delimiter that separates two numbers (or words). In cin and cout, the white space acts as a

delimiter. If we want that it should not act as a delimiter, it can used as a ws manipulator.

This manipulators skips white space. This manipulator takes no argument. This ws

manipulator is sometime useful but not all the times. The following table shows the non-

parameterized manipulators and their description.

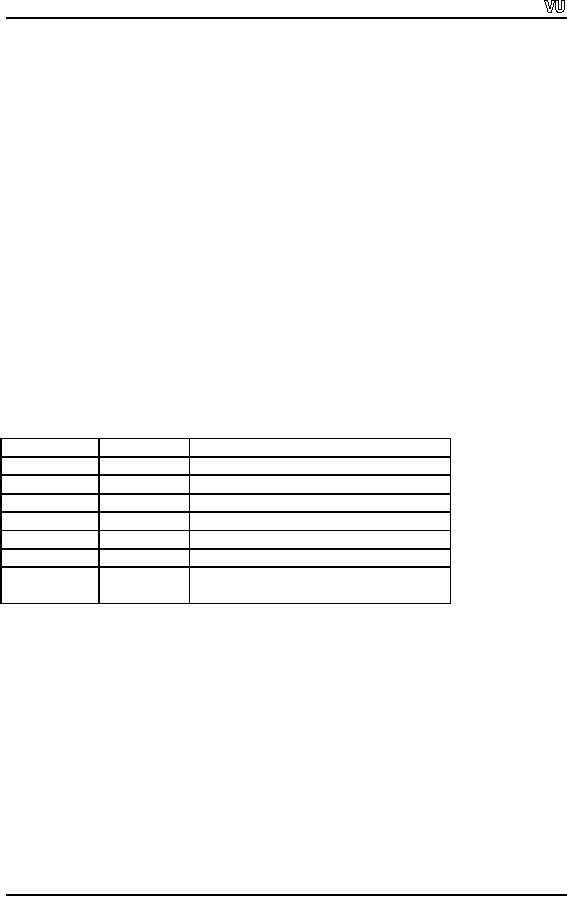
Manipulator

Domain

Effect

dec

In / Out

Use decimal conversion base

hex

In / Out

Use hexadecimal conversion base

oct

In / Out

Use octal conversion base

endl

Output

Inserts a new line and flush the stream

ends

Output

Terminate a string with NULL

flush

Output

Flush the stream

Input

Skip leading whitespace for the next

string extraction only

The base becomes important while doing programming of scientific programs. We may

want that there is the hexadecimal presentation of a number. We have discussed the

justification of using hexadecimal or octal numbers, which is that they match with bits.

Here is another justification for it. Nowadays, computers are just like a box with a button

in front of them. A reset button is also included with the main power button. While seeing

the pictures or in actual Miniframe and mainframe computers, you will notice that there

is a row of switches in front of them. So there are many switches in front of these

computers that we manipulate. These switches are normally setting directly the values of

registers inside the computer. So you can set the value of register as 101011 etc by

switching on and off the switches. We can do that to start a computer or signaling

something to computer and so on. There are a lot of switches in front of those computers

ranging between 8 to 16. You have to simply remember what is the value to start the

computer. Similarly, it will require the reading the combinations of switches from the

paper to turn on the computer. This combination tells you which switch should be on and

Page 461

CS201 Introduction to Programming

which should be off. As a human being instead of remembering the whole pattern like

10110000111 etc, it could be easy to remember it as 7FF. Here we are dealing with HEX

numbers. For the digit 7, we need four bits. In other words, there is need to set four

switches. The pattern of 7 is 0111. So we set 7 with this combination. For F, all the four

bits should be on as 1111 and so on. Thinking octal and hexadecimals straight away maps

to the bits. It takes a little bit of practice to effectively map on the switches. On the other

hand, decimal does not map to those bits. What will be its octal number in case of

decimal number 52.? You have to calculate this. What is the binary representation of 52?

Again you have to calculate. There are a lot of things which you have to calculate. On the

hand, if we say 7ABC in case of HEX, we are mapping the number straight away on four

bits. In octal system, we map the number on three bits. A is ten so it will be 1010 so you

can quickly set the switches. It may not be relevant today. But when you are working

with big computers, it will become quite relevant. There are many times when we have to

manipulate binary data using mechanical device while thinking in hexadecimal and octal

terms. In the language, you have the facility to set the base. You can use setbase(), hex,

oct, dec and setf. There are many ways of doing the same thing. Programmers write these

languages. Therefore they make this facility available in the language as built in.

Parameterized Manipulators

Suppose we want to print the number 10 within a particular width. Normally the numbers

are written right justified. In case of no action on our part, cout displays a number left

justified and in the space required by the number. If we want that all numbers should be

displayed within the same particular width, then the space for the larger number has to be

used. Let's say this number is of four digits. Now we want that there should be such a

manipulator in the output that prints every number in a space of four digits. We have a

manipulator setw (a short for set width), it takes as an argument the width in number of

spaces. So to print our numbers in four spaces we write

cout << setw(4) << number ;

When printed, this number gets a space of four digits. And this will be printed in that

space with right justification. By employing this mechanism, we can print values in a

column (one value below the other) very neat and clean.

Now in the example of printing a cheque, we want that the empty space should be filled

with some character. This is required to stop somebody to manipulate the printed figure.

To fill the empty space, there is need of manipulator setfill. We can write this

manipulator with cout as the following

cout << setfill (character) ;

where the character is a single character written in single quotes. Usually, in cheque

printing, the character * is used to fill the empty spaces. We can use any character for

example, 0 or x. The filling character has significance only if we have used setw

manipulator. Suppose, we are going to print a cheque with amount in 10 spaces. If the

amount is not of 10 digits, the empty space will be filled with *. Thus the usage of setfill

Page 462

CS201 Introduction to Programming

is there where we use setw for printing a number in a specific width. So if we want to

print an amount in 10 spaces and want to fill the empty spaces with *, it can be written as

under.

cout << setfill(*) << setw(10) << amount ;

Thus the manipulators can also be of cascading nature. The stream insertion operator

(<<) is overloaded and every overload of it returns a reference to the cout object itself.

This means that while working from left to right, first the fill character will be set

returning a reference to cout . Later, its width will be set to 10 character and return a

reference to cout again. Finally, the amount will be displayed in the required format.

Thus, we have manipulated the stream in two ways. Example of a pipe with two bends

can help it understand further. Now whatever figure goes into it, its width and the fill

character is set and things are displayed in the space of 10 characters. If we want to print

an amount of Rs 4000 on the cheque, it will be printed on the cheque as ******4000.

Thus, we have two manipulators, setw and setfill which are used with cout.

Let's further discuss the same example of cheque. In real world, if we look at a computer

printed cheque , the amount is printed with a decimal point like 4000.00 even if there is

no digit after decimal point. We never see any amount like 4000.123, as all the currencies

have two- digit fractional part. Thus, we examine that the fractional part has been

restricted to two decimal places. The decimal digits can be restricted to any number. We

have a manipulator for this purpose. The manipulator used for this purpose is

setprecision. This is a parameterized manipulator. It takes an integer number as an

argument and restrict the precision to that number. If we write

cout << setprecision (2) << float number ;

The above statement will display the given float number with two decimal places. If we

have the value of pi stored in a variable, say pi, of type float with a value of 3.1415926

and want to print this value with two decimal places. Here, manipulator setprecision can

be used. It can be written as under.

cout << setprecision (2) << pi ;

This will print the value of pi with two decimal places.

Now think about it and write on the discussion board that whether the value of pi is

rounded or truncated when we print it with setprecision manipulator. What will be the

value of pi with five decimal places and with four decimal places? Will the last digit be

rounded or the remaining numbers will be truncated?

At this point, we may come across some confusion. We have learned the inline

manipulators that are parameter less. For these, we simply write cout << hex <<

number; which displays the number in hexadecimal form. There is also a parameterized

manipulator that performs the same task. This manipulator is setbase. It takes the base of

the system (base, to which we want to format the number) as an argument. Instead of

Page 463

CS201 Introduction to Programming

using oct, dec and hex manipulators, we can use the setbase manipulator with the

respective base as an argument. So instead of writing

cout << oct << number ;

we can write

cout << setbase (8) << number ;

The above two statements are equivalent in the way for having the same results. It is a

matter of style used by one of these manipulators. We can use either one of these,

producing a similar effect. The cout << setbase(8) means the next number will be printed

in the base 8. Similarly cout << setbase(16) means the next number will be printed in

hexadecimal (base 16) form. Here a point to note is that setbase (0) is the same as

setbase(10).

Following is the table, in which the parameterized manipulators with their effect are

listed.

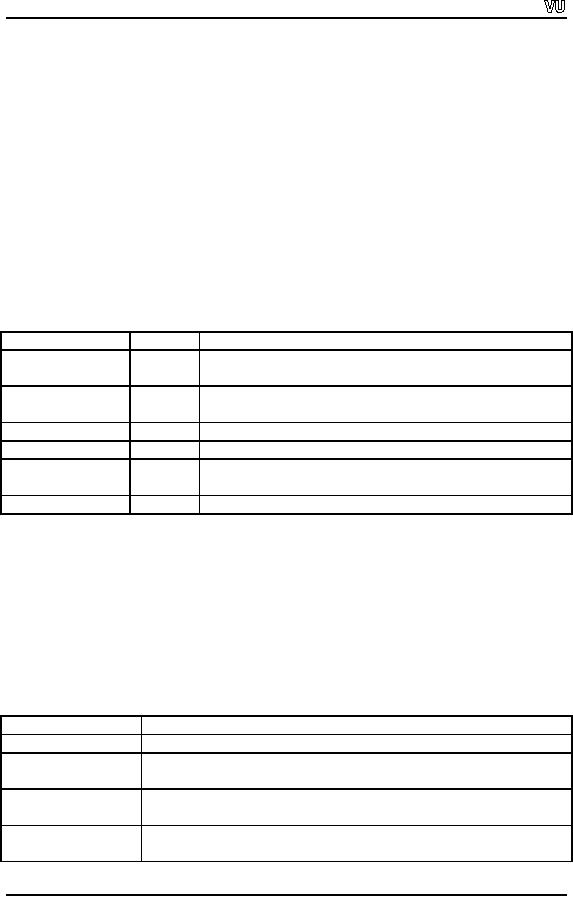
Manipulator

Domain

Effect

resetioflags(long

In / Out

Clear flags specified in f

setbase (int b)

In / Out

Set numeric conversion base to b (b may be 0, 8, 10 or

16)

setfill (int c)

Output

Set fill character to c

setiosflags(long f)

In / Out

St flags specified in f

setprecision (int

Output

Set floating point precision to p

setw (int w)

Output

Set field width to w

Format State Flags

We have discussed that there are flags with the stream objects. This set of flags is used to

determine the state of the stream. The set includes good, fail, eof etc that tells the state of

the stream. There is also another set of flags comprising the ones for input/output system

(ios). We can use setioflag, and give it as an argument a long number. Different bit values

are set in this number and the flags are set according to this. These flags are known as

format state flags and are shown in the following table. These flags can be controlled by

the flags, setf and unsetf member functions.

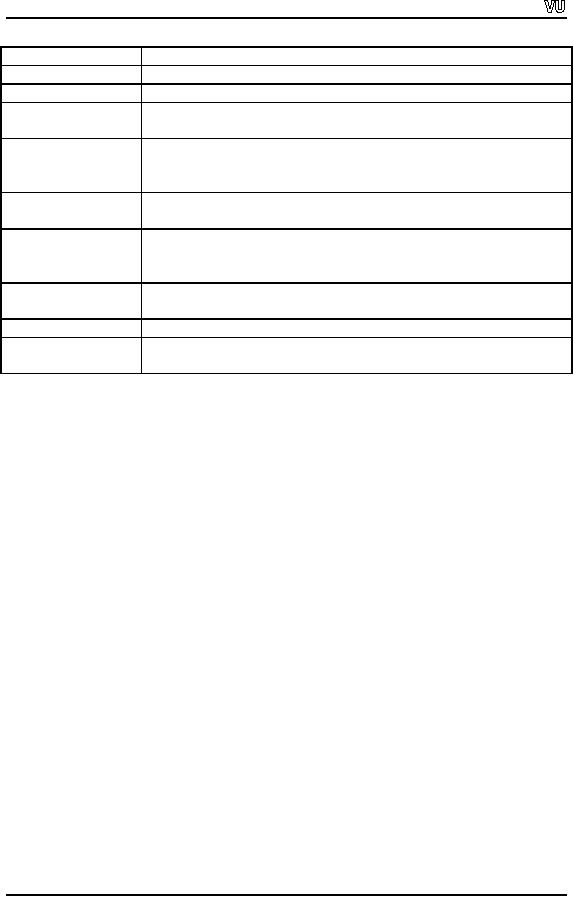
Format state flag

Description

ios::skipws

Skip whitespace character on an input stream.

ios::left

Left justify output in a field, padding characters appear to the right

if necessary.

ios::right

Right justify output in a field, padding characters appear to the left

if necessary.

ios::internal

Indicate that a number's sign should be left justified in a field and

a number's magnitude should be right justified in that same field

Page 464

CS201 Introduction to Programming

(i.e. padding characters appear between the sign and the number).

ios::dec

Specify that integers should be treated as decimal (base 10) values.

ios::oct

Specify that integers should be treated as octal (base 8) values.

ios::hex

Specify that integers should be treated as hexadecimal (base 16)

values.

ios::showbase

Specify that the base of a number is to be output ahead of the

number(a leading 0 for octals, a leading 0x or 0X for

hexadecimals).

ios::showpoint

Specify that floating-point numbers should be output with a

decimal point. This is normally used with ios::fixed.

ios::uppercase

Specify that uppercase letters (i.e X and A through F) should be

used in the hexadecimal integers and the uppercase E in scientific

notation.

ios::showpos

Specify that positive and negative numbers should be preceded by

a + or - sign, respectively.

ios::scientific

Specify output of a floating-point value in scientific notation.

ios::fixed

Specify output of a floating-point value in fixed point notation

with a specific number of digits to the right of the decimal point.

Let's talk about more complicated things. We discussed a parameterized manipulator

setw that sets the width to print in the output. There is an alternative for it i.e. the member

function, called `width()'. This function also takes the same parameter and an integer, in

which width the things are to display or read. This function applies to both input and

output stream. For this, we write cin.width (7). This will create a format field of the width

of 7 characters for an input. Now we write cout.width (10) ; this will set the width of

output field to 10. With it, the next number to be printed will be printed in 10 spaces.

Thus setw, inline manipulator has the alternative function cin.width and cout.width with

single argument.

It equally applies to the setprecision. This is the parameterized, inline- manipulator that

sets the places after the decimal point. There is a member function as well in these

objects that is precision. The setprecision is an inline manipulator, used along with

stream insertion (<<). If we want to do the same thing with a function call,

cout.precision(2) is written. It has the same effect as that of cout << setprecision (2).

Thus we have different ways of doing things.

We have used setfill manipulator. Here is another member- function i.e. cout.fill. The

behavior of this function is exactly the same. We simply write cout.fill(`*') ; identical to

cout << setfill(`*'). The filling character is mostly used whenever we use financial

transactions but not necessarily. We can also use zero to fill the space.

So fill and setfill, width and setw, precision and setprecision and almost for every inline

manipulator, there are member functions that can be called with these streams.

The member functions are defined in iostream.h. However, the manipulators are defined

in iomanip.h. Normally we have been including iostream.h in our programs to utilize the

member functions easily. But inclusion of a header file `iomanip.h file is must for the use

of manipulators.

Page 465

CS201 Introduction to Programming

We should keep in mind that when we can write inline manipulators in the following

fashion.

cout << setw (7) << i ;

And in the next line we write

cout << j ;

Here the setw manipulator will apply to i only and not after that to j. This means that

inline manipulators apply only to the very next piece of data i.e. output. It does not apply

to subsequent output operations.

Formatting Manipulation

We can adjust the output to left side, right side or in the center. For this purpose, we have

a member function of the object whose syntax is as under:

cout.setf(ios:: flag, ios:: adjust field)

The setf is a short for set flag. The flags are long integers, also the part of the objects.

They are the bit positions, representing something. Here we can set these flags. The flags

of adjustfield are set with values i.e. left, right, left | right and internal. The description of

these is as follows.

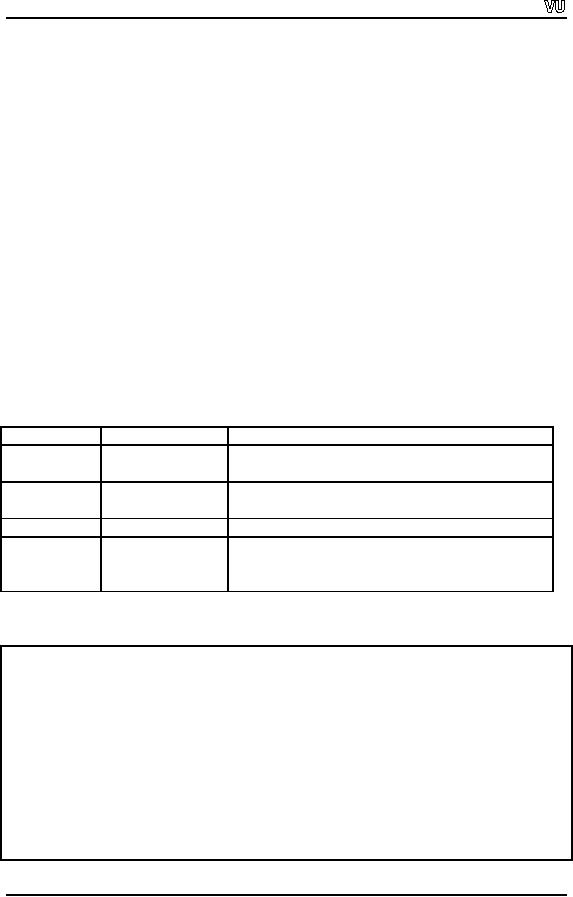
Value of flag

Meaning

Description

left

Left-justify

Justifies the output to left side

output

right

Right-justify

Justifies the output to right side

output

left | right

Center output

Centralized the output

internal

Insert padding

Places padding between signs or base indicator

and the first digit of a number. This applies only

to number values and not to character array.

Following is the code of a program that shows the effects of these manipulators.

//This program demonstrate the justified output

#include <iomanip.h>

#include <iostream.h>

void main()

{

int i = -1234;

cout.setf(ios::left, ios::adjustfield);

cout << "|" << setw(12) << i << "|" << endl;

cout.setf(ios::right, ios::adjustfield);

cout << "|" << setw(12) << i << "|" << endl;

Page 466

CS201 Introduction to Programming

cout.setf(ios::internal, ios::adjustfield);

cout << "|" << setw(12) << i << "|" << endl;

cout.setf(ios::left | ios::right,

ios::adjustfield);

cout << "|" << setw(12) << i << "|" << endl;

cin >> i ;

}

Following is the output of the above program.

|-1234

-1234|

1234|

-1234|

We have discussed two types of manipulators for base, the parameter less manipulator in

which we look for oct, dec and hex. On the other hand, there is a parameterized

manipulator setbase which takes an integer to set the base. It uses 0 or 10 for decimal, 8

for octal and 16 for hexadecimal notations.

Now we have a generic function setf that sets the flags. We can write something like

cout.setf(ios::hex)

The hex is defined in ios. It has the same effect. It sets the output stream, in this case

cout, to use hexadecimal display for integers. So it is the third way to accomplish the

same task. The use of these ways is a matter of programming style.

Showing the base

Now there should be someway to know which base has the number output by the

programmer. Suppose we have a number 7ABC, then it be nothing but hexadecimal.

What will be the nature of 7FF. It is hexadecimal. However, the number 77 (seven seven)

is a valid number in all of different basis. We have a built-in facility showbase. It is a

flag. We can set the showbase for output stream that will manipulate the number before

displaying it. If you have the showbase falg on (by default it is off), a number will be

displayed with special notations. The setf function is used to set the flag for the base field.

Its syntax is as under:

cout.setf(ios::base, ios::basefield);

Here base has three values i.e. oct, dec and hex for octal, decimal and hexadecimal

systems respectively. If the basefield is set to oct (octal), it will display the number with a

preceding zero. It shows that the number is in octal base. If the basefield is set to hex

(hexadecimal), the number will be displayed with a preceding notation 0x. The number

will be displayed as such if the basefield is set to dec (decimal). If there is a number, say

77, it will be difficult to say that it is in octal, decimal or hexadecimal base, a valid

number for all the three systems. However, if we output it with the use of showbase, it

will be easy to understand in which base the output number is being represented. The

Page 467

CS201 Introduction to Programming

following example, demonstrates this by showing the number (77) along with the base

notation.

/* This program demonstrate the use of show base.

It displays a number in hex, oct and decimal form.

#include <iostream.h>

void main()

{

int x = 77;

cout.setf(ios::showbase);

cout.setf(ios::oct,ios::basefield); //base is 8

cout << x << '\n';

//displays number with octal notation

cout.setf(ios::hex,ios::basefield); //base is 16

cout << x << '\n';

//displays number with hexadecimal notation

cout.setf(ios::dec,ios::basefield);

cout << x << '\n';

}

Following is the output of the program.

0115

0x4d

Scientific Representation

When the numbers get bigger, it becomes difficult to write and read in digits format. For

example, one million will be written as 1000000. Similarly hundred million will be

100000000 (one with eight zeros). How will we display the number which is of 20-digit

long? For this, we use scientific notation. To do it, a manipulator ios:: scientific can be

used. If the flag in setf to the scientific is set, it can be written as

cout.setf(ios::scientific, ios::floatfield) ;

Then the floating point numbers will be displayed in scientific notation. A number in

scientific is like 1.946000e+009. So we can set the state of output stream to use scientific

notation for outputting a number.

To do the scientific notation off and restore the default notation, we set the flag in setf

function to fixed (which is a short for fixed point notation). This can be written as

cout.setf(ios::fixed, ios::floatfield) ;

Page 468

CS201 Introduction to Programming

Uppercase/Lowercase Control

Similarly, we have a manipulator ios::uppercase. While using this manipulator, the e in

scientific notation is written in uppercase i.e. E. If we are using hexadecimal numbers,

then the characters of it will be displayed in uppercase letters as A, B, C, D, E and F.

Exercise

We have been using matrices i.e. a two dimensional array. As an exercise, try to

print out a matrix of three rows and three columns, in such a way that it should be

nicely formatted. The numbers should be aligned as we write it in a neat and clean

way on the paper. You can use the symbol | at the start and end of each row as we

don't have a so big square bracket to put around three rows. To be more elegant to

print a matrix, we can use a proper graphic symbol to put square brackets around

the matrix instead of using | symbol. In the ASCII table, there are many symbols

that we can use to print in our programs. We have the integer values of these

symbols in the table. Suppose you have a value 135 of a symbol. Now to print this

symbol, press the `alt' key and keeping the key pressed enter the integer value i.e.

135 from the num pad of the key board, release the `alt' key. Now you will see

that symbol on the screen. For the value 135, the symbol is ç. In programming, we

can provide this symbol to be printed as a single character in single quotes. For

this, put a single quote and then enter the symbol in the way stated above and then

put the single quote. It will be written as `ç'. Find out proper symbols from the

ASCII table that can comprise to put a square bracket around the matrix.

Write simple programs to demonstrate the use of different manipulators and

examine their effects.

Page 469

Table of Contents: