 |

CS201
Introduction to Programming
Lecture
Handout
Introduction
to Programming
Lecture
No. 21
Reading
Material
Deitel
& Deitel - C++ How to
Program
Chapter.
16
16.7
Summary
·
Bit
Manipulation
·
Bit
Manipulation Operators
·
AND
Operator
·
OR
Operator
·
Exclusive
OR Operator
·
NOT
Operator
Bit
Flags
Masking
Unsigned
Integers
·
Sample
Program
·
Shift
Operators
Bit
Manipulation
We have
so far been dealing with bytes
using different data types.
In this lecture, we
will
see
what a bit is? Bit is
the basic unit of memory.
Eight bits form a byte. As you
know
that
data is stored in computers in
0's and 1's form. An
integer uses four bytes
and the
integer
calculations occur in four bytes.
Thus, we are manipulating
bytes while using
different
data types. Now we will
try to understand the
process of `bit
manipulation'.
Now we
will deal with each
bit in a byte and explore how to do on or
off each bit. A
bit,
having 1 is
said on while the one
with 0 is called off. Here we will
discuss different
operators
to manipulate bits.
The
concept of bit manipulation
means that we can do work
with a bit, the smallest
unit
of
memory. Bit manipulations utilize
very small memory. Thus, we
can make an efficient
use of
the memory. The bit
fields are of great use in
operating systems and
files
attributes.
The bit manipulations are useful
while working at operating
system level.
Let's
have a look on different
operators, used for bit
manipulations.
Page
258
CS201
Introduction to Programming
Bit
Manipulation Operators
The
following table shows
different operators used for
bit manipulation.
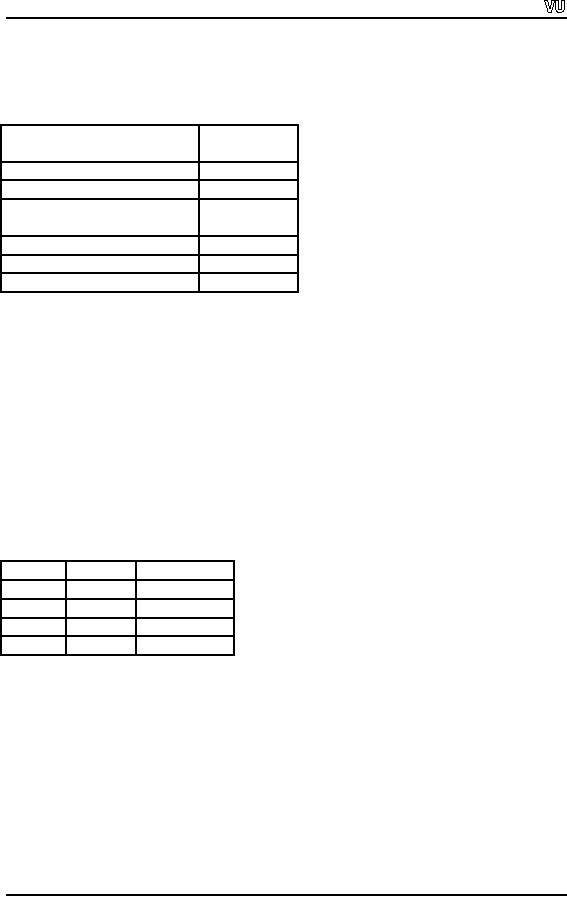
Operator
Operator
Sign
Bitwise
AND
Operator
&
Bitwise
OR
Operator
|
Bitwise
Exclusive
OR
^
Operator
NOT
Operator
~
Left
Shift Operator
<<
Right
Shift Operator
>>
Here & is
the bit-wise AND operator.
Don't confuse it with the
logical AND operator
&&.
Similarly | is the bit-wise OR
operator. Don't confuse it
with the logical OR
operator
||.
Now
let's talk about these
operators in detail.
AND
Operator ( & )
The AND
operator (&) works just
like the logical AND
operator (&&) but on bits.
It
compares
two bits and returns 1 if
both bits are 1. If any of
the two bits being
compared is
0, the
result will be 0.
Following
table, also called truth table,
will further explain the
operation of & operator.
Bit1
Bit2
Bit1
& Bit2
1
1
1
1
0
0
0
1
0
0
0
0
We know
that when a number is stored
in memory, it gets stored in
bit pattern which
has
binary
representation (only 1 and 0 ). So we
can use & to AND two
numbers bit-wise. To
understand
this, consider the following
example.
Suppose
we have two numbers - 12 and
8 and want to apply & on these
ones. Here we
will
make use of the binary
number system. The binary
representation (base 2 system)
of
12 and 8
are as 12 = (1100)2 and
8 = (1000) 2.
Now we apply the &
operator on these
numbers
and get the result as
follows
12
=
1
1
0
0
&
8=
1
0
0
0
Page
259

CS201
Introduction to Programming
-----------------------------
1
0
0
0
Thus 12
& 8 = (1000) 2
= 8. Don't
think 12 & 8 as an arithmetic
operation. It is just a
bit
manipulation
or a pattern matching issue. Each
bit of first number is
matched (compared)
with
corresponding bit of the
second number. The result of
& is 1 if both bits are
1.
Otherwise, it
will be 0. The & operator is
different from the &&
operator. The &&
operator
operates on two conditions (expressions)
and returns true or false
while the &
operator
works on bits (or bit
pattern) and returns a bit
(or bit pattern) in 1 or 0.
Example
1
We want
to determine whether in a number a
specific bit is 1 or 0. Suppose we
want to
determine
whether the fourth bit (i.e.
23) of a number is 1 or 0. We
will pick the
number
whose
fourth bit is 1 and the
remaining are zero. It is 23 (i.e. 8). Now we will
take AND
of the
given number with 8 (i.e
1000 in bit pattern.). In
bit manipulation, the number
is
written
in hexadecimal form. In the C language,
we put 0x or 0X before the
number to
write a
number in hexadecimal. Here we will write
8 as 0x8 in our code. Now
all the bits
of 8 are
zero except the fourth
one which is 1. The result
of the number being
ANDed
with 8
will be non-zero if the
fourth bit of the number is
1. As the fourth bit of 8 is
also 1,
& of
these two bits will
result 1. We call the result
non-zero just due to the
fact that we
are
not concerned with the
numbers like 1,2,3 or
whatsoever. We will write
this in the
form of a
statement as under
if
(number & 0x8)
instead
of if (
(number & ox8) >
=1)
The
if
looks
for a true or false. Any
non-zero value is considered
true and a zero is
considered
false. When we do bit-wise AND of two
numbers if the result is
non-zero (not
1 only,
it may be 1 or any other
number), this if
statement
will be true. Otherwise, it
will
be
false.
By a
non-zero value we simply
conclude that the fourth
bit of the number is set
(i.e. 1). A
bit is
said to be set in case it is 1
and `not set' if it is 0. This
way, we can set any
bit
pattern
in the power of 2, to determine whether a
specific bit of a number is
set or not.
For
example, to determine bit no. 3 of a
number we can AND it with 22 (4).
Following
is the code of the example
finding out whether the
fourth bit of a number is
set
(1) or
not set (0).
//This
program determines whether the
fourth bit of a number
entered by user is set or
not
#include
<iostream.h>
main()
{
int
number ;
cout
<< "Please enter a number "
;
cin
>> number ;
if
(number & 0x8 ) //8 is
written in hexadecimal form
cout
<< "The fourth bit of
the number is set" <<
endl;
Page
260
CS201
Introduction to Programming
else
cout
<< "The fourth bit of
the number is not set"
<< endl;
}
Sample
output of the program.
Please
enter a number 12
The
fourth bit of the number is
set
OR
Operator ( | )
The OR
operator, represented by `|'
works just like the &
operator with the
only
difference
that it returns 1 if any one
of the bits is 1. In other
words, it returns 0 only
if
both
the input bits are 0.
The | (bit-wise OR) operator
is different from the ||
(logical OR)
operator.
The || operator operates on
two conditions (expressions) and
returns true or false
while
the | operator works on bits
(bit pattern) and returns a
bit (or bit pattern) in 1 or
0.
The truth
table of OR operator is given
below.
Bit1
Bit2
Bit1
| Bit2
1
1
1
1
0
1
0
1
1
0
0
0
We can
make it sure that a specific
bit in a number should be 1
with the help of |
operator.
For
this purpose, we take OR of
this number with another
number whose bit pattern
has 1
in that
specific bit. Then OR will
produce 1 as the bit at that
position in second number
is
1 and OR
gives 1 if any one bit is
one. Thus in the output that
specific bit will have
1.
Let us
consider the following example in
which we apply OR operator on two
numbers
12 and
8.
12
=
1
1
0
0
|
8=
1
0
0
0
-----------------------------
1
1
0
0
Hence we
get 12 | 8 = 12.
In case,
x = 8 | 1, the OR operation will be as
under.
8=
1
0
0
0
|
1=
0
0
0
1
-------------------------
1
0
0
1
Page
261

CS201
Introduction to Programming
Thus x =
8 | 1 = 9.
Don't
take the statement in mathematical or
arithmetical terms. Rather
consider it from
the
perspective of pattern matching.
The &
operator is used to check whether a
specific bit is set or not
while the | operator
is
used to
set a specific bit.
Exclusive
OR Operator ( ^ )
Exclusive
OR operator uses the sign ^ .
This operator returns 1 when
one input is zero
and
the second is 1. It returns 0 if
both bits are same i.e.
both are either 0 or 1. The
truth
table of
exclusive OR, also called
xor (zor) , is given
below.
Bit1
Bit2
Bit1
^ Bit2
1
1
0
1
0
1
0
1
1
0
0
0
To
understand exclusive OR,
let's work out exclusive OR
of 8 and 1.
In the
following statement, the
pattern matching is shown for 8 ^
1.
8=
1
0
0
0
^
1=
0
0
0
1
-------------------------------
1
0
0
1
This
shows that 8 ^ 1 = 9. If we take again
exclusive OR of 9 with 1. The
result will be 8
again as
shown below.
9=
1
0
0
1
^
1=
0
0
0
1
----------------------------
1
0
0
0
While
taking ^ (exclusive OR) of a
number with a second number
and then ^ of the
result
with the second number, we
get the first number
again. This is a strength of
the ^
operator
that is very useful.
NOT
Operator ( ~ )
This is a
unary operator. It inverts the
bits of the input number,
meaning that if a bit
of
the
input number is 1, the
operator will change it to 0
and vice versa. The sign ~
is used
for
the NOT operator. Following
is the truth table of the
NOT operator.
Page
262

CS201
Introduction to Programming
Bit1
~
Bit1
1
0
0
1
Let's
take NOT of the number 8.
This will be as
follows
8=
1
0
0
0
Now ~8
will invert the bits
from 1 to 0 and from 0 to 1.
Thus ~8 will be
~8 =
0
1
1
1
which is
7.
The
bit manipulation operators
are very useful. Let's
consider some examples to see
the
usefulness
of these operators.
Example
(Bit Flags)
The
first example relates to operating
system. In Windows, you can
view the properties
of a
file. You can get
the option properties by
right clicking the mouse on
the file name in
any
folder structure. You will
see a window showing the
properties of the file. This
will
show
the name of the file,
the date of creation/modification of
the file etc. In the
below
part of
this window, you will
see some boxes with
check marks. These include read
only
and
archive etc. While looking at a
check mark, you feel of having a
look at a bit. If
there
is a
check mark, it means 1. Otherwise, it
will be 0. So we are looking at
bit flags which
will
depict the status of the
file. If the file is marked
read-only, a specific bit is
set to 1 in
the
operating system. This 1
indicates that the status of
the file is read-only.
When we
look for directory in UNIX
operating system, rwx, rx or rw
are seen before
the
name of a
file. The rwx are
actually symbols used for
read, write and execute
permissions
of the
file. These are the
attributes of the
file.
In
operating systems, the
attributes of a file are
best get as bit fields.
The 1 in a bit means
the
attribute is set and 0 means
the attribute is not set (or
cleared).
Example
(Masking)
Let's
see how ^ operator works.
Whenever you log on to a
system or server or to a
web
site
like yahoo or hotmail, you
enter your user name
and then the password.
The system
or server
validates your password and
allows the access. Your
password is kept in
the
database
of the system/server. When you
enter the password, the
system compares it
with
the
one earlier stored in its
database. If it matches, the
system allows you to access
the
system.
But there may be a problem at this
stage from the security
perspective. If the
password
is stored in the database as it is,
then the administrative (or
any person having
access to
database) can read the
password of any account. He
can make misuse of
password.
To prevent this and make the
password secure, most of the
operating systems
keep
the password in an encrypted fashion. It
codes the passwords to a
different bit
pattern
before storing it in its database so
that no body can read it.
Now when a user
enters
his password, there are two
methods to compare this
password with the
password
earlier
stored in the database.
Under the first method, on
entering the password,
the
password
stored will be decoded to
the original password and
compare with the
password
Page
263

CS201
Introduction to Programming
entered.
This is not a best way
because of two reasons. If
there is a method to decrypt a
password,
the administrator can decrypt the
password for any sort of
misuse. The second
method is
that when you enter a
password, it travels through
wires to go to somewhere
for
comparison. While it is traveling on
wire, someone can get
it. Another reason to
compare
the password in encrypted
form is that it is very easy
to do encryption but the
decryption
process is very difficult.
Therefore, to make this
process secure and easy,
the
password
entered is encrypted and
compared to the password in
the database, which
is
already
stored in encrypted
form.
The
Exclusive OR operator ( ^ ) can be
used to encrypt and decrypt
the password.
Suppose
there are two numbers
a
and
b. We take
c
= a ^ b. Now if
we take ^ of the result
c
with
b
(i.e.
c ^ b), the result will be
a.
Similarly, if we take Exclusive OR of
the result c
with
a
(c ^
a) , the answer will be b. You
can do exercise this
phenomenon by taking
any
values of
a
and
b. This
phenomenon of Exclusive OR can be
used to secure a
password.
You
can take Exclusive OR of the
password with a secret
number and save it to
the
database.
Now when it is needed to be
compared with entered
password, you again
take
Exclusive
OR of the saved password
with the same secret
number and get the
original
password
back. If someone else wants to
get the password, it is very
difficult for him/her
to get
that because the original
password will be got by
taking Exclusive OR of the
saved
password
with the same secret
number.
Here is
another example of Exclusive OR.
Sometimes, there are bad
sectors in a hard
disk,
which bring it to a halt. We cannot
access our data from
it. This is worst
situation.
In large
systems like servers, there
is a requirement that these
should work twenty
four
hours a
day, seven days a week. In
such systems, we cannot take
the risk. To avoid
this
and
meet the requirements, we
use a technique which is called
RAID. RAID stands
for
Redundant
Array of Inexpensive Devices. In this
technique, we use many disks
instead of
one.
Suppose we have nine disks.
Now when we say write a byte
on the disk, The
RAID
will
write a bit on first disk
then second bit on the
second disk and so on.
Thus 8 bits (one
byte) are
written on 8 disks. Now what
will be written on the ninth
disk? We take
exclusive
OR of these 8 bits pair by pair and
write the result on the
ninth disk. The
benefit of
this process that in case
one disk stops working, we
may place a new disk in
its
place.
And to write a bit on this
disk, we again take
Exclusive OR of eight bits on
the
other
disks and write the result
on this disk. This will be
the same bit that was
written in
the
damaged disk.
You
can prove it by the doing
the following exercise on
paper.
Write
eight bits, take their Exclusive OR one
by one and write it at ninth
position. Now
erase
any one bit and
take Exclusive OR of the remaining eight
bits. You will get
the
same
bit which was erased. Thus
it is a useful technique for recovering
the lost data
without
shutting down the system. We
replace the bad disk
with a new one while
the
system is
on. The system using
the RAID technique, writes
the data to the new
disk. This
technique
of replacing a disk is known as Hot
Plug.
We have
read the technique of swapping
two numbers. In this method,
we use a third
temporary
place to swap two numbers.
Suppose a
and
b
are to be
swapped. We store a
in
a temporary
place c. Then we
store b
in
a
and
put the value of c
(which
has the value of
a) in b. Thus
a
and
b
are
swapped.
Page
264

CS201
Introduction to Programming
We can
swap two numbers without
using a third place with
the help of Exclusive
OR.
Suppose
we want to swap two unsigned
numbers a
and
b.
These
can be swapped by the
following
three statements.
a=a^b;
b=b^a;
a=a^b;
Do
exercises of this swap
technique by taking different
values of a
and
b.
Unsigned
Integers
The
bit manipulations are done
with unsigned integers. The
most significant bit is used
as
a sign
bit. If this bit is zero,
the number is considered
positive. However, if it is 1,
the
number
will be considered negative.
Normally these bit manipulations
are done with
unsigned
integers. The unsigned
integers are declared
explicitly by using the
word
`unsigned' as
follow.
unsigned
int i, j, k ;
By this
declaration the integers i, j
and k will be treated as
positive numbers
only.
Sample
Program
The
following program demonstrate the
encryption and decryption of a password.
The
program
takes a password from user,
encrypts it by using Exclusive OR ( ^)
with a
number.
It displays the encrypted password.
Then it decrypts the
encrypted password
using
Exclusive OR ( ^ ) with the
same number and we get
the original password
again.
Following
is the code of the
program.
//This
program demonstrate the encryption by
using ^ operator
#
include<iostream.h>
main
()
{
char
password[10] ;
char
*passptr ;
cout
<< "Please enter a password(less
than 10 character): " ;
cin
>> password ;
passptr =
password ;
//now
encrypting the password by using ^
with 3
while
(*passptr != '\0' )
{
*passptr = (*passptr ^
3);
++passptr
;
}
cout
<< "The encrypted password is: "
<< password << endl;
//now
decrypting the encrypted password by
using ^ with 3
passptr =
password ;
Page
265
CS201
Introduction to Programming
while
(*passptr != '\0' )
{
*passptr = (*passptr ^
3);
++passptr
;
}
cout
<< "The decrypted password is: "
<< password << endl;
}
The
following is a sample output of the
program.
Please
enter a password(less than 10
character): zafar123
The
encrypted password is:
ybebq210
The
decrypted password is:
zafar123
Shift
Operators
Shifting
the binary numbers is
similar to shifting the
decimal numbers. Suppose we
have
1 in
decimal system and want to
shift it left in a way that
zero is put at the ending
place.
Thus 1
becomes 10. Mathematically, it is a
multiplication by 10. Now if we
shift 10 to
left
and place 0 at the last
place, we get 100. It is
again a multiplication by 10. In
pictorial
terms, we
can show this as
under.
1000
100
10
1
(In
decimal system)
0
0
0
1
The
value is 1
0
0
1
0
Shift
Left, The value is 10 (i.e.
multiplication by 10)
0
1
0
0
Shift
Left, The value is 100 (i.e.
multiplication by 10)
The
same thing applies when we
do bit shifts. If we shift a bit to
the left in the
binary
system,
it is multiplied by 2. If we do left
shift again we are
multiplying by 2 again.
Same
applies in the other direction. By
shifting to the right, we
will be dividing by 2 in
the
binary system and dividing by 10 in
decimal system. In this
process, the shifted
digit/bit
is discarded. When we do left shift,
zeroes are inserted in the
right side bits. The
same
applies to right shift, as
zeros are inserted in the
left side bits. But the
situation will
be
different if we use signed
numbers. As we know that in
signed numbers the
most
significant
bit is 1. Now you have to
see that what happens
while right shifting the
signed
number?
If zero is inserted at the
left most bit, the negative
number will become a
positive
number. Normally the
operating systems or compilers
treat it differently.
The
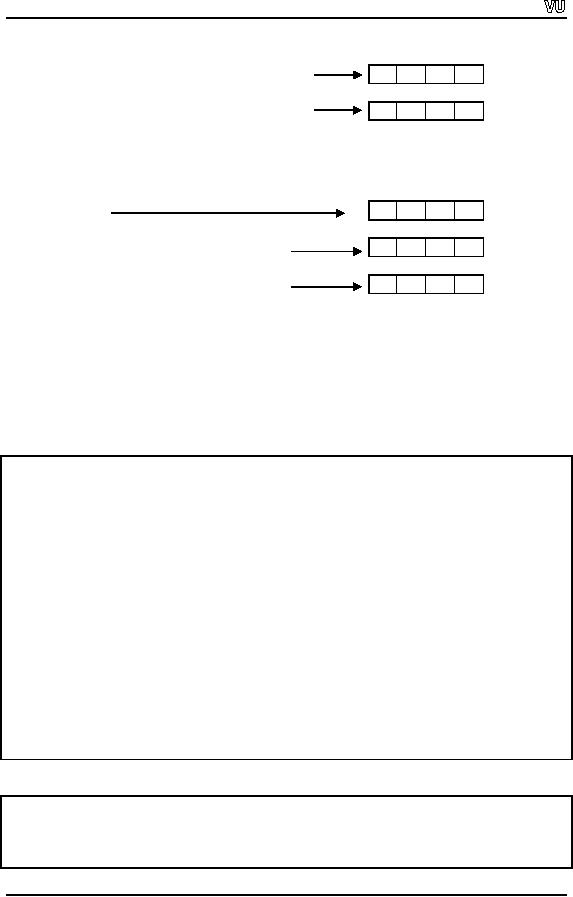
following figures show the
shift operations.
Shift
Left:
8
4
2
1
(In
binary system, bits
representation)
0
0
1
0
The
value is 2
Page
266
CS201
Introduction to Programming
Shift
Left , The value is 4 (i.e.
multiplication by 2)
0
1
0
0
Shift
Left, The value is 8 (i.e.
multiplication by 2)
1
0
0
0
Shift
Right:
8
4
2
1
(In
binary system, bits
representation)
1
1
0
0
The
value is 12
0
1
1
0
Shift
Right , The value is 6 (i.e.
division by 2)
0
0
1
1
Shift
Right, The value is 3 (i.e.
division by 2)
We have
specific operators for left
and right shifts. The left
shift operator is << and
right
shift
operator is >>. These
are the same signs as
used with cout
and
cin. But
these are
shift
operators. We can give a
number with these operators
to carry out shift operation
for
that
number of times. The following program
demonstrates the left and
right shift
operators.
//This
program demonstrate the left
and right shift
# include
<iostream.h>
main()
{
int
number, result ;
cout
<< "Please enter a number: "
;
cin
>> number ;
result =
number << 1 ;
cout
<< "The number after left
shift is " << result << endl
;
cout
<< "The number after left
shift again is " << (result << 1) <<
endl ;
cout
<< "Now applying right
shift" << endl ;
result =
number >> 1 ;
cout
<< "The number after right
shift is " << result <<
endl ;
cout
<< "The number after right
shift again is " << (result >> 1)
<< endl ;
}
Here is
the out put of the
program.
Please
enter a number: 12
The
number after left shift is
24
The
number after left shift
again is
48
Now
applying right shift
Page
267

CS201
Introduction to Programming
The
number after right shift is
6
The
number after right shift
again is
3
In the
output, we see that the left
shift operator (<<)
has multiplied the number by
2 and
the
right shift operator
(>>) has divided the
number by 2. The shift
operator is more
efficient
than direct multiplication and
division.
Exercises
· Write
different programs to demonstrate
the use of bit manipulation
operators.
· Write a
program which takes two
numbers, displays them in binary numbers
and then
displays
the results of AND, OR and
Exclusive OR of these numbers in
binary
numbers
so that operations can be
clearly understood.
· Write a
program which swaps two
numbers without using a temporary
third variable.
· Write a
program, which takes a
password from the user,
saves it to a file in
encrypted
form.
Then allow the user to
enter the password again
and compare it with the
stored
password
and show is the password
valid or not.
Page
268
Table of Contents:
- What is programming
- System Software, Application Software, C language
- C language: Variables, Data Types, Arithmetic Operators, Precedence of Operators
- C++: Examples of Expressions, Use of Operators
- Flow Charting, if/else structure, Logical Operators
- Repetition Structure (Loop), Overflow Condition, Infinite Loop, Properties of While loop, Flow Chart
- Do-While Statement, for Statement, Increment/decrement Operators
- Switch Statement, Break Statement, Continue Statement, Rules for structured Programming/Flow Charting
- Functions in C: Structure of a Function, Declaration and Definition of a Function
- Header Files, Scope of Identifiers, Functions, Call by Value, Call by Reference
- Arrays: Initialization of Arrays, Copying Arrays, Linear Search
- Character Arrays: Arrays Comparisonm, Sorting Arrays Searching arrays, Functions arrays, Multidimensional Arrays
- Array Manipulation, Real World Problem and Design Recipe
- Pointers: Declaration of Pointers, Bubble Sort Example, Pointers and Call By Reference
- Introduction, Relationship between Pointers and Arrays, Pointer Expressions and Arithmetic, Pointers Comparison, Pointer, String and Arrays
- Multi-dimensional Arrays, Pointers to Pointers, Command-line Arguments
- String Handling, String Manipulation Functions, Character Handling Functions, String Conversion Functions
- Files: Text File Handling, Output File Handling
- Sequential Access Files, Random Access Files, Setting the Position in a File, seekg() and tellg() Functions
- Structures, Declaration of a Structure, Initializing Structures, Functions and structures, Arrays of structures, sizeof operator
- Bit Manipulation Operators, AND Operator, OR Operator, Exclusive OR Operator, NOT Operator Bit Flags Masking Unsigned Integers
- Bitwise Manipulation and Assignment Operator, Programming Constructs
- Pre-processor, include directive, define directive, Other Preprocessor Directives, Macros
- Dynamic Memory Allocation, calloc, malloc, realloc Function, Dangling Pointers
- History of C/C++, Structured Programming, Default Function Arguments
- Classes and Objects, Structure of a class, Constructor
- Classes And Objects, Types of Constructors, Utility Functions, Destructors
- Memory Allocation in C++, Operator and Classes, Structures, Function in C++,
- Declaration of Friend Functions, Friend Classes
- Difference Between References and Pointers, Dangling References
- Operator Overloading, Non-member Operator Functions
- Overloading Minus Operator, Operators with Date Class, Unary Operators
- Assignment Operator, Self Assignmentm, Pointer, Conversions
- Dynamic Arrays of Objects, Overloading new and delete Operators
- Source and Destination of streams, Formatted Input and Output, Buffered Input/Output
- Stream Manipulations, Manipulators, Non Parameterized Manipulators, Formatting Manipulation
- Overloading Insertion and Extraction Operators
- User Defined Manipulator, Static keyword, Static Objects
- Pointers, References, Call by Value, Call by Reference, Dynamic Memory Allocation
- Advantages of Objects as Class Members, Structures as Class Members
- Overloading Template Functions, Template Functions and Objects
- Class Templates and Nontype Parameters, Templates and Static Members
- Matrices, Design Recipe, Problem Analysis, Design Issues and Class Interface
- Matrix Constructor, Matrix Class, Utility Functions of Matrix, Input, Transpose Function
- Operator Functions: Assignment, Addition, Plus-equal, Overloaded Plus, Minus, Multiplication, Insertion and Extraction