 |

CS201
Introduction to Programming
Lecture
Handout
Introduction
to Programming
Lecture
No. 13
Reading
Material
Deitel &
Deitel C++ How to
Program
Chapter
4
4.5,
4.9
Summary
�
Array
Manipulation
�
Real
World Problem and Design
Recipe
�
Exercises
Array
Manipulation
We have
already discussed what an
array is. Identical or similar
values are stored in
an
array.
The identical and similar
terms here are related to
the context of the problem
we
try to
solve. For example, height or age of an
individual is a number. We don't
store
height
and age in one array
as, in contextual terms, they
are different things. These
can
not be
mixed in one array. So the
height of individuals will be stored in
one array and
the
age in
some other one. The
idea behind the array is
that whenever you have
similar data
with
multiple values, it is easier
and more elegant to store them in an
array.
Let's
try to find out, how to
process arrays. What is the
easiest way and what
are the
issues
related to this
process.
As
discussed in previous lectures,
whenever we come across an
array, we start thinking
in
terms of
loops. We pick up the first
element of the array and
process it. Then the
second
array
element is processed and so
on. Naturally that falls
into an iterative structure.
Page
129

CS201
Introduction to Programming
Let's
try to understand how to
process a two dimensional array.
The following example
can
help us comprehend it
effectively.
Suppose
we have a two-dimensional array of
numbers. While dealing with a
two-
dimensional
array of numbers, we should
try to understand it in terms of a
matrix.
Matrices
in mathematics have rows and
column and there is always a
number at each row
and
column intersection. Suppose we have a
matrix of dimension 3 * 3 i.e. a simple
two-
dimensional
array. We want to input some
numbers to that array first.
After reading these
numbers,
we want to output them in such a fashion
that the last row is printed
first,
followed
by second last and so on
till the first row
that is printed at the bottom. We
don't
want to
change the column numbers
with this output. It is not a
difficult task. As it is a
two-dimensional
array so there is a row
subscript and a column
subscript. Following
example
will make the matter further
clear.
Suppose
we have the following
array:
int
a[3][3];
We will
access elements of it as:
a[row index][column index]
e.g. a[1][2]. This is a
single
element
at row 1 and column 2 of
array a.
The
flow chart to read in
numbers into the
two-dimensional array is given on the
next
page.
See the code snippet
below:
const
int maxRows = 3;
const
int maxCols = 3;
int
row, col;
int
a[maxRows][maxCols];
// To
input numbers in the
array
for
(row = 0; row < maxRows;
row ++)
{
for(col=0;
col < maxCols; col
++)
{
cout
<< "\n" << "Enter " <<
row << "," << col <<
"element: ";
cin
>> a[row][col];
}
}
Now
let's see what this
nested loop structure is doing.
The outer loop takes
the first row
i.e. row
0, then instantly inner loop
begins which reads col 0, 1
and 2 elements of the
row
0 into
the array. Afterwards,
control goes back to the
outer loop. The row
counter is
incremented
and becomes 1 i.e. row 1 or
second row is taken for
processing. Again,
the
inner
loop reads all the
elements of second row into
the array. This process
goes on until
all
the elements for three
rows and three columns array
are read and stored in
the array
called a.
Page
130
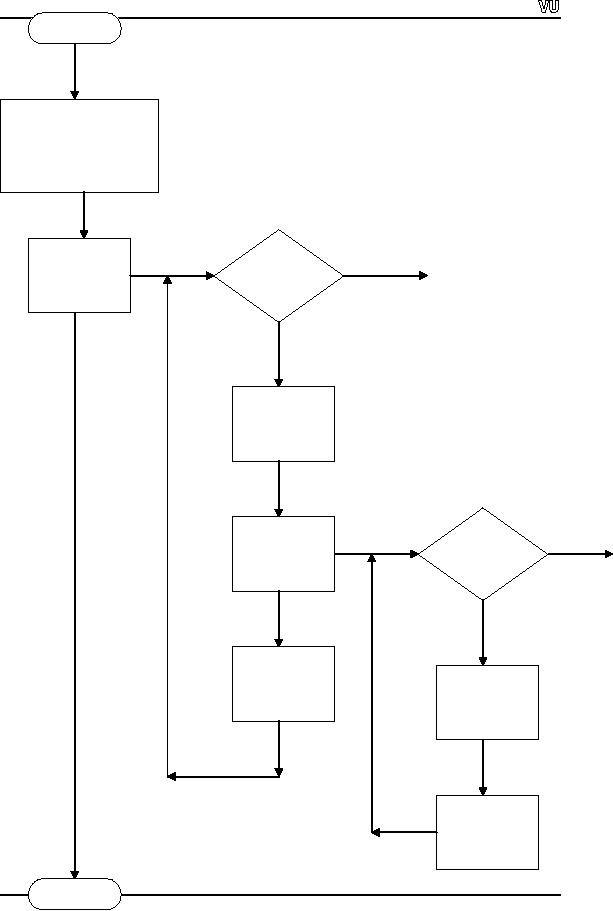
CS201
Introduction to Programming
Flow
Chart to Input Two-dimensional
Array
maxRows =
n
maxCols =
n
a[maxRows][maxCol
s]
No
row
<
while
Exit
maxRows
Yes
col =
0
No
col
<
while
Exit
maxCols
Yes
row++
Read
a[row][col]
col++
Page
131

CS201
Introduction to Programming
Now we
want to reverse the rows of
the matrix (flip the
matrix) and display it.
There are
several
ways of doing it. You might
have already started
thinking of how can we flip
the
matrix.
We may declare a new matrix
and copy the array elements
into this matrix
while
flipping
the elements at the same
time. But we should keep in
mind the problem
statement.
The problem statement is 'to read
the array elements and
then simply display it
in the
reverse row order'. It does
not state anything about storing
the elements inside
the
memory.
Please
see the flow chart to
display the flipped matrix on
the next page.
Normally,
we start our loops from
zero and keep incrementing
the counter until a
certain
bigger
value is attained. But this
is not mandatory. We can start
from a bigger number
and
keep on decrementing the
counter every time. To
display the rows in reverse
order,
we can
start from the last
row and go to the first
row by decrementing the row
counter
every
time. It is very simple programming
trick. However, we have to
take care of the
value of
the index.
We can
write our code inside nested
loops for flipping the
elements as under-
// To
flip the elements of the
matrix
cout
<< '\n' << "The flipped
matrix is: " << '\n';
for (
row = maxRows-1; row >= 0;
row --)
{
for (
col = 0; col < maxCols;
col ++)
{
cout
<< a [row][col] << '\t';
}
cout
<< '\n';
}
Note
the '\t' character in the
above code. It is a tab
character that displays tab
(spaces) at
the
cursor position on the
screen. Similary '\n' as
told in previous lectures is
newline
character
which takes the cursor to
the new line.
It is
better to print the original
matrix elements before
showing the flipped
matrix
elements
so that you can really
see whether your function
has flipped the matrix or
not.
To run
this function for the
big-sized arrays, adjust the
values of the maxRows
and
maxCols
constants as the rest of the
program remains the
same..
Whenever
we work with arrays,
normally the loops are
there. If the array is
single
dimensional,
there will be one loop. A
two-dimensional arrays is going to have
pair of
nested
loops and so on.
Page
132
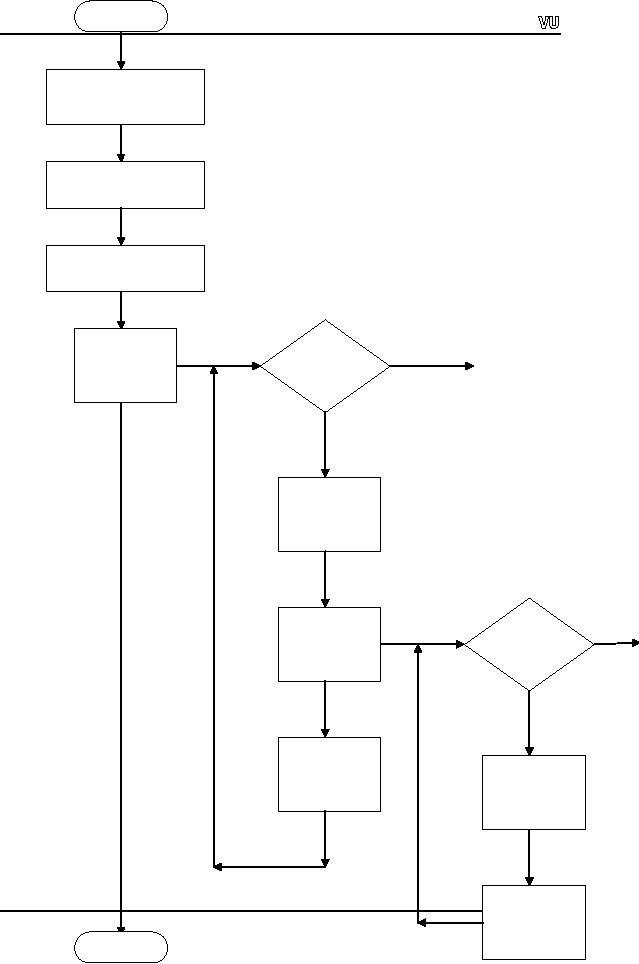
Flow
Chart to
Display Array Elements in
the Reverse
CS201
Introduction to Programming
Row
Order
maxRows =
n
maxCols =
n
a[maxRows][maxCol
Input
the array `a'
elements
row =
maxRows - 1
No
while
row >=
0
Exit
Yes
col =
0
No
col
<
while
Exit
maxCols
Yes
row--
Print
a[row][col]
Page
133
col++

CS201
Introduction to Programming
/* Array
Manipulation - Flipping of a Matrix
(reversing the row order):
This program reads a
matrix
(two-dimensional array), displays its
contents and also displays
the flipped matrix
*/
#include
<iostream.h>
const
int maxRows = 3;
const
int maxCols = 3;
void
readMatrix(int arr[][maxCols]);
void
displayMatrix(int a[][maxCols]);
void
displayFlippedMatrix(int
a[][maxCols]);
void
main(void)
{
int
a[maxRows][maxCols];
// Read
the matrix elements into
the array
readMatrix(a);
//
Display the original
matrix
cout
<< "\n\n" << "The original
matrix is: " << '\n';
displayMatrix(a);
//
Display the flipped
matrix
cout
<< "\n\n" << "The flipped
matrix is: " << '\n';
displayFlippedMatrix(a);
}
void
readMatrix(int arr[][maxCols])
{
int
row, col;
for
(row = 0; row < maxRows;
row ++)
{
for(col=0;
col < maxCols; col
++)
{
cout
<< "\n" << "Enter " <<
row << ", " << col << " element:
";
cin
>> arr[row][col];
}
cout
<< '\n';
Page
134

CS201
Introduction to Programming
}
}
void
displayMatrix(int a[][maxCols])
{
int
row, col;
for
(row = 0; row < maxRows;
row ++)
{
for(col =
0; col < maxCols; col
++)
{
cout
<< a[row][col] << '\t';
}
cout
<< '\n';
}
}
void
displayFlippedMatrix(int
a[][maxCols])
{
int
row, col;
for
(row = maxRows - 1; row >= 0;
row --)
{
for(col =
0; col < maxCols; col
++)
{
cout
<< a[row][col] << '\t';
}
cout
<< '\n';
}
}
Page
135

CS201
Introduction to Programming
Till
now, we have only solved
very simple problems to understand
processing of arrays.
You
can test your capability of
doing so through an exercise by inputting
(reading in) a
matrix
and print it in reverse
column order. Here, the rows
remain the same.
Let's
move on to slightly more practical problem. Before
going ahead, we need to
understand
the concept of Transpose of a
Matrix. Transpose of a matrix
means that when
we
interchange rows and columns,
the first row becomes
the first column, second
row
becomes
the second column and so
on. Mathematically, the
transpose can be written
as:
A(i,j)
should be replaced with
A(j,i) where i and j are row
and column indexes.
For
this purpose, we take a
square matrix (a matrix with
equal number of rows
and
columns) to
transpose. Here, if you are
thinking in terms of loops,
you are absolutely
right.
Let's say the array is
'a', with dimension as `arraySize'.
Please see the flow
chart for
this
problem on the next
page.
We write
a pair of nested loops:
int
temp;
for
(row = 0; row < arraySize; row
++)
{
for
(col = 0; col < arraySize; col
++)
{
//
Interchange the values here
using the swapping mechanism
temp =
a[row][col]; // Save the
original value in the
temp
variable
a[row][col]
= a[col][row];
a[col][row]
= temp; //Take out the
original value
}
}
While
interchanging values, we should be careful. We
can't simply write:
a[row][col] =
a[col][row].
We will lose information
this way. We need a swapping mechanism
here to
interchange
the elements properly.
We have
yet to do more to get the problem solved.
You are strongly recommended
to
write
this program and run it to
see the problem
area.
It is something
interesting that we are interchanging the
value of first row, first
column
with
itself, which means nothing. When we
are doing transpose of a matrix,
the diagonal
elements
will remain unchanged as the
row and column indexes
are the same. Then
we
interchange
the row 0, col 1 element
with row 1, col 0. The
row 0, col 2 element with
row
2, col 0.
What will happen when we
process second row i.e. row
1. The row 1, col 0
will
be
swapped with row 0, col 1
but these are the
same elements, already
swapped in the
above
iteration. Therefore, this is the
problem area that elements
swapped once are
Page
136
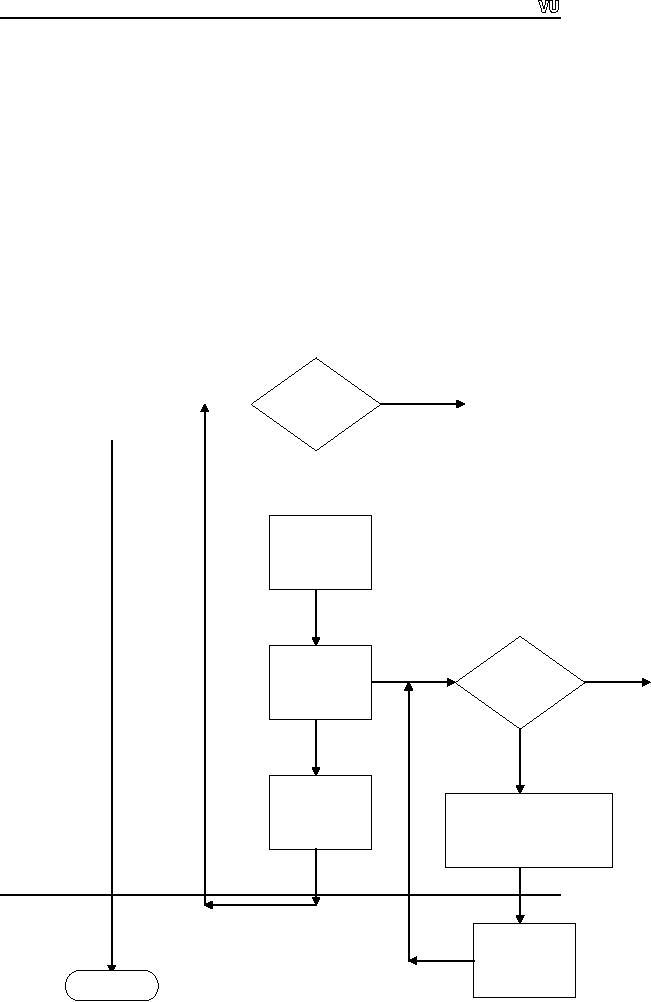
CS201
Introduction to Programming
swapped
again to their original positions if
the loops are run in
all the rows and
columns.
As a
result, the resultant matrix
remains unchanged.
No
row
<
arraySize
Yes
col =
row
No
col
<
while
arraySize
Yes
row++
temp =
a[row][col]
a[row][col]
=
a[col][row]
a[col][row]
= temp
Page
137
col++
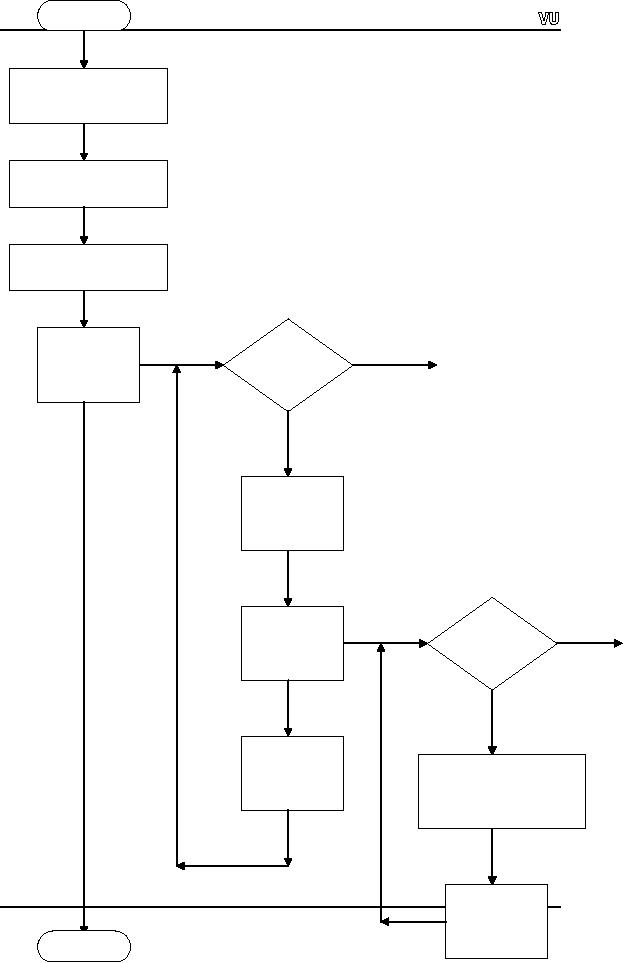
CS201
Introduction to Programming
Flow
Chart
of Transpose
of a Square Matrix
arraySize =
n
a[arraySize][arraySiz
]
Input
the array `a'
elements
row =
0
No
row
<
Exit
while
arraySize
Yes
col =
row
No
col
<
Exit
while
arraySize
Yes
row
++
temp =
a[row][col]
a[row][col]
=
a[col][row]
[
l][
]t
Page
138
col++

CS201
Introduction to Programming
Then
what is the solution of the
problem?
Now
draw a matrix on the paper
and cut it diagonally. We will
get two triangles i.e.
upper
triangle
and lower triangle. We only
need to interchange one triangle
with the other
and
not
the whole of the matrix.
Now the question is, how we
can determine the limits
of
triangles?
By looking at a triangle, let's say
upper triangle, we can see
that all the
rows
are
being processed as the triangle
crosses every row. Similarly
all the columns are
being
processed
because the first row in
the upper triangle covers
all the columns. The
only
difference is
that we will not process
the beginning element before starting
each row.
That
means that we will not
start the inner loop (columns
loop) with index 0. Rather
we
start
with the current row
number. Therefore, for first
row i.e. row 0, we will
process
from
row 0, col 0 to row 0, col
arraySize-1. For second row i.e.
row 1, we will
process
from
row 1, col 1 to row 1, col
arraySize-1 while in case of third
row i.e. row 2, we
will
go from
row 2, col 2 to row 2 , col
arraySize-1. If you structure the
loops in this manner,
the
correct behavior of matrix transposition
will be found.
The
full source code to solve
this problem by taking the
upper triangle and swapping it
with
the lower triangle is given
below:
/*
Array Manipulation - Transpose of a
Square Matrix: This program
reads a matrix (two-
dimensional
array), displays its contents,
transposes it and then displays
the transposed
matrix.
*/
#include
<iostream.h>
const
int arraySize = 3;
void
readMatrix(int arr[][arraySize]);
void
displayMatrix(int a[][arraySize]);
void
transposeMatrix(int
a[][arraySize]);
void
main(void)
{
int
a[arraySize][arraySize];
// Read
the matrix elements into
the array
readMatrix(a);
//
Display the matrix
cout
<< "\n\n" << "The original
matrix is: " << '\n';
displayMatrix(a);
//Transpose
the matrix
transposeMatrix(a);
Page
139

CS201
Introduction to Programming
//Display
the transposed matrix
cout
<< "\n\n" << "The transposed
matrix is: " << '\n';
displayMatrix(a);
}
void
readMatrix(int arr[][arraySize])
{
int
row, col;
for
(row = 0; row < arraySize; row
++)
{
for(col=0;
col < arraySize; col
++)
{
cout
<< "\n" << "Enter " <<
row << ", " << col << " element:
";
cin
>> arr[row][col];
}
cout
<< '\n';
}
}
void
displayMatrix(int a[][arraySize])
{
int
row, col;
for
(row = 0; row < arraySize; row
++)
{
for(col =
0; col < arraySize; col
++)
{
cout
<< a[row][col] << '\t';
}
cout
<< '\n';
}
}
void
transposeMatrix(int a[][arraySize])
{
int
row, col;
int
temp;
for
(row = 0; row < arraySize; row
++)
{
Page
140

CS201
Introduction to Programming
for
(col = row; col < arraySize;
col ++)
{
/*
Interchange the values here
using the swapping mechanism */
temp =
a[row][col];
// Save
the original value in the
temp variable
a[row][col]
= a[col][row];
a[col][row]
= temp;
//Take
out the original
value
}
}
}
Page
141

CS201
Introduction to Programming
Real
Word Problem and Design
Recipe
We will
take one problem that is
not very complex but
will follow it rigorously
for all
steps of
design recipe.
In practical
life, the employees get
salaries and pay taxes
honestly. Sometimes, the
process
of drawing salaries and
payment of taxes may lead to
some interesting situation.
Suppose,
a person draws salary of Rs.
10,000 per month. A certain
percentage of tax is
charged
on that amount, which is
deducted every month. But if
the salary of the person
is
more than
Rs. 10,000 per month, then
the tax rate is different.
Similarly if a person is
getting
Rs. 20,000 per month, he/she
would be charged more under a
different tax rate
slab.
The interesting situation develops if
there is an anomaly in the tax
rates i.e. a person
who is
getting higher salary takes home
lesser money as compared to the
other person
with
less gross salary.
To further
elaborate it, we suppose
that there is company 'C' where 100 or
less than 100
persons
are employed. The salaries of
the employees and their tax
rates are known to
us.
We are
required to list those
unlucky persons, who are
getting lesser take-home
salary
(net
salary) than their colleagues
with less gross salaries
but lower tax
rates.
As per
our design recipe, let's
see what steps we need to
follow.
A design
recipe asks us to analyze
the problem first and write
it in a precise statement
that
what actual the problem is.
Also by formulating the
precise statement, we need
to
provide
some examples to illustrate. At the
design phase, we try to
break up the problem
into
functional units and resort to a
detailed designing. Then we
move to implementation
stage
where the pseudo code is
translated into the computer
language and then
the
program
is compiled and run to
ensure that it works as
expected.
At the
first step i.e Analysis, we
try to have a precise problem
statement. Once it is
established,
we try to determine what are
the inputs of this program.
What data should be
provided to
this program. We will also
try to determine if there
are some constants
required
for calculation or manipulation. We list
down all the constants.
Then we split it
up into
functions and modules.
Let's
try to make a precise
statement of the above problem.
The precise problem
statement
is:
"Given
tax brackets and given
employees gross salaries,
determine those employees
who
actually
get less take-home salary
than others with lower
initial income."
Suppose
the tax deduction law
states that:
Page
142

CS201
Introduction to Programming
-
No tax
will be deducted for persons
with salaries ranging from
Rs. 0 to Rs. 5,000
per
month or
in other words tax deduction
rate is 0%.
-
5% tax
deduction will be made from
the persons with salaries
ranging from Rs.
5,001
to Rs.
10,000 per month.
-
For
persons with salaries
ranging from Rs. 10,001 to
Rs. 20,000, a 10% tax
deduction
rate
would be employed.
-
For
persons with salaries
ranging from Rs. 20,001
and higher, 15% tax
deduction
would be
made.
Taking
these rules, let's formulate
the problem.
Consider
the example of a person with a
salary of Rs. 10,000 per
month. As per rules,
he/she
would be charged by 5% of tax
rate. 5% of 10,000 is 500
rupees. So the take
home
salary of
the person is Rs.
9500.
Now
the unfortunate individual,
whose gross salary is Rs,
10,001 falls in the next
bracket
of tax
rate of 10%. He will have to
pay tax worth Rs 1000.1.
That means the take
home
salary of
this person is Rs. 9000.9,
which is lesser than the
person with lower gross
salary
of Rs.
10,000. This is the
problem.
We can
calculate the net salaries
of all individuals, determining all
the unlucky ones.
Now we
will carry out the analysis
of the requirements. For
looking into the
requirements,
we have to see, how to input
the salaries of these
people.
As stated
in the problem, the number of
employees of the company 'C is at most
100. So
we know
the size of the array. But
for some other company,
suppose company 'D', we
don't
know the number of
employees. Therefore, it makes
sense to take input from
the
user
for the number of employees.
Once we have determined the
number of employees,
we will
input the gross salary of
each of employees. But where
will we store the
gross
salary?
For this purpose, we will
use the two-dimensional
array. In the first column,
we
will
store the gross salary. Our
program after calculating the net
salary for each
employee
will
write (store) it in the
second column of the
array.
At the
next stage, we will find
out the unlucky individuals.
This will be based on
the
analysis
of algorithms. At the higher level
design, we assume that there
would be a way
to
determine the unlucky
individuals. Finally, a list of
unlucky employees would
be
prepared.
For that, we will simply
output the employee
numbers.
We want
to workout the space and
storage requirements of this problem. As
earlier
mentioned, we
will use a two dimensional
array to store the gross
and net salaries
and
output
the list of unlucky
employees. That means we
need a storage to store that
list. For
this, we
will take a single dimensional array of
'int' type. We will initialize
the array with
zero.
'0' means the individual is
lucky. Therefore, by default, all
individuals are
lucky.
Whenever,
we will find an unlucky
individual by using the two
dimensional array, we
will
write '1' in single dimensional array
for that individual. So this
is the storage
requirement
of the program.
Afterwards,
we will discuss the
interface issues. The
interface guidelines are the
same i.e.
be polite
and try to explain what is
required from the user. When
the program runs
the
user
will know what is required
from him/her. So there would
be prompts in the program
Page
143

CS201
Introduction to Programming
where the
user will key in the
data. All the input data
will be coming from keyboard
and
displayed on
the screen. This is a rudimentary
interface analysis.
We have
distributed the program into
four major parts:
1.
Input
2. Salary
calculation
3.
Identification of unlucky individuals
and
4.
Output
Let's
start the coding or detailed
design phase of this
program.
In a true
tradition, all the four
parts of the program should
be function calls. The
main
program
is very simple as it contains
functions:
-
Get
input
-
Calculate
salary
-
Locate
unlucky individuals
-
Display
output
The
arrays will be declared inside
the main function. As we
already know the
maximum
number of
employees is 100, so we can
declare it as a constant:
const
int arraySize=100;
double
sal[arraySize][2];
int
lucky[arraySize] = {0};
//Notice
the array
initialization
Once
this is done inside main, we
want to run the input
function to read the
salaries of the
employees.
Now, inside the input data
function, we will get value
for number of
employees
from the user. We have
already set the upper
limit as 100 but the
actual
number of
employees will be entered by
the user of the program. If we
take that input
inside
the input data function,
what can be the problem.
Well, there is no problem in
taking
the input within that
function but the problem is
the declaration of the
variable
'numEmps',
which contains the current
number of employees. If the 'numEmps'
variable
is
declared inside the input
data function, it will be
local to that function.
After the input
data
function returns, the 'numEmps'
will no longer be there because it was
local to input
data
function and not visible in
any other function. So it is
better to declare the
variables
inside
the main function. But
the problem arises: how the
input data function will
get
information
about it, if we declare it inside
main function. We will have
to send it to
input
data function, either
through call by reference or we
can declare 'numEmp' as
a
global
variable so that it is visible in all
the functions. Global variables
are useful but
tricky.
They exist when we need them
but they exist even
when we don't need
them.
Therefore,
it might be good to declare
this variable 'numEmps' inside main
function and
then
pass by reference to the
input data function.
Page
144

CS201
Introduction to Programming
While
passing one-dimensional array to the
function, we write in the
function prototype
as:
f(int
a[]);
However,
when we pass two-dimensional
array to a function, we must specify
the
number of
columns because this depends on
how a computer stores the
two dimensional
array in
the memory. The computer
stores the rows in a
contiguous (row after
row)
fashion inside
memory. Therefore , in order to
locate where the first row
has finished or
the
second row starts, it should
know the number of columns.
Whenever, we pass
two-
dimensional
array to a function, the
number of columns inside that array
should be
specified. We
will pass two dimensional
array 'sal' to input data
function getInput() in the
same
manner. We also want to pass
'numEmps' variable by reference using the
'&' sign to
this
function. This will ensure
that whatever the user inputs inside
this function
getInput(),
will be available in the main
function. There is another
way that we get
input
from
the user inside the main
function and then pass
this by value to the
getInput()
function.
We are going to do the same in
our function.
getInput(double
sal[][2], int
numEmps);
{
for
(int i = 0; i < numEmps; i ++)
//Note that this numEmps is
local to this
function
{
cin
>> sal[i][0];
// Get
the gross salary for
each
employee
}
}
To
calculate tax, we will write
a function. This function
will be passed in
similar
parameters
as getInput function to calculate the
taxes for all the
employees. There is
one
important
point to reiterate here i.e. by default,
arrays are passed by
reference. That
means if
getInput()
function
puts some values in the
'sal' array, these are
written in the
'sal'
array and are available inside
main function. The 'numEmps' variable on
the other
hand is
passed by value to getInput() function.
Therefore, any changes done
by geInput()
function
will not affect the original
value of 'numEmps' inside the main
function.
We will
continue with this problem
to determine algorithm that
what is the precise
sequence
of steps to determine the
unlucky employees. For this, we
need to analyze a bit
more
because it contains a complex
'if' condition. The function
to calculate net salary
also
has
interesting issues which will be
explained in the next
lecture.
Here is
the source code of the
first cut solution for real
world problem:
* This is
the first cut of the program
to solve the real world
problem of
'Unlucky
Employees' */
Page
145

CS201
Introduction to Programming
#include
<iostream.h>
void
getInput(double sal[][2], int
numEmps);
void
calcNetSal(double sal[][2], int
numEmps);
void
findUnluckies(double sal[][2], int
numEmps, int lucky[]);
void
markIfUnlucky(double sal[][2], int
numEmps, int lucky[], int
upperBound, int
empNbr);
void
printUnluckies(int lucky[], int
numEmps);
void
main(void)
{
const
int arraySize=100;
double
sal[arraySize][2];
int
lucky[arraySize] = {0};
int
numEmps;
/* Read
the actual number of
employees in the company */
cout
<< "\n Please enter
the total number of
employees in your company: ";
cin
>> numEmps;
cout
<< '\n';
/* Read
the gross salaries of the
employees into the array
'sal' */
getInput(sal,
numEmps);
/* Calculate
net salaries of the
employees and store them in
the array */
cout
<< "\n\n Calculating the
net salaries ... ";
calcNetSal(sal,
numEmps);
/* Find
the unlucky employees
*/
cout
<< "\n\n Locating the
unlucky employees ...
";
findUnluckies(sal,
numEmps, lucky);
/* Print
the unlucky employee numbers
*/
cout
<< "\n\n Printing the
unlucky employees ...
";
printUnluckies(lucky,
numEmps);
}
void
getInput(double sal[][2], int
numEmps)
{
for
(int i = 0; i < numEmps; i++)
//Note that this numEmps is
local to this
function
{
cout
<< "\n Please enter
the gross salary for
employee no." << i << ":
";
cin
>> sal[i][0];
// Store
the gross salary for
each employee
}
}
Page
146

CS201
Introduction to Programming
void
calcNetSal(double sal[][2], int
numEmps)
{
for
(int i = 0; i < numEmps; i++)
//Note that this numEmps is
local to this
function
{
if(sal[i][0]
>= 0 && sal[i][0] <=
5000)
{
/* There
is no tax deduction */
sal[i][1]
= sal[i][0];
}
else
if(sal[i][0] >= 5001 &&
sal[i][0] <= 10000)
{
/* Tax
deduction is 5% */
sal[i][1]
= sal[i][0] - (.05 *
sal[i][0]);
}
else if
(sal[i][0] >= 10001 &&
sal[i][0] <= 20000)
{
/* Tax
deduction is 10% */
sal[i][1]
= sal[i][0] - (.10 *
sal[i][0]);
}
else if
(sal[i][0] >= 20001)
{
/* Tax
deduction is 15% */
sal[i][1]
= sal[i][0] - (.15 *
sal[i][0]);
}
else
{
/* No
need to do anything here */
}
}
}
void
findUnluckies(double sal[][2], int
numEmps, int lucky[])
{
for
(int i = 0; i < numEmps; i++)
//Note that this numEmps is
local to this
function
{
if(sal[i][0]
>= 0 && sal[i][0] <=
5000)
{
/* No
need to check for unlucky
employees for this tax
bracket */
;
}
else
if(sal[i][0] >= 5001 &&
sal[i][0] <= 10000)
{
markIfUnlucky(sal,
numEmps, lucky, 5001,
i);
}
else if
(sal[i][0] >= 10001 &&
sal[i][0] <= 20000)
{
Page
147

CS201
Introduction to Programming
markIfUnlucky(sal,
numEmps, lucky, 10001,
i);
}
else if
(sal[i][0] >= 20001)
{
markIfUnlucky(sal,
numEmps, lucky, 20001,
i);
}
}
}
void
markIfUnlucky(double sal[][2], int
numEmps, int lucky[], int
upperBound, int
empNbr)
{
for
(int i = 0; i < numEmps;
i++)
{
/*
See
the if the condition below,
it will mark the
employee
unlucky
even if an employee in the higher
tax bracket is getting
the
same amount of net salary as
that of a person in the
lower
tax
bracket
*/
if
(sal[i][0] < upperBound &&
sal[i][1] >= sal[empNbr][1])
{
lucky[empNbr]
= 1;
//Employee
marked as unlucky
break;
}
}
}
void
printUnluckies(int lucky[], int
numEmps)
{
for
(int i = 0; i < numEmps;
i++)
{
if(lucky[i]
== 1)
{
cout
<<"\n Employee No.: " <<
i;
}
}
}
Exercises
1.
Suppose you have a Square
matrix of order 5 * 5. Draw
flow chart and write
a
program to
input (read in) a matrix
and print it in reverse
column order, the
rows
remain
the same.
Page
148

CS201
Introduction to Programming
2.
Suppose you have a Square
matrix of order 5 * 5. Draw
flow chart and write
a
program to
transpose the matrix, take
lower triangle and swap it
with upper
triangle.
3. An
Identity matrix is a square
matrix whose diagonal
elements are '1'
and
remaining
elements are '0'. Suppose
you are given a square
matrix of size n * n.
Write a
program to determine if this is an
Identity matrix.
Page
149
Table of Contents:
- What is programming
- System Software, Application Software, C language
- C language: Variables, Data Types, Arithmetic Operators, Precedence of Operators
- C++: Examples of Expressions, Use of Operators
- Flow Charting, if/else structure, Logical Operators
- Repetition Structure (Loop), Overflow Condition, Infinite Loop, Properties of While loop, Flow Chart
- Do-While Statement, for Statement, Increment/decrement Operators
- Switch Statement, Break Statement, Continue Statement, Rules for structured Programming/Flow Charting
- Functions in C: Structure of a Function, Declaration and Definition of a Function
- Header Files, Scope of Identifiers, Functions, Call by Value, Call by Reference
- Arrays: Initialization of Arrays, Copying Arrays, Linear Search
- Character Arrays: Arrays Comparisonm, Sorting Arrays Searching arrays, Functions arrays, Multidimensional Arrays
- Array Manipulation, Real World Problem and Design Recipe
- Pointers: Declaration of Pointers, Bubble Sort Example, Pointers and Call By Reference
- Introduction, Relationship between Pointers and Arrays, Pointer Expressions and Arithmetic, Pointers Comparison, Pointer, String and Arrays
- Multi-dimensional Arrays, Pointers to Pointers, Command-line Arguments
- String Handling, String Manipulation Functions, Character Handling Functions, String Conversion Functions
- Files: Text File Handling, Output File Handling
- Sequential Access Files, Random Access Files, Setting the Position in a File, seekg() and tellg() Functions
- Structures, Declaration of a Structure, Initializing Structures, Functions and structures, Arrays of structures, sizeof operator
- Bit Manipulation Operators, AND Operator, OR Operator, Exclusive OR Operator, NOT Operator Bit Flags Masking Unsigned Integers
- Bitwise Manipulation and Assignment Operator, Programming Constructs
- Pre-processor, include directive, define directive, Other Preprocessor Directives, Macros
- Dynamic Memory Allocation, calloc, malloc, realloc Function, Dangling Pointers
- History of C/C++, Structured Programming, Default Function Arguments
- Classes and Objects, Structure of a class, Constructor
- Classes And Objects, Types of Constructors, Utility Functions, Destructors
- Memory Allocation in C++, Operator and Classes, Structures, Function in C++,
- Declaration of Friend Functions, Friend Classes
- Difference Between References and Pointers, Dangling References
- Operator Overloading, Non-member Operator Functions
- Overloading Minus Operator, Operators with Date Class, Unary Operators
- Assignment Operator, Self Assignmentm, Pointer, Conversions
- Dynamic Arrays of Objects, Overloading new and delete Operators
- Source and Destination of streams, Formatted Input and Output, Buffered Input/Output
- Stream Manipulations, Manipulators, Non Parameterized Manipulators, Formatting Manipulation
- Overloading Insertion and Extraction Operators
- User Defined Manipulator, Static keyword, Static Objects
- Pointers, References, Call by Value, Call by Reference, Dynamic Memory Allocation
- Advantages of Objects as Class Members, Structures as Class Members
- Overloading Template Functions, Template Functions and Objects
- Class Templates and Nontype Parameters, Templates and Static Members
- Matrices, Design Recipe, Problem Analysis, Design Issues and Class Interface
- Matrix Constructor, Matrix Class, Utility Functions of Matrix, Input, Transpose Function
- Operator Functions: Assignment, Addition, Plus-equal, Overloaded Plus, Minus, Multiplication, Insertion and Extraction