 |
Cameras:LINEARITY, Absolute sensitivity, Relative sensitivity, PIXEL FORM |
| << Noise:PHOTON NOISE, THERMAL NOISE, KTC NOISE, QUANTIZATION NOISE |
| Displays:REFRESH RATE, INTERLACING, RESOLUTION >> |
...Image
Processing Fundamentals
signal
readout and is thus independent of
the integration time (see
Sections 6.1 and
7.7).
Proper electronic design
that makes use, for example,
of correlated double
sampling
and dual-slope integration
can almost completely
eliminate KTC noise
[22].
6.5
AMPLIFIER NOISE
The
standard model for this type
of noise is additive, Gaussian, and independent
of
the
signal. In modern well-designed
electronics, amplifier noise is
generally
negligible.
The most common exception to
this is in color cameras where
more
amplification
is used in the blue color
channel than in the green
channel or red
channel
leading to more noise in the
blue channel. (See also
Section 7.6.)
6.6
QUANTIZATION NOISE
Quantization
noise is inherent in the amplitude
quantization process and occurs
in
the
analog-to-digital converter, ADC.
The noise is additive and independent of
the
signal
when the number of levels L
≥ 16.
This is equivalent to B
≥ 4
bits. (See
Section
2.1.) For a signal that
has been converted to
electrical form and thus has
a
minimum
and maximum electrical
value, eq. (40) is the
appropriate formula
for
determining
the SNR.
If the ADC is adjusted so
that 0 corresponds to the
minimum
electrical
value and 2B-1 corresponds to
the maximum electrical value
then:
SNR
= 6
B
+ 11
dB
(68)
Quantization
noise
For
B
≥ 8
bits, this means a SNR
≥ 59
dB. Quantization noise can
usually be
ignored
as the total SNR
of a complete
system is typically dominated by
the
smallest
SNR.
In CCD cameras this is
photon noise.
7.
Cameras
The
cameras and recording media
available for modern digital
image processing
applications
are changing at a significant
pace. To dwell too long in
this section on
one
major type of camera, such as
the CCD camera, and to ignore
developments in
areas
such as charge injection device
(CID) cameras and CMOS
cameras is to run
the
risk of obsolescence. Nevertheless, the
techniques that are used to
characterize
the
CCD camera remain "universal"
and the presentation that
follows is given in
the
context of modern CCD
technology for purposes of
illustration.
35

...Image
Processing Fundamentals
7.1
LINEARITY
It
is generally desirable that the
relationship between the
input physical signal
(e.g.
photons)
and the output signal
(e.g. voltage) be linear.
Formally this means (as
in
eq.
(20)) that if we have two
images, a
and b, and two
arbitrary complex
constants,
w1 and w2 and a
linear camera response,
then:
c
=
R {w1a
+ w2b} = w1R
{a} + w2R
{b
}
(69)
where
R{�} is the
camera response and c
is the
camera output. In practice
the
relationship
between input a
and output
c
is frequently
given by:
c
= gain
� aγ + offset
(70)
where
γ is the
gamma
of the
recording medium. For a
truly linear recording
system
we
must have γ
= 1
and offset
= 0.
Unfortunately, the offset is
almost never zero
and
thus we must compensate for
this if the intention is to
extract intensity
measurements.
Compensation techniques are
discussed in Section 10.1.
Typical
values of γ
that
may be encountered are
listed in Table 8. Modern
cameras
often
have the ability to switch
electronically between various values of
γ.
γ
Sensor
Surface
Possible
advantages
CCD
chip
Silicon
1.0
Linear
Compresses
dynamic range →
high
contrast scenes
Vidicon
Tube
Sb2S3
0.6
Compresses
dynamic range →
high
contrast scenes
Film
Silver
halide
<
1.0
Expands
dynamic range →
low
contrast scenes
Film
Silver
halide
>
1.0
Table
8: Comparison of
γ of various
sensors
7.2
SENSITIVITY
There
are two ways to describe
the sensitivity of a camera. First, we
can determine
the
minimum number of detectable
photoelectrons. This can be termed
the absolute
sensitivity.
Second, we can describe the
number of photoelectrons necessary
to
change
from one digital brightness
level to the next, that
is, to change one analog-
to-digital
unit (ADU).
This can be termed the
relative
sensitivity.
7.2.1
Absolute sensitivity
To
determine the absolute
sensitivity we need a characterization of
the camera in
terms
of its noise. If the total
noise has a σ
of,
say, 100 photoelectrons,
then to
ensure
detectability of a signal we could
then say that, at the
3σ level,
the minimum
detectable
signal (or absolute
sensitivity) would be 300
photoelectrons. If all
the
noise
sources listed in Section 6, with
the exception of photon noise,
can be reduced
36

...Image
Processing Fundamentals
to
negligible levels, this
means that an absolute
sensitivity of less than
10
photoelectrons
is achievable with modern
technology
7.2.2
Relative sensitivity
The
definition of relative sensitivity,
S, given above
when coupled to the linear
case,
eq.
(70) with γ
= 1,
leads immediately to the
result:
S
= 1
gain
= gain-1
(71)
The
measurement of the sensitivity
or gain
can be performed
in two distinct ways.
�
If, following eq. (70), the
input signal a
can be precisely
controlled by either
"shutter"
time or intensity (through
neutral density filters),
then the gain can
be
estimated
by estimating the slope of
the resulting straight-line
curve. To translate
this
into the desired units,
however, a standard source
must be used that emits
a
known
number of photons onto the
camera sensor and the quantum
efficiency (η)
of
the sensor must be known.
The quantum efficiency
refers to how many
photoelectrons
are produced--on the
average--per photon at a given
wavelength.
In
general 0 ≤
η(λ)
≤ 1.
�
If, however, the limiting
effect of the camera is only
the photon (Poisson)
noise
(see
Section 6.1), then an
easy-to-implement, alternative technique
is available to
determine
the sensitivity. Using
equations (63), (70), and
(71) and after
compensating
for the offset
(see
Section 10.1), the sensitivity measured
from an
image
c
is given
by:
E{c}
m
S=
=
2c
(72)
Var{c} sc
where
mc and sc are
defined in equations (34) and
(36).
Measured
data for five modern (1995)
CCD camera configurations
are given in
Table
9.
Camera
Pixels
Pixel
size
Temp.
S
Bits
Label
�m
x �m
K
e
/ ADU
C1
1320
x 1035
6.8
x 6.8
231
7.9
12
C2
578
x 385
22.0
x 22.0
227
9.7
16
C3
1320
x 1035
6.8
x 6.8
293
48.1
10
C4
576
x 384
23.0
x 23.0
238
90.9
12
C5
756
x 581
11.0
x 5.5
300
109.2
8
Table
9: Sensitivity
measurements. Note that a
more
sensitive
camera has a lower value of
S.
37

...Image
Processing Fundamentals
The
extraordinary sensitivity of modern
CCD cameras is clear from
these data. In a
scientific-grade
CCD camera (C1), only 8
photoelectrons (approximately 16
photons)
separate two gray levels in
the digital representation of
the image. For a
considerably
less expensive video camera
(C5), only about 110
photoelectrons
(approximately
220 photons) separate two
gray levels.
7.3
SNR
As
described in Section 6, in modern
camera systems the noise is
frequently
limited
by:
�
amplifier noise in the
case of color
cameras;
�
thermal noise which,
itself, is limited by the
chip temperature K and
the
exposure
time T,
and/or;
�
photon noise which is
limited by the photon
production rate ρ
and
the
exposure
time T.
7.3.1
Thermal noise (Dark
current)
Using
cooling techniques based
upon Peltier cooling
elements it is straightforward
to
achieve chip temperatures of
230 to 250 K. This leads to low
thermal electron
production
rates. As a measure of the thermal noise,
we can look at the number
of
seconds
necessary to produce a sufficient number
of thermal electrons to go
from
one
brightness level to the
next, an ADU, in the absence
of photoelectrons. This
last
condition--the
absence of photoelectrons--is the
reason for the name
dark
current.
Measured
data for the five
cameras described above are
given in Table 10.
Camera
Temp.
Dark
Current
Label
K
Seconds
/ ADU
C1
231
526.3
C2
227
0.2
C3
293
8.3
C4
238
2.4
C5
300
23.3
Table
10: Thermal
noise characteristics
The
video
camera (C5)
has on-chip dark current
suppression. (See Section
6.2.)
Operating
at room temperature this camera
requires more than 20
seconds to
produce
one ADU change due to
thermal noise. This means at
the conventional
video
frame and integration rates
of 25 to 30 images per second (see Table
3), the
thermal
noise is negligible.
7.3.2
Photon noise
From
eq. (64) we see that it
should be possible to increase the
SNR
by
increasing
the
integration time of our image and
thus "capturing" more
photons. The pixels
in
38

...Image
Processing Fundamentals
CCD
cameras have, however, a
finite well capacity. This
finite capacity, C,
means
that
the maximum SNR
for a
CCD camera per pixel is
given by:
SNR
= 10
log10 (C)
dB
(73)
Capacity-limited
photon noise
Theoretical
as well as measured data for
the five cameras described
above are given
in
Table 11.
Camera
C
Theor.
SNR
Meas.
SNR
Pixel
size
Well
Depth
#
e / �m 2
Label
#
e
dB
dB
�m
x �m
C1
32,000
45
45
6.8
x 6.8
692
C2
340,000
55
55
22.0
x 22.0
702
C3
32,000
45
43
6.8
x 6.8
692
C4
400,000
56
52
23.0
x 23.0
756
C5
40,000
46
43
11.0
x 5.5
661
Table
11: Photon
noise characteristics
Note
that for certain cameras,
the measured SNR
achieves
the theoretical,
maximum
indicating that the
SNR
is,
indeed, photon and well capacity
limited.
Further,
the curves of SNR
versus
T
(integration
time) are consistent with
equations
(64)
and (73). (Data not shown.)
It can also be seen that, as a consequence of
CCD
technology,
the "depth" of a CCD pixel
well is constant at about
0.7 ke / �m2.
7.4
SHADING
Virtually
all imaging systems produce shading. By
this we mean that if the
physical
input
image a(x,y)
= constant,
then the digital version of
the image will not be
constant.
The source of the shading
might be outside the camera
such as in the
scene
illumination or the result of
the camera itself where a
gain
and
offset
might
vary
from pixel to pixel. The
model for shading is given
by:
c[m, n]
=
gain[
m, n]
� a[m
, n]
+
offset[m, n]
(74)
where
a[m,n] is the
digital image that would
have been recorded if there
were no
shading
in the image, that is,
a[m,n] = constant.
Techniques for reducing
or
removing
the effects of shading are
discussed in Section 10.1.
7.5
P IXEL F
ORM
While
the pixels shown in Figure 1
appear to be square and to "cover"
the
continuous
image, it is important to know the
geometry for a given
camera/digitizer
system.
In Figure 18 we define possible
parameters associated with a camera
and
digitizer
and the effect they
have upon the
pixel.
39

...Image
Processing Fundamentals
Xo
Xa
Ya
=
photosensitive region
=
nonsensitive region
Yo
Figure
18: Pixel
form parameters
The
parameters Xo and Yo are
the spacing between the
pixel centers and
represent
the
sampling distances from equation
(52). The parameters
Xa and Ya are
the
dimensions
of that portion of the
camera's surface that is
sensitive to light. As
mentioned
in Section 2.3, different
video digitizers (frame grabbers) can
have
different
values for Xo while
they have a common value
for Yo.
7.5.1
Square pixels
As
mentioned in Section 5, square sampling
implies that Xo = Yo or alternatively
Xo
/
Yo = 1. It is not
uncommon, however, to find
frame grabbers where
Xo / Yo = 1.1
or
Xo / Yo = 4/3.
(This latter format matches
the format of commercial
television.
See
Table 3) The risk associated
with non-square pixels is
that isotropic
objects
scanned
with non-square pixels might
appear isotropic on a
camera-compatible
monitor
but analysis of the objects
(such as length-to-width ratio) will
yield non-
isotropic
results. This is illustrated in
Figure 19.
Analog
object
Digitizing
raster
Digital
image
↓
↓
↓
+
=
1:1
Sampling
+
=
4:3
Sampling
Figure
19: Effect of
non-square pixels
40
...Image
Processing Fundamentals
The
ratio Xo / Yo can be
determined for any specific
camera/digitizer system by
using
a calibration test chart
with known distances in the
horizontal and
vertical
direction.
These are straightforward to
make with modern laser
printers. The test
chart
can then be scanned and
the sampling distances
Xo and Yo determined.
7.5.2
Fill factor
In
modern CCD cameras it is possible
that a portion of the camera
surface is not
sensitive
to light and is instead used for
the CCD electronics or to
prevent
blooming.
Blooming occurs when a CCD
well is filled (see Table
11) and
additional
photoelectrons spill over
into adjacent CCD wells.
Anti-blooming
regions
between the active CCD sites
can be used to prevent this.
This means, of
course,
that a fraction of the
incoming photons are lost as
they strike the
non-
sensitive
portion of the CCD chip.
The fraction of the surface
that is sensitive to
light
is termed the fill
factor and is
given by:
Xa � Ya
fill
factor =
�
100%
(75)
Xo � Yo
The
larger the fill
factor the
more light will be captured by the
chip up to the
maximum
of 100%. This helps improve
the SNR.
As a tradeoff, however,
larger
values
of the fill factor mean more
spatial smoothing due to the
aperture effect
described
in Section 5.1.1. This is illustrated in
Figure 16.
7.6
SPECTRAL SENSITIVITY
Sensors,
such as those found in
cameras and film, are
not equally sensitive to
all
wavelengths
of light. The spectral
sensitivity for the CCD
sensor is given in
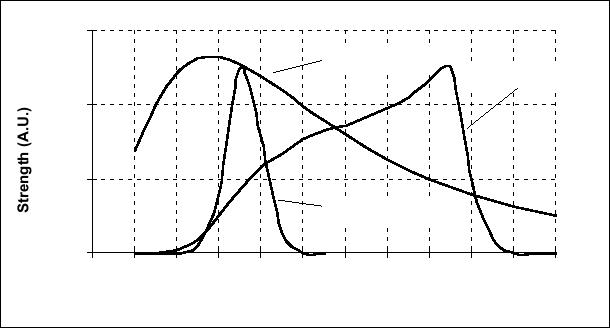
Figure
20.
41
...Image
Processing Fundamentals
1.20
Sun
Emission
Silicon
Sensitivity
0.80
0.40
Human
Sensitivity
0.00
200
300
400
500
600
700
800
900
1000 1100 1200
1300
UV
IR
Wavelength
(nm.)
Figure
20: Spectral characteristics of
silicon, the sun, and the
human visual system.
UV
= ultraviolet and IR =
infra-red.
The
high sensitivity of silicon in
the infra-red means that,
for applications where
a
CCD
(or other silicon-based)
camera is to be used as a source of
images for digital
image
processing and analysis, consideration should be
given to using an IR
blocking
filter. This filter blocks
wavelengths above 750 nm.
and thus prevents
"fogging"
of the image from the longer
wavelengths found in
sunlight.
Alternatively,
a CCD-based camera can make an excellent
sensor for the near
infrared
wavelength range of 750 nm to 1000
nm.
7.7
SHUTTER SPEEDS (INTEGRATION TIME
)
The
length of time that an image
is exposed--that photons are
collected--may be
varied
in some cameras or may vary on the
basis of video formats (see
Table 3).
For
reasons that have to do with
the parameters of photography,
this exposure time
is
usually termed shutter
speed although
integration time would be a
more
appropriate
description.
7.7.1
Video cameras
Values
of the shutter speed as low
as 500 ns are available with
commercially
available
CCD video
cameras
although the more
conventional speeds for
video are
33.37
ms (NTSC) and 40.0 ms (PAL,
SECAM). Values as high as 30 s
may also
be
achieved with certain video
cameras although this means
sacrificing a
continuous
stream of video images that
contain signal in favor of a
single integrated
image
amongst a stream of otherwise empty
images. Subsequent digitizing
hardware
must be capable of handling
this situation.
42

...Image
Processing Fundamentals
7.7.2
Scientific cameras
Again
values as low as 500 ns are
possible and, with cooling
techniques based on
Peltier-cooling
or liquid nitrogen cooling,
integration times in excess of
one hour
are
readily achieved.
7.8
READOUT RATE
The
rate at which data is read
from the sensor chip is
termed the readout
rate.
The
readout
rate for standard video
cameras depends on the parameters of the
frame
grabber
as well as the camera. For standard
video, see Section 2.3,
the readout rate
is
given by:
images
lines pixels
R=
�
�
(76)
sec
image
line
While
the appropriate unit for
describing the readout rate should be
pixels
/ second,
the
term Hz
is frequently
found in the literature and
in camera specifications; we
shall
therefore use the latter
unit. For a video camera
with square pixels (see
Section
7.5),
this means:
Format
lines
/ sec
pixels
/ line
R
(MHz.)
≈11.0
NTSC
15,750
(4/3)*525
≈13.0
PAL
/ SECAM
15,625
(4/3)*625
Table
12: Video
camera readout rates
Note
that the values in Table 12
are approximate. Exact
values for
square-pixel
systems
require exact knowledge of
the way the video
digitizer (frame
grabber)
samples
each video line.
The
readout rates used in video
cameras frequently means
that the electronic
noise
described
in Section 6.3 occurs in the
region of the noise spectrum
(eq. (65))
described
by ω
> ωmax
where the
noise power increases with
increasing frequency.
Readout
noise can thus be
significant in video
cameras.
Scientific
cameras frequently use a
slower readout rate in order to reduce
the
readout
noise. Typical values of
readout rate for scientific
cameras, such as those
described
in Tables 9, 10, and 11, are
20 kHz, 500 kHz, and 1 MHz to 8
MHz.
43
Table of Contents:
- Introduction
- Digital Image Definitions:COMMON VALUES, Types of operations, VIDEO PARAMETERS
- Tools:CONVOLUTION, FOURIER TRANSFORMS, Circularly symmetric signals
- Perception:BRIGHTNESS SENSITIVITY, Wavelength sensitivity, OPTICAL ILLUSIONS
- Image Sampling:Sampling aperture, Sampling for area measurements
- Noise:PHOTON NOISE, THERMAL NOISE, KTC NOISE, QUANTIZATION NOISE
- Cameras:LINEARITY, Absolute sensitivity, Relative sensitivity, PIXEL FORM
- Displays:REFRESH RATE, INTERLACING, RESOLUTION
- Algorithms:HISTOGRAM-BASED OPERATIONS, Equalization, Binary operations, Second Derivatives
- Techniques:SHADING CORRECTION, Estimate of shading, Unsharp masking
- Acknowledgments
- References