 |
...Image
Processing Fundamentals
4.
Perception
Many image
processing applications are intended to
produce images that are to
be
viewed by
human observers (as opposed
to, say, automated
industrial inspection.)
It
is therefore important to understand
the characteristics and limitations of
the
human
visual system--to understand
the "receiver" of the 2D
signals. At the
outset
it
is important to realize that 1)
the human visual system is
not well understood,
2)
no
objective measure exists for
judging the quality of an image
that corresponds to
human
assessment of image quality, and, 3)
the "typical" human observer
does not
exist.
Nevertheless, research in perceptual
psychology has provided
some
important
insights into the visual
system. See, for example,
Stockham [12].
4.1
BRIGHTNESS SENSITIVITY
There
are several ways to describe
the sensitivity of the human
visual system. To
begin,
let us assume that a
homogeneous region in an image
has an intensity as a
function
of wavelength (color) given by
I(λ). Further
let us assume that I(λ) = Io, a
constant.
4.1.1
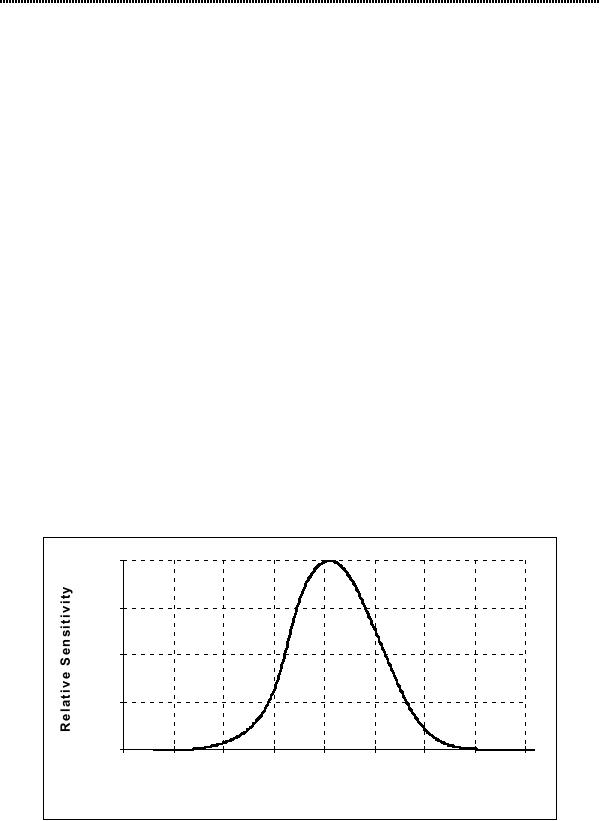
Wavelength sensitivity
The
perceived intensity as a function of
λ, the
spectral sensitivity, for
the "typical
observer"
is shown in Figure 10
[13].
1.00
0.75
0.50
0.25
0.00
350
400
450
500
550
600
650
700
750
Wavelength
(nm.)
Figure
10: Spectral
Sensitivity of the "typical"
human observer
4.1.2
Stimulus sensitivity
If
the constant intensity
(brightness) Io is allowed to
vary then, to a good
approximation,
the visual response,
R
, is proportional
to the logarithm of
the
intensity.
This is known as the
WeberFechner law:
22
...Image
Processing Fundamentals
R
= log(
Io )
(45)
The
implications of this are
easy to illustrate. Equal
perceived
steps in
brightness,
ĆR = k,
require that the physical
brightness (the stimulus)
increases exponentially.
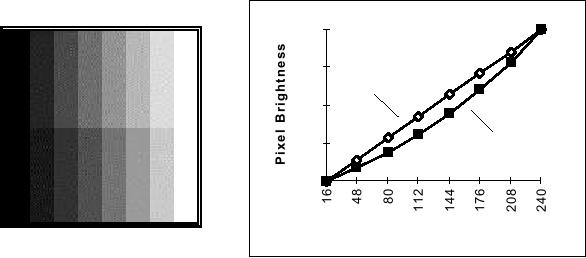
This
is illustrated in Figure 11ab.
A
horizontal line through the
top portion of Figure 11a
shows a linear increase in
objective
brightness (Figure 11b) but
a logarithmic increase in
subjective
brightness.
A horizontal line through
the bottom portion of Figure
11a shows an
exponential
increase in objective brightness (Figure
11b) but a linear increase
in
subjective
brightness.
256
192
Ć
I=k
128
Ć
I=k�I
64
0
Sampled
Postion
Figure
11a
Figure
11b
(top)
Brightness step ĆI = k
Actual
brightnesses plus interpolated
values
(bottom)
Brightness step ĆI = k�I
The
Mach band
effect is visible in
Figure 11a. Although the
physical brightness is
constant
across each vertical stripe,
the human observer perceives an
"undershoot"
and
"overshoot" in brightness at what is
physically a step edge.
Thus, just before
the
step, we see a slight
decrease in brightness compared to the
true physical value.
After
the step we see a slight
overshoot in brightness compared to the
true physical
value.
The total effect is one of
increased, local, perceived
contrast at a
step edge in
brightness.
4.2
SPATIAL F
REQUENCY SENSITIVITY
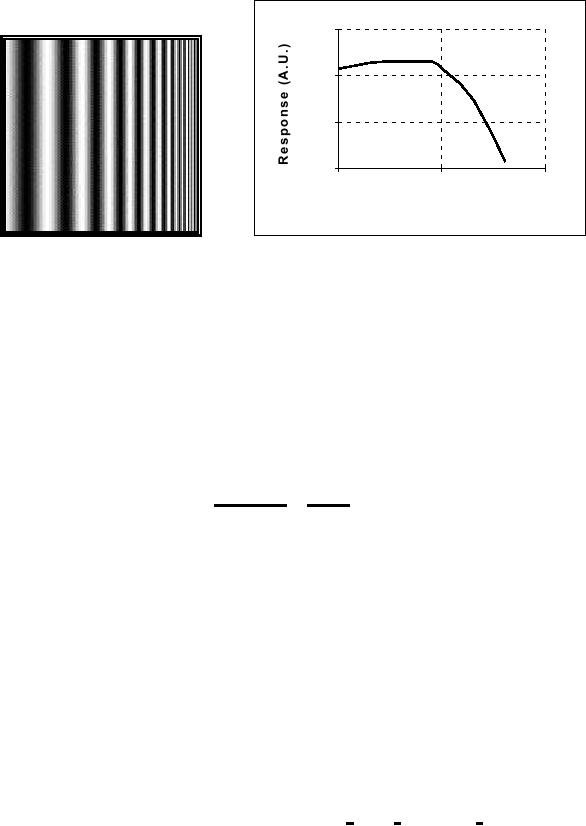
If
the constant intensity
(brightness) Io is replaced by a
sinusoidal grating with
increasing
spatial frequency (Figure
12a), it is possible to determine the
spatial
frequency
sensitivity. The result is
shown in Figure 12b [14,
15].
23
...Image
Processing Fundamentals
1000
100
10
1
1
10
100
Spatial
Frequency
(cycles/degree)
Figure
12a
Figure
12b
Sinusoidal
test grating
Spatial
frequency sensitivity
To
translate these data into
common terms, consider an
"ideal" computer
monitor
at
a viewing distance of 50 cm.
The spatial frequency that
will give maximum
response
is at 10 cycles per degree.
(See Figure 12b.) The
one degree at 50 cm
translates
to 50 tan(1�) = 0.87 cm on
the computer screen. Thus
the spatial
frequency
of maximum response fmax = 10 cycles/0.87
cm = 11.46 cycles/cm at
this
viewing distance. Translating this
into a general formula
gives:
10
572.9
f
max =
=
cycles
/ cm
(46)
d
�
tan(1�)
d
where
d
= viewing distance
measured in cm.
4.3
COLOR SENSITIVITY
Human
color perception is an exceedingly
complex topic. As such we
can only
present
a brief introduction here.
The physical perception of
color is based upon
three
color pigments in the
retina.
4.3.1
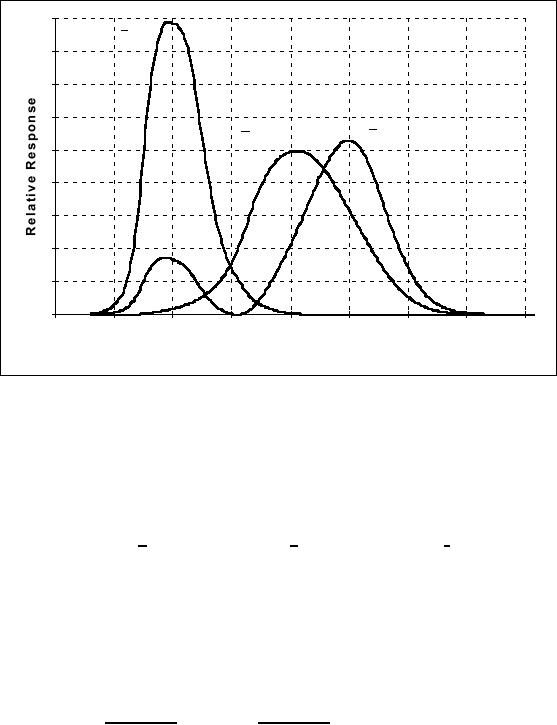
Standard observer
Based
upon psychophysical measurements,
standard curves have been adopted
by
the
CIE (Commission Internationale de
l'Eclairage) as the sensitivity
curves for the
"typical"
observer for the three
"pigments" x
(λ
),
y
(λ), and z (λ
) . These
are
shown
in Figure 13. These are not
the actual
pigment
absorption characteristics
found
in the "standard" human
retina but rather
sensitivity curves derived
from
actual
data [10].
24
...Image
Processing Fundamentals
z(λ )
x
(λ
)
y
(λ
)
350
400
450
500
550
600
650
700
750
Wavelength
(nm.)
Figure
13: Standard
observer spectral sensitivity
curves.
For
an arbitrary homogeneous region in an image
that has an intensity as a
function
of
wavelength (color) given by
I(λ), the
three responses are called
the tristimulus
values:
∞
∞
∞
X
= ∫ I(
λ )x
(λ
)dλ
Y
= ∫ I(
λ ) y
(λ
)dλ
Z
= ∫ I
(λ
)z
( λ) dλ
(47)
0
0
0
4.3.2
CIE chromaticity coordinates
The
chromaticity
coordinates which
describe the perceived color
information are
defined
as:
X
Y
x=
y=
z
= 1
- ( x
+ y)
(48)
X+Y+Z
X
+ Y +Z
The
red chromaticity coordinate is given by
x
and the green
chromaticity coordinate
by
y. The
tristimulus values are
linear in I(λ)
and thus the absolute
intensity
information
has been lost in the
calculation of the chromaticity
coordinates {x,y}.
All
color distributions, I(λ),
that appear to an observer as having
the same color
will
have the same chromaticity
coordinates.
If
we use a tunable source of pure
color (such as a dye laser),
then the intensity
can
be
modeled as I(λ)
= δ(λ
λo) with
δ(�) as
the impulse function. The
collection of
chromaticity
coordinates {x,y} that will be
generated by varying λo
gives
the CIE
chromaticity
triangle as shown in
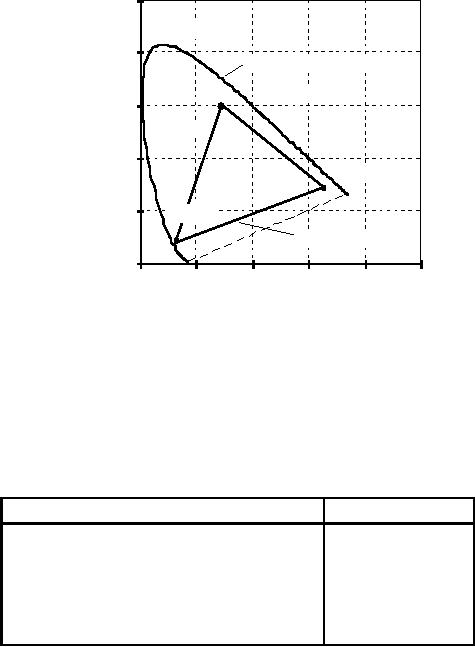
Figure 14.
25
...Image
Processing Fundamentals
1.00
520
nm.
0.80
Chromaticity
Triangle
560
nm.
0.60
500
nm.
y
0.40
640
nm.
0.20
470
nm.
Phosphor
Triangle
0.00
0.00
0.20
0.40
0.60
0.80
1.00
x
Figure
14: Chromaticity
diagram containing the
CIE
chromaticity
triangle
associated
with pure spectral colors
and the triangle
associated
with
CRT phosphors.
Pure
spectral colors are along
the boundary of the
chromaticity triangle. All
other
colors
are inside the triangle.
The chromaticity coordinates for
some standard
sources
are given in Table 6.
Source
x
y
Fluorescent
lamp @ 4800 �K
0.35
0.37
Sun
@ 6000 �K
0.32
0.33
Red
Phosphor (europium yttrium
vanadate)
0.68
0.32
Green
Phosphor (zinc cadmium
sulfide)
0.28
0.60
Blue
Phosphor (zinc
sulfide)
0.15
0.07
Table
6: Chromaticity
coordinates for standard
sources.
The
description of color on the
basis of chromaticity coordinates
not only permits
an
analysis of color but
provides a synthesis technique as
well. Using a mixture
of
two
color sources, it is possible to generate
any of the colors along
the line
connecting
their respective chromaticity
coordinates. Since we cannot have
a
negative
number of photons, this means
the mixing coefficients must
be positive.
Using
three color sources such as
the red, green, and blue
phosphors on CRT
monitors
leads to the set of colors
defined by the interior
of the
"phosphor
triangle"
shown in Figure 14.
26

...Image
Processing Fundamentals
The
formulas for converting from
the tristimulus values
(X,Y,Z) to the
well-known
CRT
colors (R
,G,B ) and
back are given
by:
R 1.9107
-0.5326
-0.2883
X
G = -0.9843
1.9984 -0.0283 �
Y
(49)
B 0.0583
-
0.1185
0.8986
Z
and
X
0.6067
0.1736 0.2001
R
Y
= 0.2988
0.5868 0.1143
� G
(50)
Z 0.0000
0.0661 1.1149
B
As
long as the position of a
desired color (X,Y,Z)
is inside the phosphor
triangle in
Figure
14, the values of R , G,
and B
as computed by eq.
(49) will be positive
and
can
therefore be used to drive a
CRT monitor.
It
is incorrect to assume that a
small displacement anywhere in
the chromaticity
diagram
(Figure 14) will produce a
proportionally small change in
the perceived
color.
An empirically-derived chromaticity space
where this property
is
approximated
is the (u',v')
space:
4x
9y
u'
=
v'
=
-2 x
+ 12
y
+ 3
-2 x
+ 12
y
+ 3
and
(51)
9u'
4v'
x=
y=
6u' -16 v'
+ 12
6u' -
16v'
+12
Small
changes almost anywhere in the
(u',v')
chromaticity space produce
equally
small
changes in the perceived
colors.
4.4
OPTICAL ILLUSIONS
The
description of the human
visual system presented above is
couched in standard
engineering
terms. This could lead one to
conclude that there is
sufficient
knowledge
of the human visual system
to permit modeling the
visual system with
standard
system analysis techniques. Two
simple examples of optical
illusions,
shown
in Figure 15, illustrate
that this system approach
would be a gross
oversimplification.
Such models should only be
used with extreme
care.
27
Table of Contents:
- Introduction
- Digital Image Definitions:COMMON VALUES, Types of operations, VIDEO PARAMETERS
- Tools:CONVOLUTION, FOURIER TRANSFORMS, Circularly symmetric signals
- Perception:BRIGHTNESS SENSITIVITY, Wavelength sensitivity, OPTICAL ILLUSIONS
- Image Sampling:Sampling aperture, Sampling for area measurements
- Noise:PHOTON NOISE, THERMAL NOISE, KTC NOISE, QUANTIZATION NOISE
- Cameras:LINEARITY, Absolute sensitivity, Relative sensitivity, PIXEL FORM
- Displays:REFRESH RATE, INTERLACING, RESOLUTION
- Algorithms:HISTOGRAM-BASED OPERATIONS, Equalization, Binary operations, Second Derivatives
- Techniques:SHADING CORRECTION, Estimate of shading, Unsharp masking
- Acknowledgments
- References