 |
Digital Image Definitions:COMMON VALUES, Types of operations, VIDEO PARAMETERS |
| << Introduction |
| Tools:CONVOLUTION, FOURIER TRANSFORMS, Circularly symmetric signals >> |
...Image
Processing Fundamentals
regionsofinterest,
ROIs,
or simply regions.
This concept reflects the
fact that
images
frequently contain collections of objects
each of which can be the
basis for a
region. In a
sophisticated image processing
system it should be possible to
apply
specific image
processing operations to selected regions.
Thus one part of an image
(region)
might be processed to suppress motion
blur while another part
might be
processed
to improve color
rendition.
The
amplitudes of a given image will
almost always be either real
numbers or
integer
numbers. The latter is
usually a result of a quantization
process that converts
a
continuous range (say,
between 0 and 100%) to a
discrete number of levels.
In
certain
image-forming processes, however,
the signal may involve
photon counting
which
implies that the amplitude
would be inherently quantized. In
other image
forming
procedures, such as magnetic resonance
imaging, the direct
physical
measurement
yields a complex number in
the form of a real magnitude
and a real
phase.
For the remainder of this
book we will consider amplitudes as reals
or
integers
unless otherwise indicated.
2.
Digital
Image Definitions
A
digital image a[m,n]
described in a 2D discrete space is
derived from an
analog
image
a(x,y) in a 2D
continuous space through a
sampling process
that is
frequently
referred to as digitization. The
mathematics of that sampling
process will
be
described in Section 5. For
now we will look at some
basic definitions
associated
with the digital image. The
effect of digitization is shown in
Figure 1.
The
2D continuous image a(x,y)
is divided into N
rows and M
columns.
The
intersection
of a row and a column is
termed a pixel.
The value assigned to
the
integer
coordinates [m,n] with
{m=0,1,2,...,M1} and
{n=0,1,2,...,N1} is
a[m,n].
In
fact, in most cases
a(x,y)--which we might
consider to be the physical
signal
that
impinges on the face of a 2D sensor--is
actually a function of many
variables
including
depth (z),
color (λ), and time
(t). Unless
otherwise stated, we will
consider
the case of 2D,
monochromatic, static images in this
chapter.
2

...Image
Processing Fundamentals
Columns
Value
= a(x,
y, z,
λ, t)
Figure
1: Digitization of a
continuous image. The pixel
at coordinates
[m=10,
n=3]
has the integer brightness
value 110.
The
image shown in Figure 1 has
been divided into N = 16 rows
and M
= 16
columns.
The value assigned to every
pixel is the average brightness in
the pixel
rounded
to the nearest integer value.
The process of representing
the amplitude of
the
2D signal at a given coordinate as an
integer value with L different
gray levels is
usually
referred to as amplitude quantization or
simply quantization.
2.1
COMMON VALUES
There
are standard values for
the various parameters encountered in
digital image
processing.
These values can be caused by video
standards, by algorithmic
requirements,
or by the desire to keep digital
circuitry simple. Table 1
gives some
commonly
encountered values.
Parameter
Symbol
Typical
values
N
Rows
256,512,525,625,1024,1035
M
Columns
256,512,768,1024,1320
L
Gray
Levels
2,64,256,1024,4096,16384
Table
1: Common
values of digital image
parameters
Quite
frequently we see cases of
M=N=2K
where
{K
= 8,9,10}.
This can be
motivated
by digital circuitry or by the
use of certain algorithms
such as the (fast)
Fourier
transform (see Section
3.3).
3
...Image
Processing Fundamentals
The
number of distinct gray
levels is usually a power of 2,
that is, L=2B
where
B
is
the
number of bits in the binary
representation of the brightness
levels. When B
>1
we
speak of a gray-level
image; when
B
=1 we speak of a
binary
image. In a
binary
image
there are just two
gray levels which can be
referred to, for example,
as
"black"
and "white" or "0" and
"1".
2.2
CHARACTERISTICS OF IMAGE
OPERATIONS
There
is a variety of ways to classify and
characterize image operations. The
reason
for
doing so is to understand what
type of results we might
expect to achieve with
a
given
type of operation or what
might be the computational
burden associated
with
a
given operation.
2.2.1
Types of operations
The
types of operations that can be
applied to digital images to
transform an input
image
a[m,n] into an
output image b[m,n]
(or another representation) can be
classified
into three categories as shown in
Table 2.
Operation
Characterization
Generic
Complexity/Pixel
�
Point
constant
the output value at a specific
coordinate is dependent
only
on the input value at that
same coordinate.
P2
�
Local
the output value at a
specific coordinate is dependent
on
the
input values in the neighborhood
of that
same
coordinate.
N2
�
Global
the output value at a
specific coordinate is dependent
on
all
the values in the input
image.
Table
2: Types of image
operations. Image size = N
� N; neighborhood
size
=
P
� P . Note
that the complexity is specified in
operations per
pixel.
This
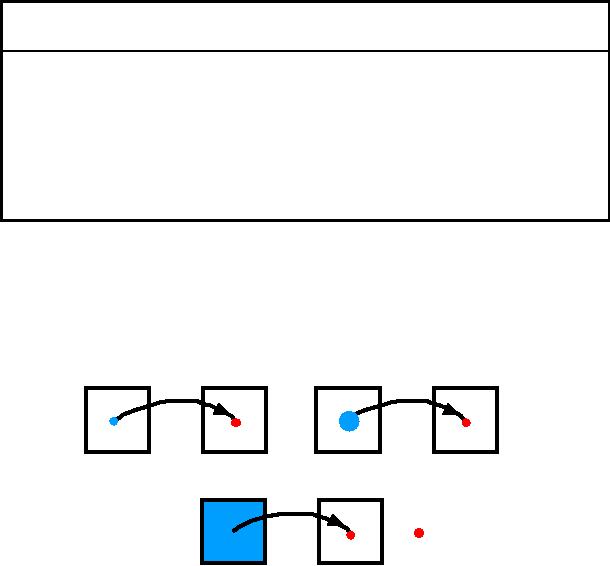
is shown graphically in Figure
2.
a
b
a
b
Point
Local
a
Global
b
=
[m=mo,
n=no]
Figure
2: Illustration of
various types of image
operations
4
...Image
Processing Fundamentals
2.2.2
Types of neighborhoods
Neighborhood
operations play a key role
in modern digital image processing. It
is
therefore
important to understand how
images can be sampled and how that
relates
to
the various neighborhoods
that can be used to process
an image.
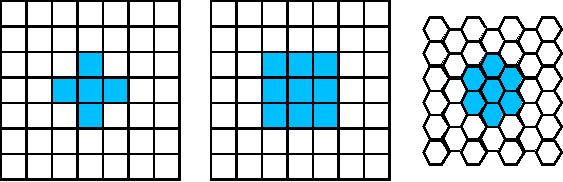
�
Rectangular sampling In most
cases, images are sampled by
laying a
rectangular
grid over an image as illustrated in
Figure 1. This results in
the type of
sampling
shown in Figure 3ab.
�
Hexagonal sampling An alternative
sampling scheme is shown in
Figure 3c and
is
termed hexagonal
sampling.
Both
sampling schemes have been studied
extensively [1] and both represent
a
possible
periodic tiling of the continuous image
space. We will restrict
our
attention,
however, to only rectangular
sampling as it remains, due to hardware
and
software
considerations, the method of
choice.
Local
operations produce an output pixel value
b[m=mo,n=no] based
upon the pixel
values
in the neighborhood
of a[m=mo,n=no]. Some of
the most common
neighborhoods
are the 4-connected neighborhood
and the 8-connected
neighborhood
in the case of rectangular
sampling and the 6-connected
neighborhood
in the case of hexagonal
sampling illustrated in Figure
3.
Figure
3a
Figure
3b
Figure
3c
Rectangular
sampling
Rectangular
sampling
Hexagonal
sampling
4-connected
8-connected
6-connected
2.3
VIDEO P
ARAMETERS
We
do not propose to describe the processing
of dynamically changing images in
this
introduction. It is appropriate--given
that many static images
are derived from
video
cameras and frame grabbers--
to mention the standards that
are associated
with
the three standard video
schemes that are currently
in worldwide use
NTSC,
PAL,
and SECAM. This information is
summarized in Table 3.
5
Table of Contents:
- Introduction
- Digital Image Definitions:COMMON VALUES, Types of operations, VIDEO PARAMETERS
- Tools:CONVOLUTION, FOURIER TRANSFORMS, Circularly symmetric signals
- Perception:BRIGHTNESS SENSITIVITY, Wavelength sensitivity, OPTICAL ILLUSIONS
- Image Sampling:Sampling aperture, Sampling for area measurements
- Noise:PHOTON NOISE, THERMAL NOISE, KTC NOISE, QUANTIZATION NOISE
- Cameras:LINEARITY, Absolute sensitivity, Relative sensitivity, PIXEL FORM
- Displays:REFRESH RATE, INTERLACING, RESOLUTION
- Algorithms:HISTOGRAM-BASED OPERATIONS, Equalization, Binary operations, Second Derivatives
- Techniques:SHADING CORRECTION, Estimate of shading, Unsharp masking
- Acknowledgments
- References