 |
Techniques:SHADING CORRECTION, Estimate of shading, Unsharp masking |
| << Algorithms:HISTOGRAM-BASED OPERATIONS, Equalization, Binary operations, Second Derivatives |
| Acknowledgments >> |

...Image
Processing Fundamentals
a)
Dilation
b)
Erosion
c)
Smoothing
d)
Gradient
e)
Laplacian
Figure
46: Examples of
gray-level morphological
filters.
10.
Techniques
The
algorithms presented in Section 9
can be used to build techniques to
solve
specific
image processing problems.
Without presuming to present
the solution to
all
processing problems, the following
examples are of general
interest and can be
used
as models for solving
related problems.
10.1
SHADING CORRECTION
The
method by which images are
produced--the interaction between objects in
real
space,
the illumination, and the
camera--frequently leads to situations
where the
image
exhibits significant shading
across the field-of-view. In
some cases the
image
might be bright in the
center and decrease in
brightness as one goes to
the
edge
of the field-of-view. In other
cases the image might be
darker on the left
side
and
lighter on the right side.
The shading might be caused
by non-uniform
illumination,
non-uniform camera sensitivity, or
even dirt and dust on
glass (lens)
surfaces.
In general this shading
effect is undesirable. Eliminating it is
frequently
necessary
for subsequent processing and especially
when image analysis or image
understanding
is the final goal.
85
...Image
Processing Fundamentals
10.1.1
Model of shading
In
general we begin with a
model for the shading
effect. The illumination
Iill(x,y)
usually
interacts in a multiplicative with
the object a(x,y)
to produce the image
b(x,y):
b(
x
, y)
=
Iill (
x, y)
· a( x,
y)
(184)
with
the object representing various
imaging modalities such
as:
r(x
, y)
reflectance
model
-OD( x
, y)
a(
x
, y)
= 10
absorption
model
(185)
c ( x,
y
)
fluorescence
model
where
at position (x,y), r(x,y)
is the reflectance,
OD
(x,y) is the
optical
density,
and
c(x,y)
is the concentration of fluorescent
material. Parenthetically, we note
that the
fluorescence
model only holds for
low concentrations. The
camera may then
contribute
gain
and offset
terms, as in
eq. (74), so that:
c[m, n]
=
gain[m, n]
· b[ m,
n
] +
offset[
m, n
]
(186)
Total
shading
=
gain[m , n]
· Iill [m, n]
· a[m
, n]
+
offset[
m, n]
In
general we assume that Iill[m,n]
is slowly varying compared to a[m,n].
10.1.2
Estimate of shading
We
distinguish between two
cases for the determination
of a[m,n] starting
from
c[m,n].
In both cases we intend to estimate
the shading terms {gain[m,n]·Iill[m,n]}
and
{offset[m,n]}.
While in the first case we
assume that we have only
the recorded
image
c[m,n] with
which to work, in the second
case we assume that we can
record
two,
additional, calibration
images.
·
A
posteriori estimate In this
case we attempt to extract
the shading estimate
from
c[m,n]. The
most common possibilities
are the following.
Lowpass
filtering We compute a
smoothed version of c[m,n]
where the
smoothing
is large compared to the size of the
objects in the image. This
smoothed
version
is intended to be an estimate of the
background of the image. We
then
subtract
the smoothed version from
c[m,n] and
then restore the desired DC
value.
In
formula:
a[m, n]
=
c[m
, n]
-
LowPass{c[m, n]}
+ constant
^
(187)
Lowpass
86
...Image
Processing Fundamentals
^
where
a[m,
n] is the
estimate of a[m,n].
Choosing the appropriate
lowpass filter
means
knowing the appropriate spatial
frequencies in the Fourier
domain where the
shading
terms dominate.
Homomorphic
filtering We note
that, if the offset[m,n]
= 0, then c[m,n]
consists
solely
of multiplicative terms. Further,
the term {gain[m,n]·Iill[m,n]}
is slowly
varying
while a[m,n]
presumably is not. We therefore take
the logarithm of c[m,n]
to
produce two terms one of
which is low frequency and
one of which is high
frequency.
We suppress the shading by
high pass filtering the
logarithm of c[m,n]
and
then take the exponent
(inverse logarithm) to restore the image.
This procedure
is
based on homomorphic
filtering as developed by
Oppenheim, Schafer and
Stockham
[34]. In formula:
i
) c[m , n]
=
gain[
m, n]
· Iill [m , n]
· a[ m,
n]
ii)
ln {c[m, n]}
= ln gain[m , n]
· Iill [
m, n
]
+ ln a[m,3
n]
rapi1 varying
2
14s4 ly
va4ng
4
42
4 3
dly
(188)
low
ryi
iii)
HighPass{ln{c[
m, n
]}} ≈ ln{a[m , n]}
iv
) a[m, n]
= exp{HighPass
{ln
{c[m, n]}}}
^
Morphological
filtering We again
compute a smoothed version of
c[m,n]
where
the
smoothing is large compared to the size
of the objects in the image
but this time
using
morphological smoothing as in eq.
(181). This smoothed version
is the
estimate
of the background of the
image. We then subtract the
smoothed version
from
c[m,n] and
then restore the desired DC
value. In formula:
a[m, n]
=
c[m
, n]
-
MorphSmooth{c[
m, n]}
+ constant
^
(189)
Choosing
the appropriate morphological
filter window means knowing
(or
estimating)
the size of the largest objects of
interest.
·
A priori estimate If it is
possible to record test
(calibration) images through
the
cameras
system, then the most
appropriate technique for
the removal of
shading
effects
is to record two images
BLACK
[m,n] and WHITE[m,n]. The BLACK
image is
generated
by covering the lens leading to
b[m,n] = 0 which in
turn leads to
BLACK
[m,n] = offset[m,n].
The WHITE
image is
generated by using a[m,n]
= 1 which
gives
WHITE[m,n] = gain[m,n]·Iill[m,n]
+ offset[m,n].
The correction then
becomes:
c[m, n]
-
BLACK[m
, n]
a[m, n]
=
constant
·
^
(190)
WHITE[m,
n] -
BLACK [m,
n]
The
constant
term is
chosen to produce the desired
dynamic range.
87
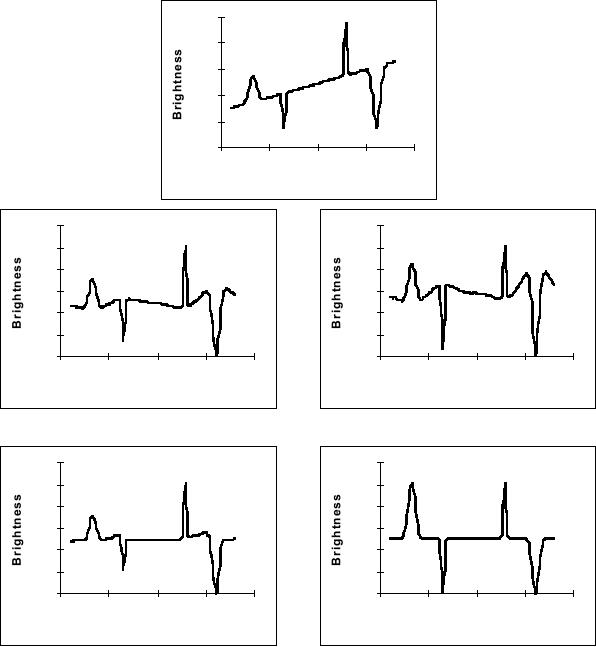
...Image
Processing Fundamentals
The
effects of these various techniques on
the data from Figure 45 are
shown in
Figure
47. The shading is a simple,
linear ramp increasing from
left to right; the
objects
consist of Gaussian peaks of varying
widths.
250
Shaded
Image
200
150
100
(a)
Original
50
0
0
50
100
150
200
Horizontal
Position
300
300
Linear
Filtering
Homomorphic
Filtering
250
250
200
200
150
150
100
100
50
50
0
0
0
50
100
150
200
0
50
100
150
200
Horizontal
Position
Horizontal
Position
(b)
Correction
with Lowpass filtering
(c)
Correction
with Logarithmic
filtering
300
300
Morphological
Filtering
"Calibration"
Filtering
250
250
200
200
150
150
100
100
50
50
0
0
0
50
100
150
200
0
50
100
150
200
Horizontal
Position
Horizontal
Position
(d)
Correction
with Max/Min
filtering
(e)
Correction
with Test Images
Figure
47: Comparison of
various shading correction
algorithms. The final
result
(e)
is identical to the original
(not shown).
In
summary, if it is possible to obtain
BLACK
and WHITE
calibration
images, then eq.
(190)
is to be preferred. If this is not
possible, then one of the other
algorithms will
be
necessary.
88
...Image
Processing Fundamentals
10.2
BASIC ENHANCEMENT AND RESTORATION
TECHNIQUES
The
process of image acquisition frequently
leads (inadvertently) to image
degradation.
Due to mechanical problems,
out-of-focus blur, motion,
inappropriate
illumination,
and noise the quality of
the digitized image can be inferior to
the
original.
The goal of enhancement
is-- starting
from a recorded image
c[m,n]--to
produce
the most visually pleasing
image â[m,n]. The
goal of restoration
is--starting
from a recorded image c[m,n]--to
produce the best possible
estimate
â[m,n]
of the original image
a[m,n]. The
goal of enhancement is beauty;
the goal of
restoration
is truth.
The
measure of success in restoration is
usually an error measure
between the
original
a[m,n] and the estimate
â[m,n]: E{â[m,n],
a[m,n]}. No
mathematical
error
function is known that corresponds to
human perceptual assessment of
error.
The mean-square
error function is commonly
used because:
1.
It is easy to compute;
2.
It is differentiable implying that a
minimum can be
sought;
3.
It corresponds to "signal energy" in the
total error, and;
4.
It has nice properties vis
à vis Parseval's
theorem, eqs. (22) and
(23).
The
mean-square error
is defined
by:
1
M
-1
N
-1
∑
∑ a[m, n]
-
a[m,
n] 2
E
{a,
a} =
^
^
(191)
MN
m = 0
n=0
In
some techniques an error measure will
not be necessary; in others it will
be
essential
for evaluation and
comparative purposes.
10.2.1
Unsharp masking
A
well-known technique from
photography to improve the
visual quality of an
image
is to enhance the edges of
the image. The technique is called
unsharp
masking.
Edge enhancement means first
isolating the edges in an
image,
amplifying
them, and then adding them
back into the image. Examination of
Figure
33
shows that the Laplacian is
a mechanism for isolating
the gray level edges.
This
leads
immediately to the
technique:
(
)
a[m, n]
=
a[m,
n] -
k
· ∇2
a[
m, n
]
^
(192)
The
term k
is the
amplifying term and k
> 0. The
effect of this technique is
shown
in
Figure 48.
89

...Image
Processing Fundamentals
The
Laplacian used to produce Figure 48 is
given by eq. (120) and
the amplification
term
k
= 1.
Original
↑
↑
Laplacian-enhanced
Figure
48: Edge
enhanced compared to
original
10.2.2
Noise suppression
The
techniques available to suppress noise
can be divided into those techniques
that
are
based on temporal information and those
that are based on spatial
information.
By
temporal information we mean
that a sequence of
images
{ap[m,n] | p=1,2,...,P } are
available that contain
exactly
the
same objects and
that
differ
only in the sense of
independent noise realizations. If
this is the case and
if
the
noise is additive, then
simple averaging of the
sequence:
1 P
a[m, n]
=
∑ a
p [ m,
n]
^
Temporal
averaging
(193)
P
p=1
will
produce a result where the
mean value of each pixel will be
unchanged. For
each
pixel, however, the standard
deviation will decrease from σ to
σ
P
.
If
temporal averaging is not possible,
then spatial averaging can be used to
decrease
the
noise. This generally
occurs, however, at a cost to image
sharpness. Four
obvious
choices for spatial averaging
are the smoothing algorithms
that have been
described
in Section 9.4 Gaussian filtering
(eq. (93)), median
filtering, Kuwahara
filtering,
and morphological smoothing (eq.
(181)).
Within
the class of linear filters,
the optimal filter for
restoration in the presence
of
noise
is given by the Wiener
filter [2].
The word "optimal" is used
here in the sense
of
minimum mean-square error (mse).
Because the square root
operation is
90

...Image
Processing Fundamentals
monotonic
increasing, the optimal
filter also minimizes the
root mean-square error
(rms).
The Wiener filter is
characterized in the Fourier
domain and for
additive
noise
that is independent of the signal it is
given by:
Saa (u,
v)
HW (u,
v) =
(194)
Saa (u,
v) +
Snn (u,
v)
where
Saa(u,v) is the
power spectral density of an
ensemble of random images
{a[m,n]} and Snn(u,v) is the
power spectral density of the
random noise. If we have
a
single image then Saa(u,v) = | A(u,v)|2. In
practice it is unlikely that
the power
spectral
density of the uncontaminated image will
be available. Because many
images
have a similar power
spectral density that can be
modeled by Table
4T.8,
that
model can be used as an
estimate of Saa(u,v).
A
comparison of the five
different techniques described above is
shown in Figure
49.
The Wiener filter was
constructed directly from eq.
(113) because the
image
spectrum
and the noise spectrum were
known. The parameters for
the other filters
were
determined choosing that
value (either σ
or
window size) that led to
the
minimum
rms.
c)
Gauss
filter (σ
=
1.0)
a)
Noisy image
(SNR=20
dB
)
b)
Wiener
filter
rms
=
25.7
rms
=
20.2
rms
=
21.1
d)
Kuwahara
filter (5 ×
5)
e)
Median
filter (3 ×
3)
f)
Morph.
smoothing (3 ×
3)
rms
=
22.4
rms
=
22.6
rms
=
26.2
Figure
49: Noise
suppression using various filtering
techniques.
91
...Image
Processing Fundamentals
The
root mean-square errors (rms)
associated with the various
filters are shown in
Figure
49. For this specific
comparison, the Wiener
filter generates a lower
error
than
any of the other procedures
that are examined here. The
two linear procedures,
Wiener
filtering and Gaussian
filtering, performed slightly better
than the three
non-
linear
alternatives.
10.2.3
Distortion suppression
The
model presented above--an image
distorted solely by noise--is
not, in general,
sophisticated
enough to describe the true
nature of distortion in a digital
image. A
more
realistic model includes not
only the noise but also a
model for the
distortion
induced
by lenses, finite apertures, possible motion of
the camera and/or an
object,
and
so forth. One frequently
used model is of an image a[m,n]
distorted by a linear,
shift-invariant
system ho[m,n] (such as a
lens) and then contaminated by noise
κ[m,n]. Various
aspects of ho[m,n] and κ[m,n] have
been discussed in earlier
sections.
The most common combination
of these is the additive
model:
c[m, n]
=
(a[m , n]
⊗
ho[ m,
n])
+ κ [m , n]
(195)
The
restoration procedure that is
based on linear filtering
coupled to a minimum
mean-square
error criterion again
produces a Wiener filter
[2]:
*
Ho (u,
v
)Saa (u,
v)
=
HW (u,
v)
2
Ho (u,
v) Saa (u,
v) +
Snn (u,
v)
(196)
*
Ho (u,
v)
=
Ho (u,
v) +
Snn (u,
v) S
(u,
v)
2
aa
Once
again Saa(u,v) is the
power spectral density of an image,
Snn(u,v) is the
power
spectral
density of the noise, and Ho(u,v) = F{ho[m,n]}. Examination of
this
formula
for some extreme cases can
be useful. For those frequencies
where
Saa(u,v) >>
Snn(u,v), where
the signal spectrum
dominates the noise
spectrum, the
Wiener
filter is given by 1/Ho(u,v), the
inverse
filter solution.
For those frequencies
where
Saa(u,v) <<
Snn(u,v), where
the noise spectrum dominates
the signal
spectrum,
the Wiener filter is
proportional to Ho*(u,v), the
matched
filter solution.
For
those frequencies where Ho(u,v) = 0, the
Wiener filter HW (u,v) = 0
preventing
overflow.
The
Wiener filter is a solution to
the restoration problem
based upon the
hypothesized
use of a linear filter and
the minimum mean-square (or
rms)
error
criterion.
In the example below the
image a[m,n]
was distorted by a bandpass
filter
92

...Image
Processing Fundamentals
and
then white noise was
added to achieve an SNR
= 30 dB . The
results are shown
in
Figure 50.
c)
Median
filter (3 ×
3)
a)
Distorted,
noisy image
b)
Wiener
filter
rms
=
108.4
rms
=
40.9
Figure
50: Noise
and
distortion
suppression using the Wiener
filter, eq.
(196)
and the median
filter.
The
rms
after
Wiener filtering but before
contrast stretching was 108.4;
after
contrast
stretching with eq. (77)
the final result as shown in
Figure 50b has a
mean-
square
error of 27.8. Using a 3 × 3
median
filter as shown in
Figure 50c leads to a
rms
error of
40.9 before contrast
stretching and 35.1 after
contrast stretching.
Although
the Wiener filter gives
the minimum rms
error
over the set of all
linear
filters,
the non-linear
median
filter gives a lower
rms
error.
The operation contrast
stretching
is itself a
non-linear operation. The "visual
quality" of the
median
filtering
result is comparable to the
Wiener filtering result.
This is due in part
to
periodic
artifacts introduced by the
linear filter which are
visible in Figure 50b.
10.3
SEGMENTATION
In
the analysis of the objects
in images it is essential that we can
distinguish
between
the objects of interest and
"the rest." This latter
group is also referred to as
the
background. The techniques
that are used to find the
objects of interest are
usually
referred to as segmentation
techniques segmenting
the foreground from
background.
In this section we will
two of the most
common
techniques--thresholding
and
edge
finding-- and we will
present techniques
for
improving
the quality of the segmentation
result. It is important to understand
that:
·
there is no
universally applicable segmentation technique
that will work for
all
images,
and,
·
no
segmentation technique is perfect.
10.3.1
Thresholding
This
technique is based upon a
simple concept. A parameter θ
called
the brightness
threshold
is chosen
and applied to the image
a[m,n] as
follows:
93
...Image
Processing Fundamentals
If
a[m , n]
≥
θ
a[m, n]
=
object
= 1
(197)
a[m , n]
=
background
=0
Else
This
version of the algorithm
assumes that we are
interested in light objects on
a
dark
background. For dark objects on a
light background we would
use:
If
a[m , n]
<
θ
a[m, n]
=
object
= 1
(198)
a[m , n]
=
background
=0
Else
The
output is the label "object"
or "background" which, due to
its dichotomous
nature,
can be represented as a Boolean
variable "1" or "0". In principle,
the test
condition
could be based upon some
other property than simple
brightness (for
example,
If
(Redness
{a[m,n]}
≥
θred
), but
the concept is clear.
The
central question in thresholding
then becomes: How do we
choose the
threshold
θ? While
there is no universal procedure
for threshold selection that
is
guaranteed
to work on all images, there
are a variety of
alternatives.
·
Fixed threshold One
alternative is to use a threshold
that is chosen
independently
of the image data. If it is known
that one is dealing with
very high-
contrast
images where the objects
are very dark and the
background is
homogeneous
(Section 10.1) and very
light, then a constant
threshold of 128 on a
scale
of 0 to 255 might be sufficiently
accurate. By accuracy we mean that
the
number
of falsely-classified pixels should be
kept to a minimum.
·
Histogram-derived thresholds In most
cases the threshold is
chosen from the
brightness
histogram of the region or image
that we wish to segment. (See
Sections
3.5.2
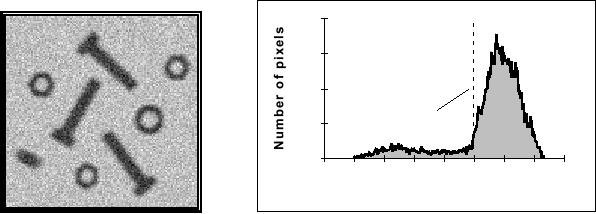
and 9.1.) An image and
its associated brightness histogram
are shown in
Figure
51.
A
variety of techniques have
been devised to automatically choose a
threshold
starting
from the gray-value
histogram, {h[b] | b = 0, 1, ... ,
2B1}. Some of
the
most
common ones are presented
below. Many of these
algorithms can benefit
from
a smoothing of the raw
histogram data to remove
small fluctuations but
the
smoothing
algorithm must not shift
the peak positions. This
translates into a
zero-
phase
smoothing algorithm given
below where typical values
for W
are 3 or
5:
1
(W -1)
/ 2
∑
hraw [b
- w]
hsmooth[
b] =
W
odd
(199)
W
w =- (W -1)
/ 2
94
...Image
Processing Fundamentals
400
h[b]
Object
Background
300
200
Threshold
100
0
0
32
64
96
128 160 192 224
256
b
Brightness
(a)
Image to be
thresholded
(b)
Brightness
histogram of the image
Figure
51: Pixels
below the threshold
(a[m,n] < θ) will be labeled
as object pixels;
those
above the threshold will be labeled as
background pixels.
·
Isodata algorithm This
iterative technique for
choosing a threshold was
developed
by Ridler and Calvard [35].
The histogram is initially
segmented into
two
parts using a starting
threshold value such as θ0
= 2 B1, half the
maximum
dynamic
range. The sample mean
(mf,0 )
of the gray values
associated with the
foreground
pixels and the sample
mean (mb,0)
of the gray values associated
with
the
background pixels are
computed. A new threshold
value θ1
is now
computed as
the
average of these two sample
means. The process is repeated, based
upon the
new
threshold, until the
threshold value does not
change any more. In
formula:
(
)
θ
k
= m f , k
-1
+
mb ,k
-1
/ 2
until
θk
= θ k
-1
(200)
·
Background-symmetry algorithm This
technique assumes a distinct
and
dominant
peak for the background that
is symmetric about its
maximum. The
technique
can benefit from smoothing
as described in eq. (199).
The maximum
peak
(maxp)
is found by searching for
the maximum value in the
histogram. The
algorithm
then searches on the
non-object pixel
side of that
maximum to find a p%
point
as in eq. (39).
In
Figure 51b, where the object
pixels are located to the
left
of the
background peak
at
brightness 183, this means
searching to the right of
that peak to locate, as an
example,
the 95% value. At this
brightness value, 5% of the
pixels lie to the right
(are
above) that value. This
occurs at brightness 216 in Figure
51b. Because of the
assumed
symmetry, we use as a threshold a
displacement to the left
of
the
maximum
that is equal to the
displacement to the right
where the p%
is found. For
Figure
51b this means a threshold
value given by 183
(216 183) = 150.
In
formula:
θ
= maxp
- ( p%
-
maxp)
(201)
95
...Image
Processing Fundamentals
This
technique can be adapted
easily to the case where we
have light objects on
a
dark,
dominant background. Further, it
can be used if the object peak
dominates
and
we have reason to assume that
the brightness distribution
around the object
peak
is symmetric. An additional variation on
this symmetry theme is to
use an
estimate
of the sample standard deviation
(s
in eq.
(37)) based on one side of
the
dominant
peak and then use a
threshold based on θ
=
maxp
±
1.96s
(at
the 5%
level)
or θ
=
maxp
±
2.57s
(at
the 1% level). The choice of
"+" or "" depends on
which
direction from maxp
is being
defined as the object/background
threshold.
Should
the distributions be approximately
Gaussian around maxp,
then the values
1.96
and 2.57 will, in fact, correspond to
the 5% and 1 % level.
·
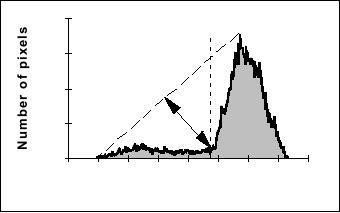
Triangle algorithm This
technique due to Zack [36]
is illustrated in Figure
52.
A
line is constructed between
the maximum of the histogram
at brightness bmax
and
the lowest value bmin =
(p=0)% in
the image. The distance
d
between
the line
and
the histogram h[b] is computed
for all values of b from
b
= b
min to
b
= b
max.
The
brightness value bo where
the distance between h[bo] and the
line is maximal is
the
threshold value, that is, θ =
bo. This
technique is particularly effective
when the
object
pixels produce a weak peak in
the histogram.
400
h[b]
Threshold
= bo
300
200
d
100
0
0
32
64
96
128 160 192 224
256
b
Brightness
Figure
52: The
triangle algorithm is based on
finding the value of
b
that
gives
the maximum distance d.
The
three procedures described above give
the values θ
= 139
for the Isodata
algorithm,
θ = 150
for the background symmetry
algorithm at the 5% level,
and θ
=
152 for the triangle
algorithm for the image in
Figure 51a.
Thresholding
does not have to be applied
to entire images but can be
used on a
region
by region basis. Chow and
Kaneko [37] developed a
variation in which
the
M
× N image is divided
into non-overlapping regions. In
each region a threshold
is
calculated
and the resulting threshold
values are put together
(interpolated) to form a
thresholding
surface for the entire
image. The regions should be
of "reasonable"
size
so that there are a
sufficient number of pixels in
each region to make an
estimate
of the histogram and the
threshold. The utility of
this procedure--like so
many
others--depends on the application at
hand.
96
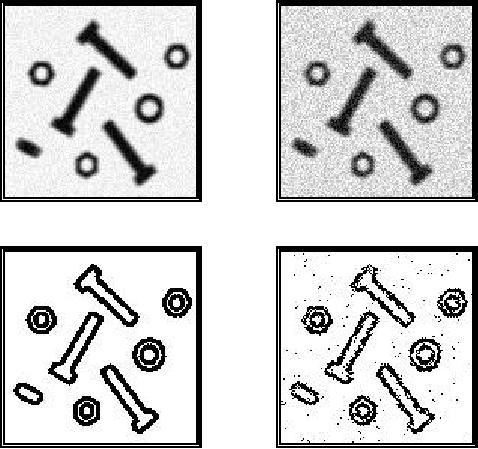
...Image
Processing Fundamentals
10.3.2
Edge finding
Thresholding
produces a segmentation that
yields all the pixels
that, in principle,
belong
to the object or objects of
interest in an image. An alternative to
this is to
find
those pixels that belong to
the borders of the objects.
Techniques that are
directed
to this goal are termed
edge
finding techniques. From
our discussion in
Section
9.6 on mathematical morphology,
specifically eqs. (79),
(163), and (170),
we
see that there is an intimate
relationship between edges and
regions.
·
Gradient-based procedure The
central challenge to edge
finding techniques is to
find
procedures that produce
closed
contours
around the objects of
interest. For
objects
of particularly high SNR,
this can be achieved by
calculating the
gradient
and
then using a suitable
threshold. This is illustrated in
Figure 53.
↓
↓
(a)
SNR
= 30 dB
(b)
SNR
= 20 dB
Figure
53: Edge
finding based on the Sobel
gradient, eq. (110),
combined
with the Isodata thresholding
algorithm eq. (92).
While
the technique works well
for the 30 dB image in Figure
53a, it fails to
provide
an accurate determination of those pixels
associated with the object
edges
for
the 20 dB image in Figure 53b. A
variety of smoothing techniques as
described
in
Section 9.4 and in eq. (181)
can be used to reduce the
noise effects before
the
gradient
operator is applied.
97
...Image
Processing Fundamentals
·
Zero-crossing based procedure
A more
modern view to handling the
problem
of
edges in noisy images is to
use the zero crossings generated in
the Laplacian of
an
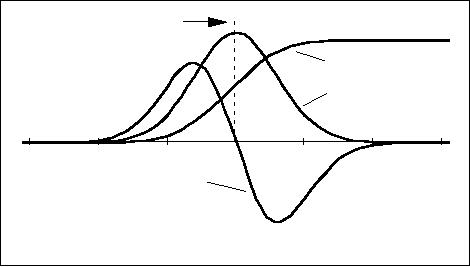
image (Section 9.5.2). The
rationale starts from the
model of an ideal edge,
a
step
function, that has been
blurred by an OTF
such as
Table 4 T.3 (out-of-focus),
T.5
(diffraction-limited), or T.6 (general
model) to produce the result
shown in
Figure
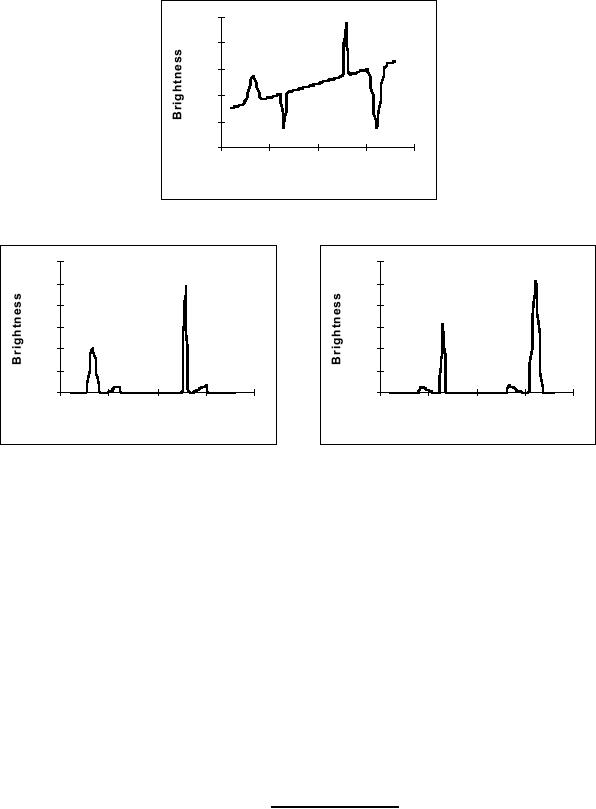
54.
Ideal
Edge Position
Blurred
Edge
Gradient
35
40
45
50
55
60
65
Laplacian
Position
Figure
54: Edge
finding based on the zero
crossing as determined by
the
second derivative, the
Laplacian. The curves are
not to scale.
The
edge location is, according
to the model, at that place
in the image where
the
Laplacian
changes sign, the zero
crossing. As the Laplacian
operation involves a
second
derivative, this means a
potential enhancement of noise in the
image at high
spatial
frequencies; see eq. (114).
To prevent enhanced noise from dominating
the
search
for zero crossings, a smoothing is
necessary.
The
appropriate smoothing filter,
from among the many
possibilities described in
Section
9.4, should according to
Canny [38] have the
following properties:
·
In the frequency domain,
(u,v)
or (Ω,Ψ),
the filter should be as
narrow as
possible
to provide suppression of high frequency
noise, and;
·
In the spatial domain,
(x,y)
or [m,n],
the filter should be as
narrow as
possible
to provide good localization of the
edge. A too wide filter
generates
uncertainty
as to precisely where, within
the filter width, the
edge is located.
The
smoothing filter that
simultaneously satisfies both these
properties--minimum
bandwidth
and minimum spatial width--is
the Gaussian filter described in
Section
9.4.
This means that the image
should be smoothed with a Gaussian of
an
appropriate
σ followed by
application of the Laplacian. In
formula:
98
...Image
Processing Fundamentals
{
}
ZeroCrossing{a( x,
y)} =
(x
, y)
| ∇
2{g2 D( x
, y)
⊗
a( x,
y)}
= 0
(202)
where
g2D(x,y) is defined in
eq. (93). The derivative
operation is linear and
shift-
invariant
as defined in eqs. (85) and
(86). This means that
the order of the
operators
can
be exchanged (eq. (4)) or
combined into one single
filter (eq. (5)). This
second
approach
leads to the Marr-Hildreth
formulation of the
"Laplacian-of-Gaussians"
(LoG)
filter [39]:
ZeroCrossing{a(
x, y)}
= {(
x, y)
| LoG(
x
, y)
⊗
a( x,
y) =
0}
(203)
where
x2 +
y2
2
LoG(
x, y
) =
g2 D( x
, y)
- 2
g2 D
(x
, y)
(204)
σ4
σ
Given
the circular symmetry this
can also be written
as:
r
2 -
2σ 2
- (r
2 / 2σ
2
)
LoG(
r) =
6
e
(205)
2šσ
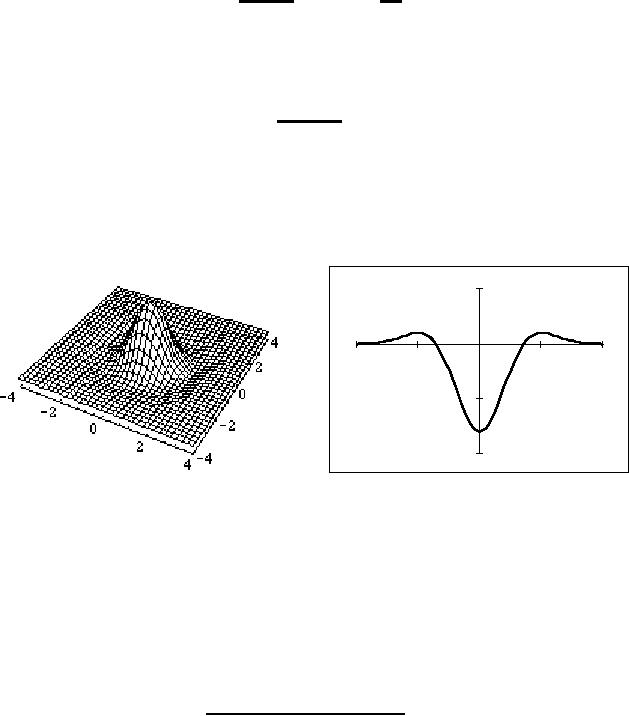
This
two-dimensional convolution kernel,
which is sometimes referred to as
a
"Mexican
hat filter", is illustrated in
Figure 55.
0.2
LoG(r)
0
-4
-2
0
2
r 4
-0.2
σ
=
1.0
-0.4
(a)
LoG(x,y)
(b)
LoG(r)
Figure
55: LoG
filter
with σ
=
1.0.
·PLUS-based
procedure Among
the zero crossing procedures
for edge detection,
perhaps
the most accurate is the
PLUS
filter as
developed by Verbeek and
Van
Vliet
[40]. The filter is defined,
using eqs. (121) and
(122), as:
PLUS(
a) =
SDGD(
a) +
Laplace
(a)
Axx Ax
+
2
Axy Ax
Ay + Ayy A2
2
(
)
(206)
y
=
+ Axx + Ayy
Ax + Ay
2
2
99
...Image
Processing Fundamentals
Neither
the derivation of the
PLUS's
properties nor an evaluation of its
accuracy are
within
the scope of this section.
Suffice it to say that, for
positively curved edges
in
gray
value images, the Laplacian-based
zero crossing procedure
overestimates the
position
of the edge and the
SDGD-based
procedure underestimates
the
position.
This
is true in both two-dimensional and
three-dimensional images with an
error on
the
order of (σ/R
)2 where R
is the
radius of curvature of the
edge. The PLUS
operator
has an error on the order of
(σ/R
)4 if the image is sampled
at, at least, 3×
the
usual Nyquist sampling
frequency as in eq. (56) or
if we choose σ
≥ 2.7
and
sample
at the usual Nyquist
frequency.
All
of the methods based on zero
crossings in the Laplacian must be able
to
distinguish
between zero crossings
and
zero values.
While the former
represent
edge
positions, the latter can be
generated by regions that are no
more complex than
bilinear
surfaces, that is, a(x,y)
= a0 + a1·x
+ a2·y
+ a3·x·y. To distinguish
between
these
two situations, we first
find the zero crossing
positions and label them as
"1"
and
all other pixels as "0". We
then multiply the resulting
image by a measure of
the
edge
strength at each pixel.
There are various measures
for the edge
strength
that
are all based on the
gradient as described in Section 9.5.1
and eq. (182).
This
last
possibility, use of a morphological
gradient as an edge strength measure,
was
first
described by Lee, Haralick, and Shapiro
[41] and is particularly
effective. After
multiplication
the image is then thresholded
(as above) to produce the
final result.
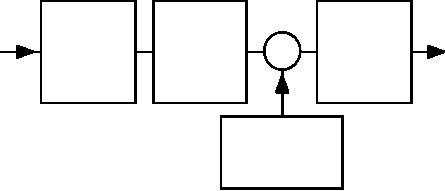
The
procedure is thus as follows
[42]:
Zero
Crossing
×
a[m,n]
edges[m,n]
Filter
Zero
Crossing
Thresholding
·
LoG
Detector
·
PLUS
·
other
Edge
Strength Filter
(Gradient)
Figure
56: General
strategy for edges based on
zero crossings.
The
results of these two edge
finding techniques based on
zero crossings, LoG
filtering
and PLUS
filtering,
are shown in Figure 57 for
images with a 20 dB SNR.
100

...Image
Processing Fundamentals
a)
Image
SNR
= 20 dB ↑↓
b)
LoG
filter
↑↓
c)
PLUS
filter
↑↓
Figure
57: Edge
finding using zero crossing
algorithms LoG
and PLUS.
In
both
algorithms σ
=
1.5.
Edge
finding techniques provide, as
the name suggests, an image
that contains a
collection
of edge pixels. Should the
edge pixels correspond to
objects, as opposed
to
say simple lines in the
image, then a region-filling
technique such as eq.
(170)
may
be required to provide the
complete objects.
10.3.3
Binary mathematical morphology
The
various algorithms that we
have described for
mathematical morphology in
Section
9.6 can be put together to
form powerful techniques for
the processing of
binary
images and gray level
images. As binary images
frequently result
from
segmentation
processes on gray level images,
the morphological processing of
the
binary
result permits the
improvement of the segmentation
result.
·
Salt-or-pepper filtering Segmentation
procedures frequently result in
isolated
"1"
pixels in a "0" neighborhood (salt) or
isolated "0" pixels in a "1"
neighborhood
(pepper). The appropriate neighborhood
definition must be chosen as
in
Figure 3. Using the lookup
table formulation for
Boolean operations in a 3 ×
3
neighborhood
that was described in association
with Figure 43, salt
filtering and
pepper
filtering are
straightforward to implement. We weight
the different
positions
in
the 3 ×
3
neighborhood as follows:
101
...Image
Processing Fundamentals
w4 =
16
w2 =
4
w3 =
8
Weights
= w5 =
32
w0 =
1
w1 =
2
(207)
w6 =
64
w7 =
128
w8 =
256
For
a 3 ×
3
window in a[m,n]
with values "0" or "1" we
then compute:
sum
= w0 a[m, n]
+
w1 a[
m
+ 1,
n] +
w2 a[m + 1,
n
- 1]
+
w3 a[
m, n
- 1]
+
w4a[m - 1,
n
- 1]
+
w5a[m - 1,
n
] +
(208)
w6a[m - 1,
n
+ 1]
+
w7a[m , n
+ 1]
+
w8 a[m + 1,
n
- 1]
The
result, sum
, is a number
bounded by 0 ≤
sum
≤ 511.
·
Salt Filter The
4-connected and 8-connected versions of
this filter are the
same
and
are given by the following
procedure:
Compute
sum
i)
(209)
If
( (sum
== 1)
c[m,n]
= 0
ii)
c[m,n]
= a[m,n]
Else
·
Pepper Filter The
4-connected and 8-connected
versions of this filter are
the
following
procedures:
4-connected
8-connected
i)
Compute sum
i)
Compute sum
(210)
ii)
If
( (sum
==
170)
ii)
If
( (sum
==
510)
c[m,n]
= 1
c[m,n]
= 1
Else
Else
c[m,n]
= a[m,n]
c[m,n]
= a[m,n]
·
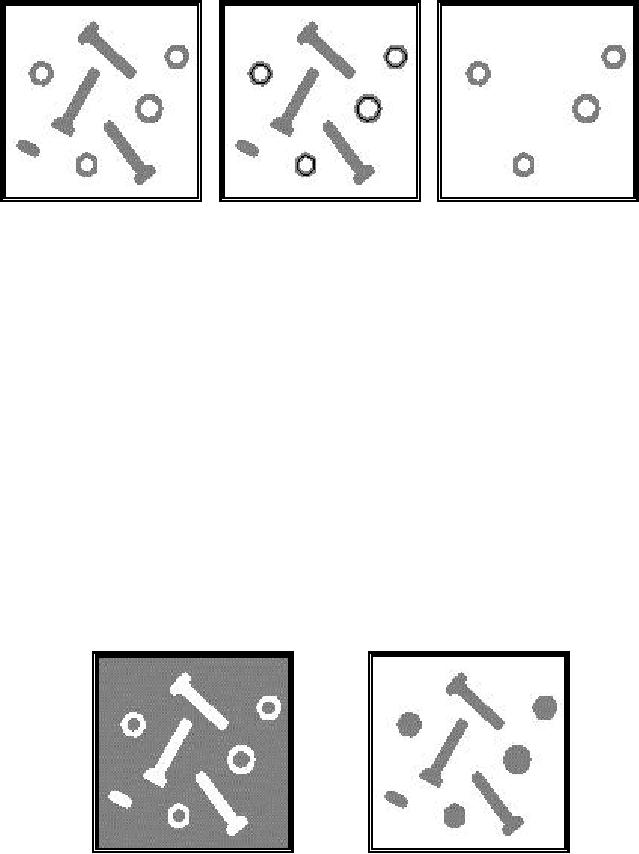
Isolate objects with holes
To find
objects with holes we can
use the following
procedure
which is illustrated in Figure
58.
Segment
image to produce
binary mask representation
i)
(211)
Compute
skeleton
without end
pixels eq.
(169)
ii)
Use
salt
filter to
remove single skeleton
pixels
iii)
Propagate
remaining
skeleton pixels into
original binary mask
eq. (170)
iv)
102
...Image
Processing Fundamentals
a)
Binary
image
b)
Skeleton after
salt filter
c)
Objects
with holes
Figure
58: Isolation
of objects with holes using
morphological operations.
The
binary objects are shown in
gray and the skeletons,
after application of the
salt
filter,
are shown as a black overlay
on the binary objects. Note
that this procedure
uses
no parameters other then the
fundamental choice of connectivity; it is
free
from
"magic numbers." In the
example shown in Figure 58,
the 8-connected
definition
was used as well as the
structuring element B =
N8.
·
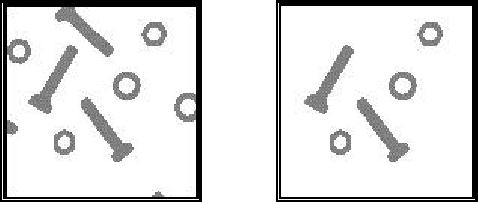
Filling holes in objects To fill
holes in objects we use the
following procedure
which
is illustrated in Figure
59.
Segment
image to produce
binary representation of objects
i)
(212)
Compute
complement
of binary image as
a mask
image
ii)
Generate
a seed
image as the border of
the image
iii)
Propagate
the
seed
into
the mask
eq.
(97)
iv)
Complement
result of
propagation to produce final
result
v)
a)
Mask and
Seed images
b)
Objects
with holes filled
Figure
59: Filling
holes in objects.
The
mask
image is illustrated in
gray
in Figure
59a and the seed
image is shown
in
black
in that
same illustration. When the
object pixels are specified
with a
connectivity
of C
= 8, then
the propagation into the mask
(background) image
103
...Image
Processing Fundamentals
should
be performed with a connectivity of
C
= 4, that
is, dilations with
the
structuring
element B
=
N4.
This procedure is also free of
"magic numbers."
·
Removing border-touching objects
Objects that are connected
to the image
border
are not suitable for
analysis. To eliminate them we can
use a series of
morphological
operations that are illustrated in
Figure 60.
Segment
image to produce
binary mask
image of
objects
i)
(213)
Generate
a seed
image as the border of
the image
ii)
Propagate
the
seed
into
the mask
eq.
(97)
iv)
Compute
XOR
of the propagation
result and the mask
image as final
result
v)
a)
Mask and
Seed images
b)
Remaining
objects
Figure
60: Removing
objects touching borders.
The
mask
image is illustrated in
gray
in Figure
60a and the seed
image is shown
in
black
in that
same illustration. If the
structuring element used in
the propagation is
B
=
N4,
then objects are removed
that are 4-connected with
the image boundary. If
B
=
N8 is
used then objects that 8-connected
with the boundary are
removed.
·
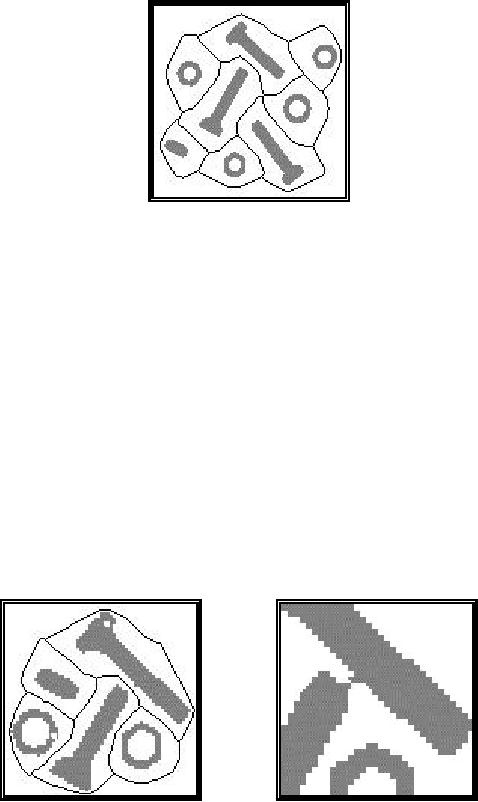
Exo-skeleton The
exo-skeleton
of a set of
objects is the skeleton of
the
background
that contains the objects.
The exo-skeleton produces a partition of
the
image
into regions each of which
contains one object. The
actual skeletonization
(eq.
(169)) is performed without
the preservation of end pixels and
with the border
set
to "0." The procedure is described
below and the result is
illustrated in Figure
61.
i)
Segment
image to produce
binary image
(214)
ii)
Compute complement
of binary
image
iii)
Compute skeleton
using
eq. (169)i+ii
with
border set to "0"
104
...Image
Processing Fundamentals
Figure
61: Exo-skeleton.
·
Touching objects Segmentation
procedures frequently have difficulty
separating
slightly
touching, yet distinct,
objects. The following
procedure provides a
mechanism
to separate these objects and
makes minimal use of "magic
numbers."
The
exo-skeleton produces a partition of
the image into regions each
of which
contains
one object. The actual skeletonization is
performed without the
preservation
of end pixels and with the
border set to "0." The
procedure is
illustrated
in Figure 62.
Segment
image to produce
binary image
i)
(215)
Compute
a "small number" of erosions
with
B
=
N4
ii)
Compute
exo-skeleton
of eroded
result
iii)
Complement
exo-skeleton
result
iv)
Compute
AND
of original
binary image and the
complemented exo-skeleton
v)
a)
Eroded and
exo-skeleton images
b)
Objects
separated (detail)
Figure
62: Separation
of touching objects.
The
eroded
binary image is illustrated in
gray
in Figure
62a and the exo-skeleton
image
is shown in
black
in that
same illustration. An enlarged
section of the final
result
is shown in Figure 62b and
the separation is easily
seen. This procedure
involves
choosing a small, minimum
number of erosions but the
number is not
critical
as long as it initiates a coarse
separation of the desired objects.
The actual
separation
is performed by the exo-skeleton
which, itself, is free of
"magic
105
...Image
Processing Fundamentals
numbers."
If the exo-skeleton is 8-connected
than the background
separating the
objects
will be 8-connected. The objects,
themselves, will be disconnected
according
to the 4-connected criterion. (See
Section 9.6 and Figure
36.)
10.3.4
Gray-value mathematical
morphology
As
we have seen in Section
10.1.2, gray-value morphological
processing
techniques
can be used for practical
problems such as shading
correction. In this
section
several other techniques will be
presented.
·
Top-hat transform The
isolation of gray-value objects
that are convex can
be
accomplished
with the top-hat
transform as developed by
Meyer [43, 44].
Depending
upon whether we are dealing
with light objects on a dark
background or
dark
objects on a light background, the
transform is defined
as:
o
TopHat(
A,
B) =
A
- (
A
B) =
A
- max
min(
A)
(216)
Light
objects
B B
TopHat(
A,
B) =
(
A
·
B) -
A
= min
max(
A) -
A
(217)
Dark
objects
B B
where
the structuring element
B
is chosen to be
bigger than the objects in
question
and,
if possible, to have a convex shape.
Because of the properties given in
eqs.
(155)
and (158), TopHat(A,B) ≥
0. An
example of this technique is
shown in
Figure
63.
The
original image including shading is
processed by a 15 ×
1
structuring element
as
described in eqs. (216) and
(217) to produce the desired
result. Note that
the
transform
for dark objects has been
defined in such a way as to
yield "positive"
objects
as opposed to "negative" objects.
Other definitions are, of course,
possible.
·
Thresholding A simple
estimate of a locally-varying threshold
surface can be
derived
from morphological processing as
follows:
1
θ
[m,
n] =
( max(A) +
min(A))
(218)
Threshold
surface
2
Once
again, we suppress the
notation for the structuring
element B
under
the max
and
min
operations to keep
the notation simple. Its
use, however, is
understood.
106
...Image
Processing Fundamentals
250
Shaded
Image
200
150
100
(a)
Original
50
0
0
50
100
150
200
Horizontal
Position
↓
↓
120
120
Top-Hat
Transform
Top-Hat
Transform
Light
objects
Dark
objects
100
100
80
80
60
60
40
40
20
20
0
0
0
50
100
150
200
0
50
100
150
200
Horizontal
Position
Horizontal
Position
(b)
Light
object transform
(c)
Dark
object transform
Figure
63: Top-hat
transforms.
·
Local contrast stretching
Using
morphological operations we can
implement a
technique
for local
contrast stretching. That
is, the amount of stretching
that will be
applied
in a neighborhood will be controlled by
the original contrast in
that
neighborhood.
The morphological gradient
defined in eq. (182) may
also be seen as
related
to a measure of the local contrast in
the window defined by the
structuring
element
B:
LocalContrast
(
A,
B) =
max(
A) -
min(
A)
(219)
The
procedure for local contrast
stretching is given
by:
A
- min(
A)
c[m, n]
=
scale
·
(220)
max(
A) -
min(
A)
The
max
and min operations are
taken over the structuring
element B. The
effect of
this
procedure is illustrated in Figure
64. It is clear that this
local
operation is
an
extended
version of the point
operation
for contrast stretching
presented in eq.
(77).
107
Table of Contents:
- Introduction
- Digital Image Definitions:COMMON VALUES, Types of operations, VIDEO PARAMETERS
- Tools:CONVOLUTION, FOURIER TRANSFORMS, Circularly symmetric signals
- Perception:BRIGHTNESS SENSITIVITY, Wavelength sensitivity, OPTICAL ILLUSIONS
- Image Sampling:Sampling aperture, Sampling for area measurements
- Noise:PHOTON NOISE, THERMAL NOISE, KTC NOISE, QUANTIZATION NOISE
- Cameras:LINEARITY, Absolute sensitivity, Relative sensitivity, PIXEL FORM
- Displays:REFRESH RATE, INTERLACING, RESOLUTION
- Algorithms:HISTOGRAM-BASED OPERATIONS, Equalization, Binary operations, Second Derivatives
- Techniques:SHADING CORRECTION, Estimate of shading, Unsharp masking
- Acknowledgments
- References