ALGORITHMS

<< Interactivity to Forms, JavaScript, server-side scripts

ALGORITHMS: Pseudo code, Flowcharts >>

Introduction to Computing CS101

LESSON 16

ALGORITHMS

Focus of the last Lesson was on Word Processing

First among the four lectures that we plan to have on productivity software, a sub-category of

application software

That first Lesson was on WP

We learnt about what we mean by WP and also desktop publishing

We also discussed the usage of various functions provided by common WP's

The Objective of Today's Lecture

To become familiar with the concept of algorithms:

What they are?

What is their use?

What do they consist of?

What are the techniques used for representing them?

Solving Problems (1)

When faced with a problem:

We first clearly define the problem

Think of possible solutions

Select the one that we think is the best under the prevailing circumstances

And then apply that solution

If the solution woks as desired, fine; else we go back to step 2

Solving Problems (2)

It is quite common to first solve a problem for a particular case

Then for another

And, possibly another

And watch for patterns and trends that emerge

And to use the knowledge form those patterns and trends in coming up with a general solution

Solving Problems (3)

It helps if we have experienced that problem or similar ones before

Generally, there are many ways of solving a given problem; the best problem-solvers come-up with the

most appropriate solution more often than not!

The process that can be used to solve a problem is termed as the "algorithm"

Algorithm:

Sequence of steps that can be taken to solve a given problem

sequence

steps

Introduction to Computing CS101

Examples

Addition

Conversion from decimal to binary

The process of boiling an egg

The process of mailing a letter

Sorting

Searching

Let us write down the algorithm for a problem that is familiar to us

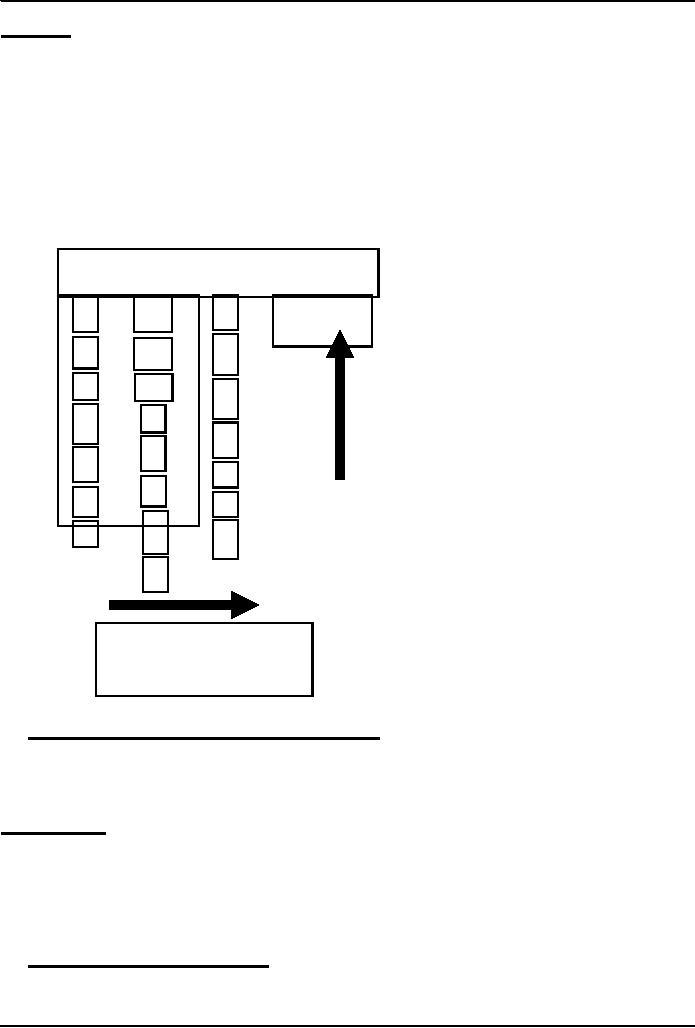
Converting a decimal number into binary

Convert 75 to Binary

remainder

1001011

16.1 Algorithm for Decimal-to-Binary Conversion

Write the decimal number

Divide by 2; write quotient and remainder

Repeat step 2 on the quotient; keep on repeating until the quotient becomes zero

Write all remainder digits in the reverse order (last remainder first) to form the final result

Points to Note:

The process consists of repeated application of simple steps

All steps are unambiguous (clearly defined)

We are capable of doing all those steps

Only a limited no. of steps needs to be taken

Once all those steps are taken according to the prescribed sequence, the required result will be found

Moreover, the process will stop at that point

16.2 Algorithm (Better Definition)

1 Definition:

Sequence of steps that can be taken to solve a problem

Better Definition:

Introduction to Computing CS101

A precise sequence of a limited number of unambiguous, executable steps that terminates in the

form of a solution

Three Requirements:

Sequence is:

Precise

Consists of a limited number of steps

Each step is:

Unambiguous

Executable

The sequence of steps terminates in the form of a solution

16.3 Why Algorithms are Useful?

Once we find an algorithm for solving a problem, we do not need to re-discover it the next time we are

faced with that problem

Once an algorithm is known, the task of solving the problem reduces to following (almost blindly and

without thinking) the instructions precisely

All the knowledge required for solving the problem is present in the algorithm

Why Write an Algorithm Down?

For your own use in the future, so that you don't have spend the time for rethinking it

Written form is easier to modify and improve

Makes it easy when explaining the process to others

16.4 Analysis of Algorithms

Analysis in the context of algorithms is concerned with predicting the resources that re requires:

Computational time

Memory

Bandwidth

Logic functions

However, Time generally measured in terms of the number of steps required to execute an algorithm -

is the resource of most interest

By analyzing several candidate algorithms, the most efficient one(s) can be identified

Selecting Among Algorithms

When choosing among competing, successful solutions to a problem, choose the one which is the least

complex

This principle is called the "Ockham's Razor," after William of Ockham - famous 13-th century English

philosopher

Early History:

Search for a Generic Algorithm

The study of algorithms began with mathematicians and was a significant area of work in the early

years

The goal of those early studies was to find a single, general algorithm that could solve all problems of a

single type

Origin of the Term "Algorithm"

The name derives from the title of a Latin book: Algoritmi de numero Indorum

That book was a translation of an Arabic book: Al-Khwarizmi Concerning the Hindu Art of Reckoning

That book was written by the famous 9-th century Muslim mathematician, Muhammad ibn Musa al-

Khwarizmi

16.5 Al-Khwarzmi

Al-Khwarizmi lived in Baghdad, where he worked at the Dar al-Hikma

Dar al-Hikma acquired and translated books on science and philosophy, particularly those in Greek, as

well as publishing original research

The word Algebra has its origins in the title of another Latin book which was a translation of yet another

book written by Al-Khwarzmi:

Introduction to Computing CS101

Kitab al-Mukhtasar fi Hisab al-Jabr wa'l-Muqabala

Al-Khwarizmi's Golden Principle

All complex problems can be and must be solved

using the following simple steps:

Break down the problem into small, simple sub-problems

Arrange the sub-problems in such an order that each of them can be solved without effecting any other

Solve them separately, in the correct order

Combine the solutions of the sub-problems to form the solution of the original problem

That was some info on history.

Now, let us to take a look at several types of algorithms & algorithmic strategies

16.6 Greedy Algorithm

An algorithm that always takes the best immediate, or local solution while finding an answer

Greedy algorithms may find the overall or globally optimal solution for some optimization problems,

but may find less-than-optimal solutions for some instances of other problems

KEY ADVANTAGE: Greedy algorithms are usually faster, since they don't consider the details of

possible alternatives

Greedy Algorithm: Counter Example

During one of the international cricket tournaments, one of the teams intentionally lost a match, so that

they could qualify for the next round

If they had won that particular match, some other team would have qualified

This is an example of a non-greedy algorithm

Greedy Algorithm: Example

A skier skiing downhill on a mountain wants to get to the bottom as quickly as possible

What sort of an algorithm should the skier be using?

The greedy-algorithm approach will be to always have the skies pointed towards the largest downhill

slope (dy/dx), at all times

What is the problem with that approach?

In what situations that will be the best algorithm?

In which situations would it perform poorly?

16.7 Deterministic Algorithm (1)

An algorithm whose behavior can be completely predicted from the inputs

That is, each time a certain set of input is presented, the algorithm gives the same results as any other

time the set of input is presented.

16.8 Randomized Algorithm (1)

Any algorithm whose behavior is not only determined by the input, but also values produced by a

random number generator

These algorithms are often simpler and more efficient than deterministic algorithms for the same

problem

Simpler algorithms have the advantages of being easier to analyze and implement.

16.9 Randomized Algorithm (2)

These algorithm work for all practical purposes but have a theoretical chance of being wrong:

Either in the form of incorrect results

Or in the form of impractically long running time

Example: Monte Carlo algorithms.

Introduction to Computing CS101

16.10 Deterministic Algorithm (2)

There can be degrees of deterministic behavior: an algorithm that also uses a random number generator

might not be considered deterministic

However, if the "random numbers" come from a pseudo-random number generator, the behavior may be

deterministic

Most computing environments offer a "pseudo random number generators," therefore, most randomized

algorithms, in practice, behave deterministically!

16.11 Heuristic

A procedure that usually, but not always, works or that gives nearly the right answer

Some problems, such as the traveling salesman problem, take far too long to compute an exact, optimal

solution. A few good heuristics have been devised that are fast and find a near-optimal solution more

often than not

Is a heuristic, an algorithm? Yes? No? Why?

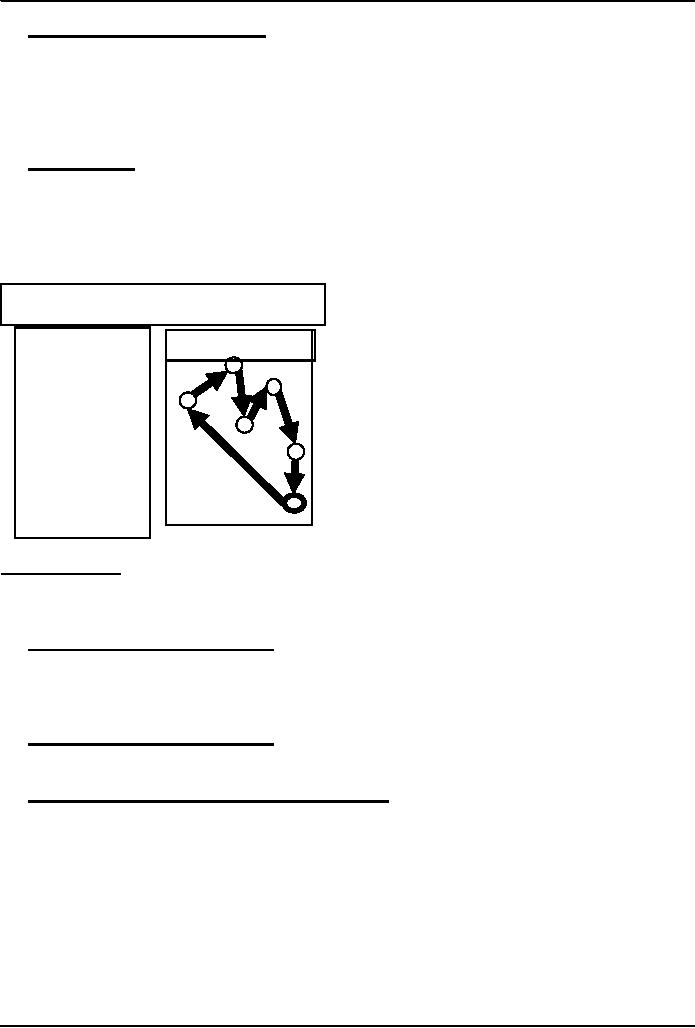
The Traveling Salesman Problem

A salesman needs

A possible sequence for n =

to visit each of the n

cities one after the

other and wants to

finish the trip where

it was started

Determine the

sequence of cities

such that the

traveling distance is

minimized

A Few Questions

Is that the best possible sequence?

How do you know?

How do I determine the best sequence?

16.12 The Brute Force Strategy (1)

A strategy in which all possible combinations are examined and the best among them is selected

What is the problem with this approach?

A: Doesn't scale well with the size of the problem

How many possible city sequences for n=6? For n=60? For n=600?

16.13 The Brute Force Strategy (2)

However, with the relentless increase in computing power, certain problems that only a few years ago

- were impossible to solve with brute force, are now solvable with this technique

16.14 A Selection of Algorithmic Application Areas

Sort

Cryptography

Parallel

Numeric

Graphical

Quantum computing

Combinatory

We'll now talk about the various ways of representing algorithms.

But, before we do that please allow me to say a few words about ...

Introduction to Computing CS101

Syntax & Semantics

An algo. is "correct" if its:

WARNINGS:

1. An algo. can be

Semantics are

syntactically correct, yet

correct

semantically incorrect

very dangerous

situation!

Syntax is correct

2. Syntactic correctness

Semantics:

is easier to check as

The concept embedded in

compared with semantic

an algorithm (the soul!)

Syntax:

The actual representation

of an algorithm (the body!)

Now onto Algorithm Representation

We have said enough about algorithms their definition, their types, etc.

But, how do we actually represent them?

Generally, SW developers represent them in one of three forms:

Pseudo code

Flowcharts

Actual code

Pseudo Code

Language that is typically used for writing algorithms

Similar to a programming language, but not as rigid

The method of expression most suitable for a given situation is used:

At times, plain English

At others, a programming language like syntax

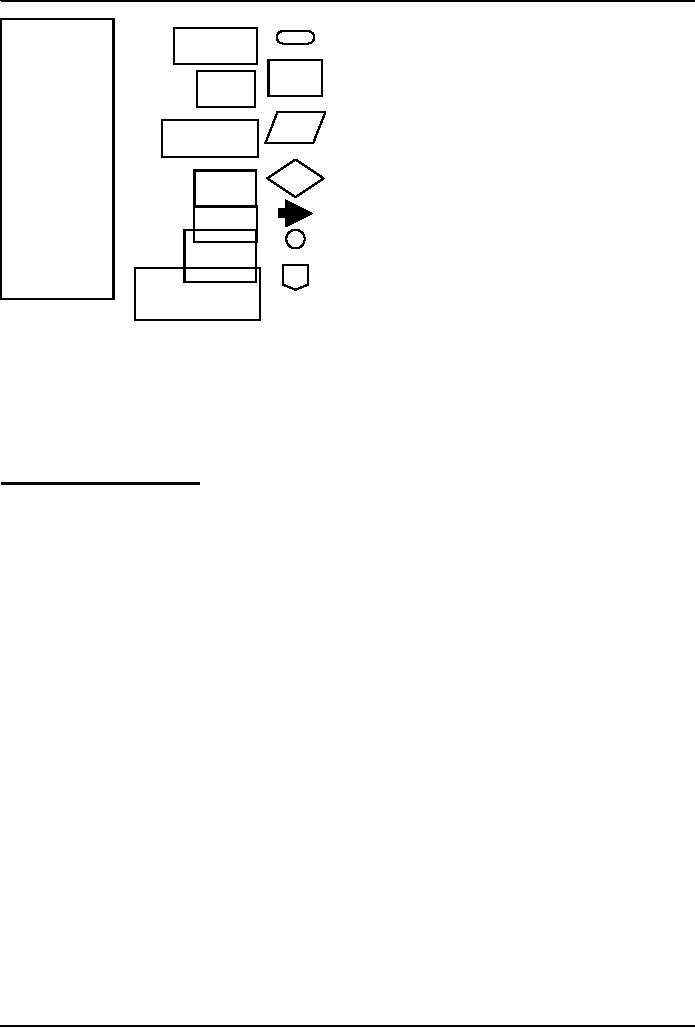
16.15 Flowchart

A graphical representation of a process (e.g. an algorithm), in which graphic objects are used to indicate

the steps & decisions that are taken as the process moves along from start to finish

Individual steps are represented by boxes and other shapes on the flowchart, with arrows between those

shapes indicating the order in which the steps are taken

Introduction to Computing CS101

Flowchart

Start or stop

Elements

Process

Input or output

Decision

Flow line

Connector

Off-page connector

In Today's Lecture, We ...

Became familiar with the concept of algorithms:

What they are?

What is their use?

What do they consist of?

What are the techniques used for representing them?

Next Lecture: Algorithms II

We will continue our discussion on algorithms during the next lecture

In particular, we will discuss the pseudo code and flowcharts for particular problems

We will also discuss the pros and cons of these two algorithm representation techniques i.e. pseudo code

and flow charts

Table of Contents: