Overflow, Implementations of the adder, Unsigned and Signed Multiplication

<< Arithmetic Logic Shift Unit - ALSU, Radix Conversion, Fixed Point Numbers

NxN Crossbar Design for Barrel Rotator, IEEE Floating-Point, Addition, Subtraction, Multiplication, Division >>

Advanced Computer Architecture-CS501

________________________________________________________

Advanced Computer Architecture

Lecture No. 35

Reading Material

Vincent P. Heuring & Harry F. Jordan

Chapter 6

Computer Systems Design and Architecture

6.3, 6.4

Summary

Overflow

Different Implementations of the adder

Unsigned and Signed Multiplication

Integer and Fraction Division

Branch Architecture

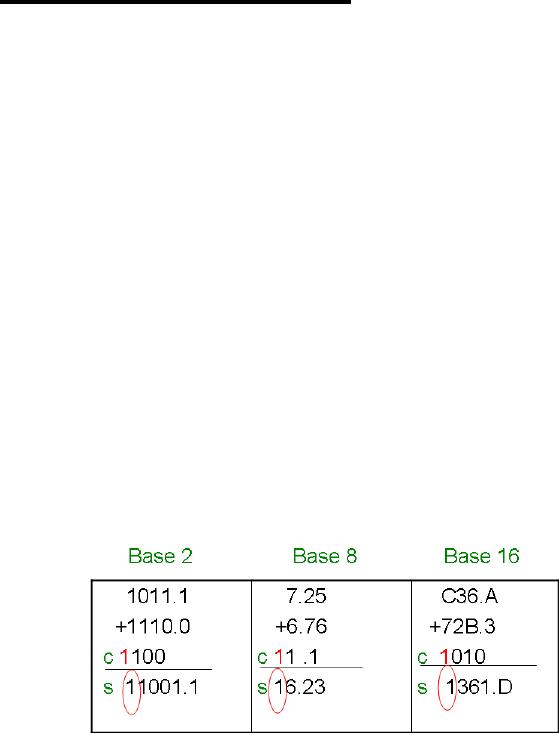
Overflow

When two m-bit numbers are added and the result exceeds the capacity of an m-bit

destination, this situation is called an overflow. The following example describes this

condition:

Example 1

Overflow in fixed point addition:

In these three cases, the fifth position is not allowed so this results in an overflow.

Different Implementations of the Adder

For a binary adder, the sum bit is obtained by following equation:

__ _ _ __

sj = xjyjcj+xjyjcj+xjyjcj+xjyjcj

and the equation for carry bit is

cj+1=xjyj+xjcj+yjcj

where x and y are the input bits.

Page 334

Last Modified: 01-Nov-06

Advanced Computer Architecture-CS501

________________________________________________________

The sum can be computed by the two methods:

Ripple Carry Adder

Carry Look ahead Adder

Ripple Carry Adder

In this adder circuit, we feed carry out from the previous stage to the next stage and so

on. For 64 bit addition, 126 logic levels are required between the input and output bits.

The logic levels can be reduced by using a higher base (Base 16). This is a relatively slow

process.

Complement Adder/Subtractor

We can perform subtraction using an unsigned adder by

· Complement the second input

· Supply overflow detection hardware

2's Complement Adder/Subtractor

A combined adder/subtractor can be built using a mux to select the second adder input. In

this case, the mux also determines the carry-in to the adder. The equation for mux output

is :

_ _

qj =y j r + yj r

Carry Look ahead Adder

The basic idea in carry look ahead is to speed up the ripple carry by determining whether

the carry is generated at the j position after addition, regardless of the carry-in at that

stage or the carry is propagated from input to output in the digit.

This results in faster addition and lesser propagation delay of the carry bits. It divides the

carry into two logical variables Gj (generate) and Pj (propagate). These variables are

defined as:

Gj = xjyj

P j = x j +y j

Hence the carry out will be

c j +1= G j +P j c j

Here the G and P each require one gate, and the sum bit needs two more gates in the full

adder. This results in a less complexity i.e. log(m) which is much less as compare to

ripple carry adder where complexity is m (m is the number of bits of a digit to be added).

Ripple carry and look ahead schemes are can be mixed by producing a carry-out at the

left end of each look ahead module and using ripple carry to connect modules at any level

of the look ahead tree.

Unsigned Multiplication

The general schema for unsigned multiplication in base b is shown in Figure 6.5 of the

text book.

Page 335

Last Modified: 01-Nov-06

Advanced Computer Architecture-CS501

________________________________________________________

Parallel Array Multiplier

Figure 6.6 of the text book shows the structure of a fully parallel array multiplier for base

b integers. All signal lines carry base b digits and each computational block consists of a

full adder with an AND gate to form the product xiyj. In case of binary, m2 full adders are

required and the signals will have to pass through almost 4m gates.

Series parallel Multiplier

A combination of parallel and sequential hardware is used to build a multiplier. This

results in a good speed of operation and also saves the hardware.

Signed Multiplication

The sign of a product is easily computed from the sign of the multiplier and the

multiplicand. The product will be positive if both have same sign and negative if both

have different sign. Also, when two unsigned digits having m and n bits respectively are

multiplied, this results in a (m+n) bit product, and (m+n+1)-bit product in case of sign

digits. There are three methods for the multiplication of sign digits:

1. 2's complement multiplier

2. Booth recoding

3. Bit-Pair recoding

2's complement Multiplication

If numbers are represented in 2's complement form then the following three

modifications are required:

1. Provision for sign extension

2. Overflow prevention

3. Subtraction as well as addition of the partial product

Booth Recoding

The Booth Algorithm makes multiplication simple to implement at hardware level and

speed up the procedure. This procedure is as follows:

1. Start with LSB and for each 0 of the original number, place a 0 in the recorded

number until a 1 in indicated.

2. Place a 1 for 1in the recorded table and skip any succeeding 1's until a 0 is

encountered.

3. Place a 0 with 1 and repeat the procedure.

Example 2

Recode the integer 485 according to Booth procedure.

Page 336

Last Modified: 01-Nov-06

Advanced Computer Architecture-CS501

________________________________________________________

Solution

Original number:

00111100101=256+128+64+32+4+1=485

Recoded Number:

_ _ _

01000101111=+512-32+8-4+2-1=485

Bit-Pair Recoding

Booth recoding may increase the number of additions due to the number of isolated 1s.

To avoid this, bit-pair recoding is used. In bit-pair recoding, bits are encoded in pairs so

there are only n/2 additions instead of n.

Division

There are two types of division:

Integer division

Fraction division

Integer division

The following steps are used for integer division:

1. Clear upper half of dividend register and put dividend in lower half. Initialize

quotient counter bit to 0

2. Shift dividend register left 1 bit

3. If difference is +ve, put it into upper half of dividend and shift 1 into quotient. If

ve, shift 0 into quotient

4. If quotient bits<m, goto step 2

5. m-bit quotient is in quotient register and m-bit remainder is in upper half of

dividend register

Example 3

Divide 4710 by 510.

Solution

D=000000 101111,

d=000101

000001 011110

000101

Diff(-)

000010 111100

Page 337

Last Modified: 01-Nov-06

Advanced Computer Architecture-CS501

________________________________________________________

000101

Diff(-)

000101 111000

000101

Diff(+)

001

000001 110000

000101

Diff(-)

0010

000011 100000

000101

Diff(-)

00100

000111 000000

000101

Diff(+)000010

001001

Hence remainder = (000010)2 = 210

Quotient = (001001)2 = 910

Fraction Division

The following steps are used for fractional division:

1. Clear lower half of dividend register and put dividend in upper half. Initialize

quotient counter bit to 0

2. If difference is +ve, report overflow

3. Shift dividend register left 1 bit

4. If difference is +ve, put it into upper half of dividend and shift 1 into quotient. If

negative, shift 0 into quotient

5. If quotient bits<m, go to step 3

6. m-bit quotient has decimal at the left end and remainder is in upper half of

dividend register

Branch Architecture

The next important function perform by the ALU is branch. Branch architecture of a

machine is based on

1. condition codes

2. conditional branches

Condition Codes

Condition Codes are computed by the ALU and stored in processor status register. The

`comparison' and `branching' are treated as two separate operations. This approach is not

used in the SRC. Table 6.6 of the text book shows the condition codes after subtraction,

for signed and unsigned x and y. Also see the SRC Approach from text book.

Page 338

Last Modified: 01-Nov-06

Advanced Computer Architecture-CS501

________________________________________________________

Usually implementation with flags is easier however it requires status registers. In case of

branch instructions, decision is based on the branch itself.

Note: For more information on this topic, please see chapter 6 of the text book.

Page 339

Last Modified: 01-Nov-06

Table of Contents: